A curious number exploration
Posted by: Gary Ernest Davis on: May 6, 2011
Benjamin Vitale (@BenVitale) tweeted that he followed 203 people on Twitter and is a prime number.
Alex Bogomolny (@CutTheKnotMath) observed that if (digits base 10) then
has a factor of
unless one of
.
A quick computational search (using Mathematicaâ„¢) yields the following numbers (base 10 digits) for which
is prime:
10, 20, 203, 230, 308, 309, 330, 350, 503, 603, 650, 960, 1068, 1110, 1206, 1350, 1404, 1480, 1730, 1802, 1860, 1910, 2032, 2038, 2044, 2054, 2250, 2320, 2502, 3044, 3082, 3402, 3970, 4032, 4046, 4072, 4120, 4340, 4450, 4540, 4650, 4908, 5204, 5310, 5402, 5530, 5770, 5820, 6038, 6076, 6120, 6206, 6490, 6520, 6830, 7110, 8074, 8106, 8120, 8380, 8450, 8610, 8690, 8902, 8960, 9064, 9330, 9402, 9408, 9950
How do these numbers increase?
Are they becoming relatively rarer?
Let’s denote by the number of
such that
 is prime.
How does the fraction vary with increasing
?
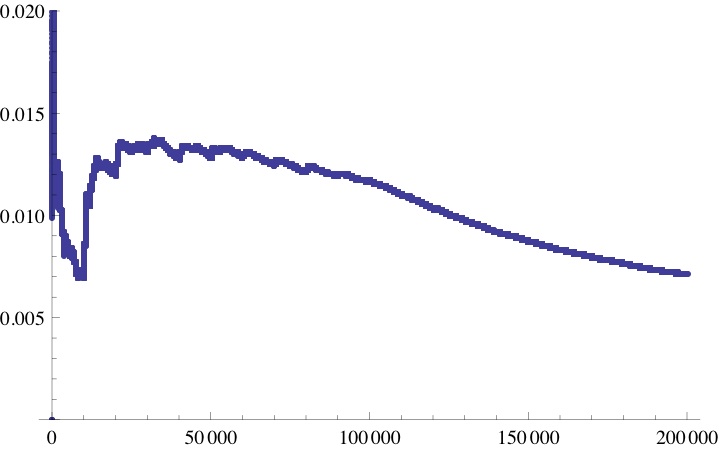
Here is a plot of that fraction up to :
It appears that as
increases, although the decrease is highly exaggerated by the foreshortened plot.
Does as
increases?
Postscript
Matt Henderson (@mattthen2) made the following useful observation:
Let denote the number of
whose digits contain a
.
Then so
for all
.
Because for all
we see that:
for all
.

Leave a Reply