Codes for kids (1): Simple substitution ciphers
The idea of a simple substitution code
Simple substitution ciphers substitute one letter of the alphabet for another, in some random arrangement. Here is an example of a simple substitution cipher:
| A | → | D |
| B | → | V |
| C | → | N |
| D | → | X |
| E | → | I |
| F | → | K |
| G | → | S |
| H | → | W |
| I | → | Y |
| J | → | Z |
| K | → | T |
| L | → | Q |
| M | → | M |
| N | → | H |
| O | → | P |
| P | → | A |
| Q | → | U |
| R | → | F |
| S | → | L |
| T | → | G |
| U | → | E |
| V | → | O |
| W | → | B |
| X | → | C |
| Y | → | R |
| Z | J |
To use this substitution cipher table to write a coded message, substitute each letter in the original message with the substitute letter from the table. For example, the message:
WHO WROTE THIS MESSAGE
would be coded as:
BWP BFPGI GWYL MILLDSI
On the other hand, if someone got the coded message:
BWIFI DFI RPE
they could use the cipher table to decode the message as:
WHERE ARE YOU
Simple substitution ciphers in history and literature
Julius Caesar
Julius Caesar used a simple substitution cipher to send secret messages. His substitution cipher consisted of shifting the letters of the alphabet 3 to the left, with the first 3 letters shifting to the end of the alphabet:
| A | → | X |
| B | → | Y |
| C | → | Z |
| D | → | A |
| E | → | B |
| F | → | C |
| G | → | D |
| H | → | E |
| I | → | F |
| J | → | G |
| K | → | H |
| L | → | I |
| M | → | J |
| N | → | K |
| O | → | L |
| P | → | M |
| Q | → | N |
| R | → | O |
| S | → | P |
| T | → | Q |
| U | → | R |
| V | → | S |
| W | → | T |
| X | → | U |
| Y | → | V |
| Z | → | W |
Sherlock Holmes
In The Adventure of the Dancing Men, by Arthur Conan Doyle, Sherlock Holmes is shown a page from a notebook with the following markings made in pencil:
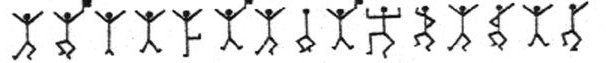 Holmes guesses correctly that this is a simple substitution cipher in which the little dancing figures are substituted for letters of the alphabet. Using his knowledge of how often different letters occur in English Holmes is able to decode the message.
Holmes guesses correctly that this is a simple substitution cipher in which the little dancing figures are substituted for letters of the alphabet. Using his knowledge of how often different letters occur in English Holmes is able to decode the message.
How to produce a simple substitution cipher
A random method
Letters of the alphabet can be chosen at random to make the second column of a simple substitution cipher.
(1) For example, the 26 letters of the alphabet, written on pieces of card, can be placed in a container which is shaken hard, and a letter chosen at random. The first letter chosen substitutes for “A”. That letter is not put back in the container, which is shaken again and a new letter drawn. That letter substitutes for “B”, and so on on.
(2) Another way to produce a random simple substitution cipher is to use a spreadsheet. In a spreadsheet make a column with the letters of the alphabet in order, as shown in the first table above. Then copy that column into an adjoining column in the spreadsheet. In the next column, produce a random decimal number by using the command “=rand()”. Copy this formula down the 26 rows of that column so that all letters have a random decimal number next to them. Now select columns 2 and 3 and sort in order by column 3. This sorts the second column of letters randomly and gives us the second column of the simple substitution cipher.
A shift method
You can construct a simple substitution cipher using Julius Caesar’s method by shifting all the letters of the alphabet along by a fixed amount.
(1) For example in Julius Casar’s simple substitution cipher all letters were shifted to the left by 3, with the 3 letters A, B, C at the beginning if the alphabet shifter to the end: X, Y, Z.
This is like moving the letters 3 spaces anti-clockwise around a circle:
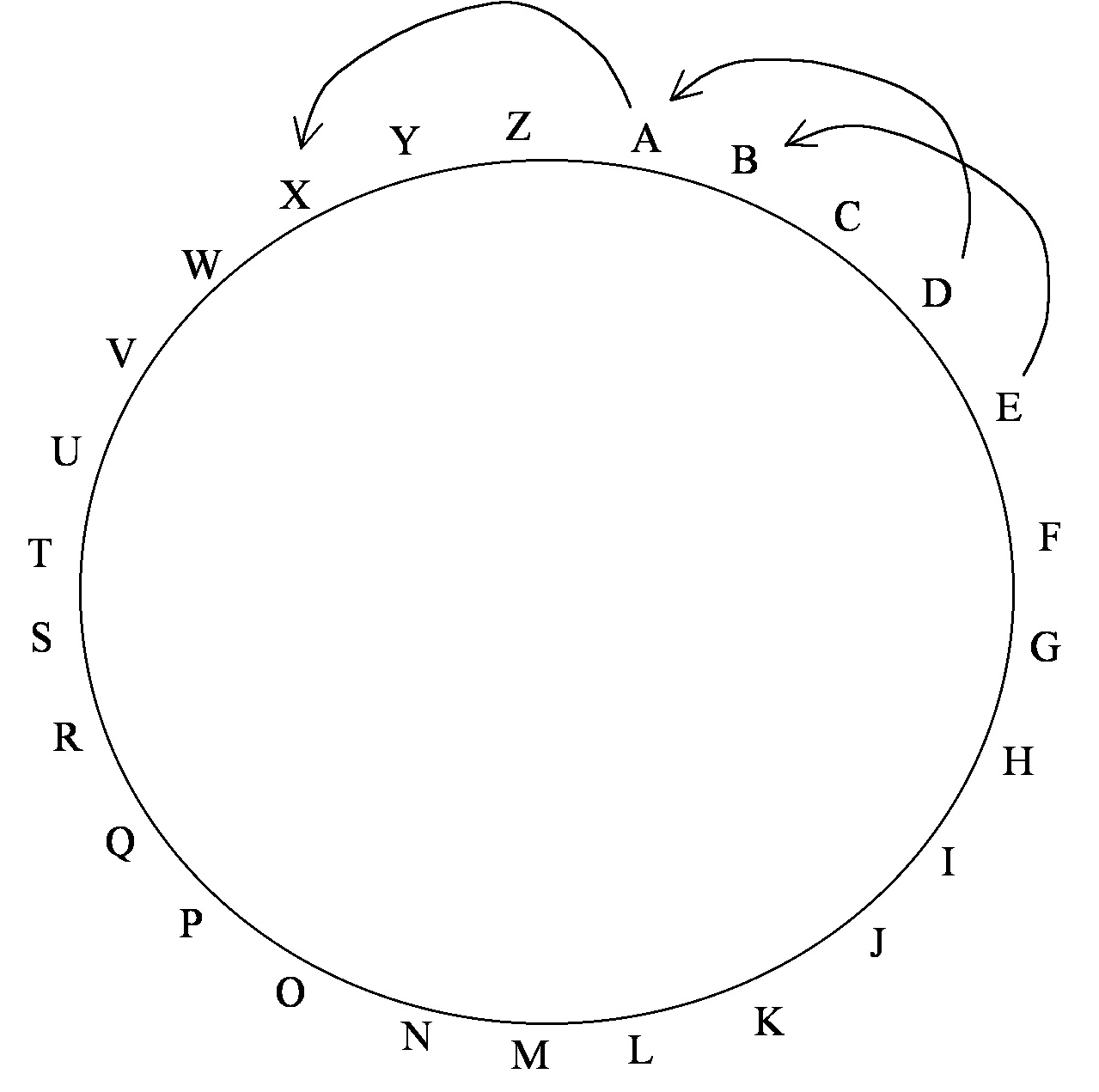 You can use shifts by other amounts.
You can use shifts by other amounts.
(2) Another way to make a shift cipher like this is first to represent all the letters of the alphabet by whole numbers, in order, starting from 0. So A is represented by 0, B by 1, C by 2, and so on through Z by 25.
A shift cipher where every letter is shifted 2 to the right can be made by adding 2 to each number, except that when we get to 26 we subtract 26 from the answer. You can easily do this by hand
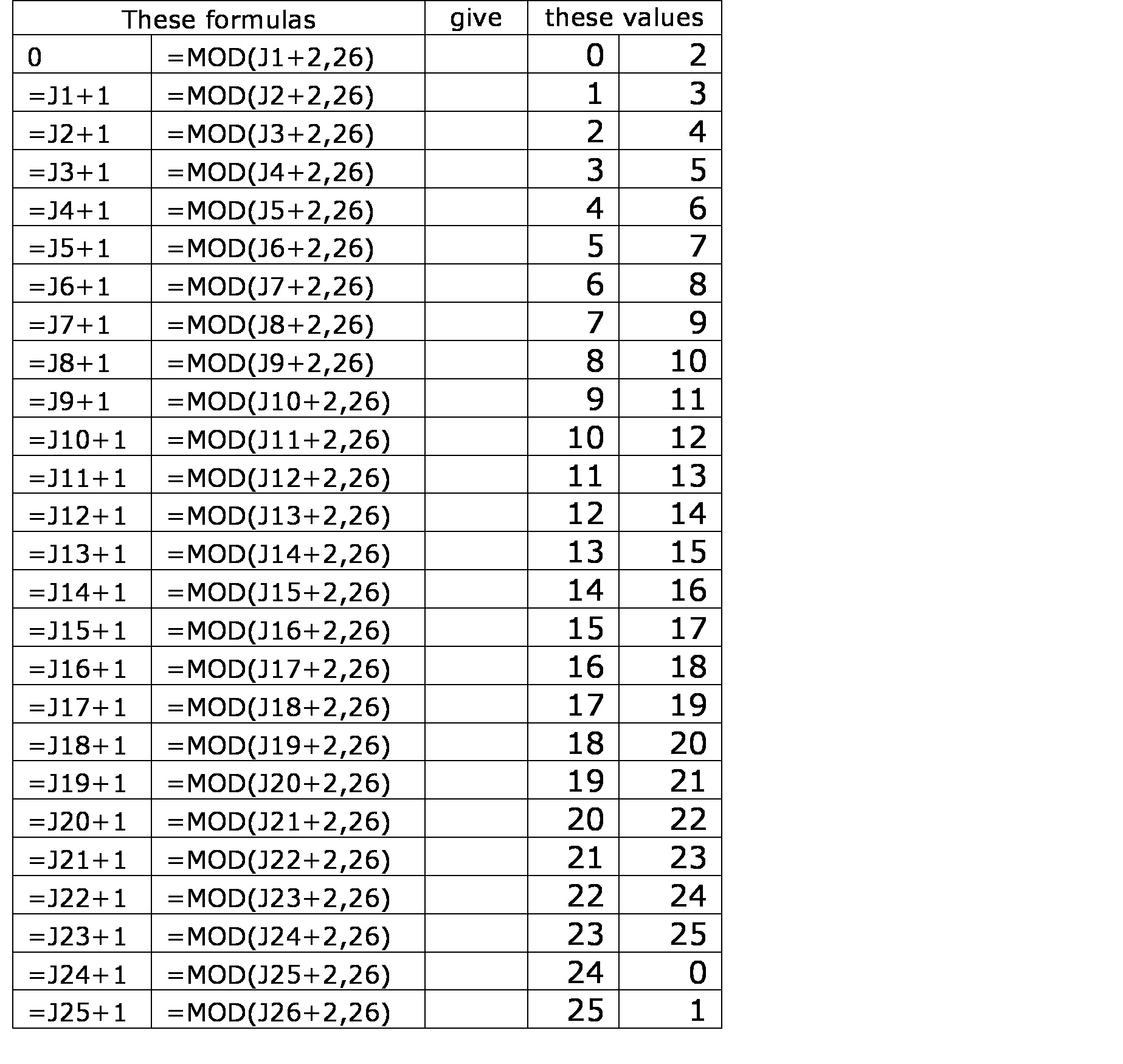
A shift cipher can also be constructed in most spreadsheets, using the “=mod(“number”+2,26)” command. To construct a shift cipher in which all letters – represented by numbers – are shifted 2 to the right, first create a column of the numbers 0 through 26. Do this by putting the number 0 in the first row. In the second row enter a formula to add 1 to the previous number. Then copy that formula down to the 26th row. In the second column enter the “=mod(“number”+2,26)” where “number” points to the first row of the first column. Then copy that formula down to the 26th row.
 How to crack a simple substitution cipher
How to crack a simple substitution cipher
When we know the table for a simple substitution cipher it’s easy to decode a coded message. But if we just have the message and do not know the cipher how can we decode a message. How did Sherlock Holmes crack the code of the dancing men?
If the coded message is very short, and we only have one message it is hard to crack a simple substitution cipher. But if we have a long enough message, or several messages made with the same substitution cipher, then we have a good chance of cracking the code.
We do this by counting how many times each coded letter appears in the message, or messages. How does this help us? It helps because the approximate frequency of letters in English is known. Sherlock Holmes used the following rough guide: E, T, A, O, N, R, I, S, H, D, L, F, C, M, U, G, Y, P, W, B, V, K, X, J, Q, Z. This means that “E” is the most commonly occurring letter in English, with “T” or “A” following next, and so on, with “J, Q, Z” being the least commonly occurring letters.
Let’s say we get the coded message
M MQEKMRI CSX AMPP JMRH MX JEMVPC WMQTPI XS GVEGO XLMW QIWWEKI AVMXXIR E WMQTPI WYFWXMXYXMSR GSHI EJXIV EPP CSY EVI TVIXXC WQEVX WXYHIRXW
and we suspect this was coded by a simple substitution cipher.
The first thing to do is to count how often each letter appears in the message, and arrange the letters in order by frequency of occurrence:
| Frequency | Letter |
| 15 | X |
| 13 | M |
| 11 | I |
| 9 | E |
| 9 | W |
| 7 | P |
| 7 | V |
| 5 | Q |
| 5 | R |
| 5 | S |
| 4 | C |
| 4 | Y |
| 3 | G |
| 3 | H |
| 3 | J |
| 3 | T |
| 2 | A |
| 2 | K |
| 1 | F |
| 1 | L |
| 1 | O |
It’s a fair guess that “X” is code for either “E” or “T”.
Let’s test for a shift cipher.
If “X” is code for “E” then all letters have been shifted 19 to the right – or, what amounts to the same thing 7 to the left. If that’s what happened, then the original message begins FÂ F JXDFK B.
That doesn’t look right, so let’s see if we have a shift cipher in which the letter “X” is replaced by “T”. In this case all letters are shifted 4 to the right. If that’s what happened then the original message begins I IMAGINE YOU … . This looks like it IS what happened and we can easily decode the message.
Other ways of writing a coded message
Even when a message is coded by a simple substitution cipher the shape of words can be a strong clue as to which letters have been substituted, for example a single letter occurring on its own could only be A or I. This is a big clue, so coded messages are usually all run together, like this:
MMQEKMRICSXAMPPJMRHMXJEMVPCWMQTPIXSGVEGOXLMWQIWWEKI AVMXXIREWMQTPIWYFWXMXYXMSRGSHIEJXIVEPPCSYEVITVIXXCWQEVXWXYHIRXW
Sometimes they are broken into fixed length pieces, like this:
MMQ EKM RIC SXA MPP JMR HMX JEM VPC WMQ TPI XSG VEG OXL MWQ IWW EKI Â AVM XXI REW MQT PIW YFW XMX YXM SRG SHI EJX IVE PPC SYE VIT VIX XCW QEV XWX YHI RXW
Other ways of coding
Because simple substitution ciphers are relatively easy to crack, much effort has gone into developing harder to crack ciphers. Some of these are hard for the average person to crack, but relatively easy for people who know enough mathematics. Ciphers are used everyday to code business transactions, including those using debit and credit cards. The ciphers used for these business messages are very hard to crack indeed.
Reading
Top Secret: A Handbook of Codes, Ciphers and Secret Writing. Edited by Paul Janeczko
The Magic of Numbers by Benedict Gross & Joe Harris (this book has two chapters on codes)
In Code: A Mathematical Journey, by Sarah Flannery
The Book of Codes: Understanding the World of Hidden Messages. Edited by Paul Lunde
The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography, by Simon Singh
Learning goals & outcomes
Some things students can be expected to learn by writing and attempting to break simple substitution ciphers:
- How to construct a simple substitution cipher
- Some history of codes
- Systematic counting
- Analyzing data, using informed guess and check
- Working in teams
More advanced:
- Using random numbers to make sorted random lists
- Using arithmetic modulo 26 to make shift ciphers

November 16, 2010 at 11:37 pm
i definitely agree