Factorions, Munchausen numbers, cubions and related things
Posted by: Gary Ernest Davis on: April 28, 2011
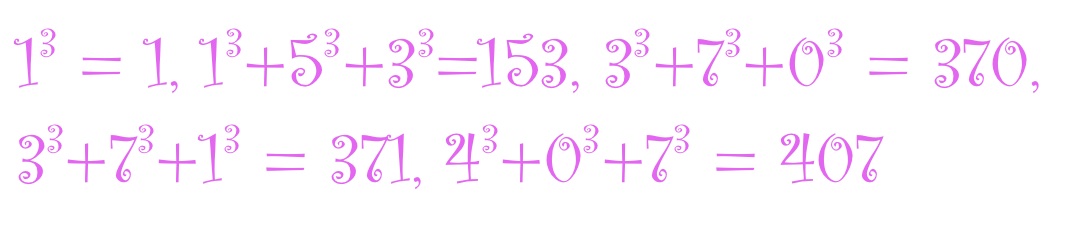 Factorions
Factorions
The four numbers $latex 1, decease 2, treatment 145 extrm{ and } 40585$ have the following peculiar property:
$latex 1!=1, clinic 2!=2, 1!+4!+5!=145 extrm{ and } 4!+0!+5!+8!+5! =40585$.
Numbers that have this property – that the sum of the factorials of their digits equals the number themselves – are called factorions.
It turns out these 4 numbers are the only whole number factorions, a point we will turn to below.
Münchausen numbers
The numbers have the peculiar property that
.
Numbers (base 10 digits) with the property that
are called Münchausen numbers, and dependent on how we define
– either as
– there are 2 or 3 of them.
Cubions
Are there any positive integers (base 10 digits) with the property that
?
Yes: 1, 153, 370, 371, 407 all have this property – we call them cubions – and they are the only positive integer cubions.
F-ions
The three sets of examples above can all be encapsulated as instances of the following general notion.
Let be a function defined on non-negative integers and taking non-negative integer values.
We call a non-negative integer (base 10 digits) an F-ion ifÂ
Factorions correspond to the function , Münchausen numbers to the function
(with an appropriate choice of
), and cubions to the function
.
Notation: for (base 10 digits) we will denote
by
Bounds on the number of F-ions
We will see that for any function the size of F-ions is bounded by an number that we can calculate numerically.
This allows us to conclude that for such the number of F-ions is finite.
Moreover, because we can numerically calculate the bound, we can do a computational search up to that bound to see if we have found all F-ions.
1. The number of digits of a positive integer
For a positive integer the number of (base 10) digits of
is the floor of
, the largest integer less than or equal to
.
This means that the number of digits of is less than
.
2. An inequality for ![n^{[F]}](http://s0.wp.com/latex.php?latex=n%5E%7B%5BF%5D%7D&bg=ffffff&fg=8E8778&s=0&c=20201002)
If the base 10 digits of the positive integer are
then:
for
- The number of digits of
is
Let
Then we have:
This says that cannot grow too big in terms of the number of digits of
.
3. An inequality for large 
We look at the behavior of the function :
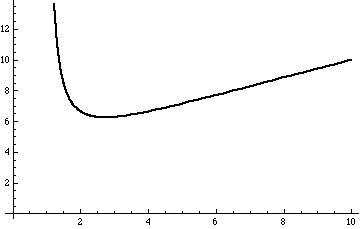
Graph of x/log10(x) for x>1
The derivative of is
and this is positive for
so for
the function
is strictly increasing.
Therefore there is a smallest non-negative integer for which
.
For we have
and so
.
So, for we cannot have
, so showing that the number of F-ions is finite.
Finding a solution to 
The least non-negative integer for which
is the ceiling of the unique solution
to
.
There are a number of ways to estimate the solution to
.
One way, using Mathematica, is:
> FindRoot[x/Log[10, x] == A, {x, substitute guesstimate for x*}]
For example, to get an upper bound for cubions, where we first calculate
and guesstimate from a graph of
that
:
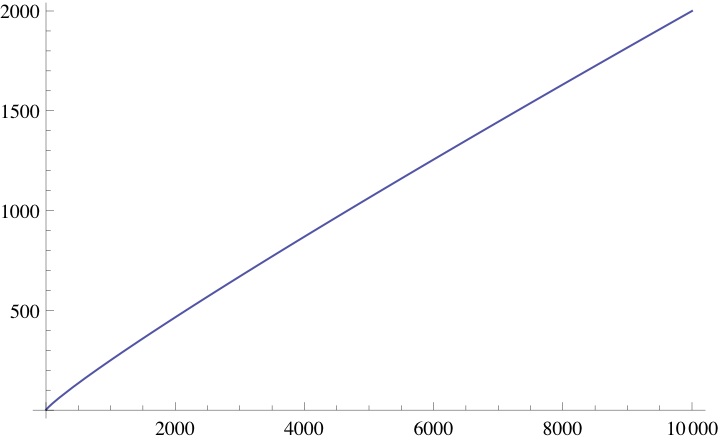
The Mathematica code:
FindRoot[x/Log[10, x] == 9^3, {x, 3000}]
gives so
.
The positive cubions we found were 1, 153, 370, 371, 407 and an easy check up to shows there are no others.
Squarions
A squarion is a positive integer for which
where
.
There are no positive squarions other than 1.
The argument above show that there are none greater than 184, and a simple check shows that 1 is the only squarion below 184.
Further thoughts
This result applies to any function defined for non-negative integers and taking non-negative integer values, including such weird functions as the following:Â
:
Only are F-ions for this choice of
.
Acknowledgements
Thanks to Alexander Bogomolny for helpful discussions.
van Berkel, D. (2009) On a curious property of 3435. Retrieved from arxiv.org: On_a_curious_property_of_3435 [This article provides the argument I have described in this post]
2 Responses to "Factorions, Munchausen numbers, cubions and related things"
It should not come as a surprise that I liked your post.
I also though about generalizing the Munchausen numbers and came up with the same conclusions as that you demonstrated in this post.
It did get my thinking on the following question: what function would produce the most F-ions? In order to compare different function “honestly” one should normalize the count by dividing by the smallest upper bound.

September 2, 2013 at 11:43 am
What happens if you replace base ten with something different: eg factorial representation? Presumably it might be possible then to find F for which there are infinitely many F-ions?