Republic of Mathematics blog

Fibonacci tricks from Palm Breeze CAFE

Posted by: Gary Ernest Davis on: November 17, 2010

Tweet
Share
Pin
Share
0 Shares

Here’s the algebra:

x

x

x

x

x

x

x

More generally, if F(n) is the n^{th} Fibonacci number, where F(1)=A, F(2)=B \textrm{ and } F(n+2)=F(n+1)+F(n), and S(n) is the sum of the Fibonacci numbers F(1)+\ldots+F(n) then S(6+4k)  is an integer multiple of F(5+2k).

For example, S(14)=F(1)+\ldots+F(14)=29\times F(9), and S(98)=F(1)+\ldots+F(98)=17393796001\times F(51).

1 Response to "Fibonacci tricks from Palm Breeze CAFE"

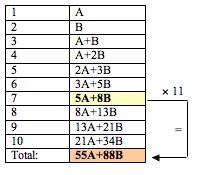
1 | Fibonacci Sequences – the Golden Rule about the Golden Ratio, which we just found out… « Teaching AQA GCSE Maths 2010
November 18, 2010 at 12:16 pm

[…] Our thanks to the Republic of Maths blog that brought this to our attention, via this video link. […]

Leave a Reply

Visitor map

Locations of visitors to this page

Get a free blog at WordPress.com

Theme: Albeo by Design Disease.