Differential equations and studio learning

This semester I am once again teaching introductory differential equations.

The students in this class are mainly engineering majors, with some mathematics and physics majors, for whom the course is mandatory. Occasionally a humanities or business major will enroll in this class for interest, but not this semester.

The computer laboratory where the class meets has 16 computers, each shared by two students, so the maximum class enrollment is 32.  Of those 32 most are young – usually sophomore – males, but this semester there are 6 females: 5 engineering majors and 1 mathematics major.

I run this course as a studio class in which students have projects to work on in pairs. Projects last from 2-3 weeks, and all work in progress and final reports must be placed on WordPress blogs. A class list with active links to individual student blogs allows all students to readily see all other student work.

After completion of a project I write critiques on individual student blogs, together with a putative grade for each student. Students may revise earlier projects and ask me to regrade them (If, however, they submit nothing by the due date they receive zero for that project).

Students are advised in writing, and in periodic class announcements, of the University policy on plagiarism, and of the need to make all written work their own. Naturally, students who work for 6 or so classes at the same computer, doing and discussing the same calculations, will have a lot in common to write about. They must, however, tell their own story in their own words. This also means avoiding lengthy quotes from other students, in lieu of writing their own thoughts and conclusions.
I was experimenting with this approach to teaching and learning some time before I came across John Seely Brown’s excellent account of the effects of studio-style teaching on student learning:

Learning to see

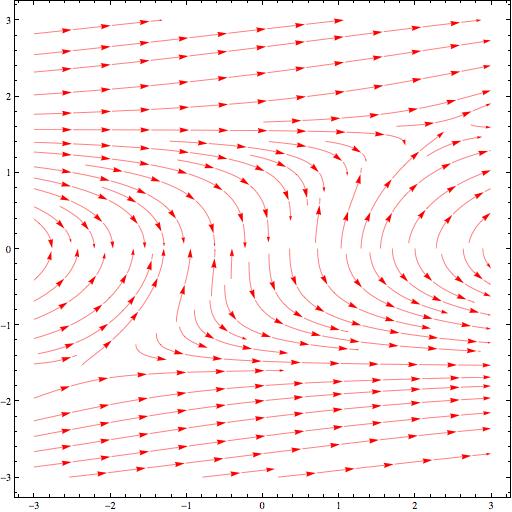
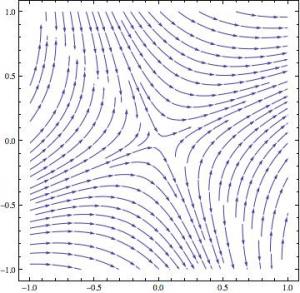
The first thing I have the students do is plot vector fields of differential equations and to examine those plots for characteristic features.

I use Mathematica for this purpose because it is more widely available in the Universty than MATLAB or Maple, and also, in my view, produces better graphics (that, of course, is an arguable point). Mathematica has a streamplot option which draws candidate integral curves of a differential equations, and so allows a student to be able to better see what potential solution curves look like.

This, to my mind, is somewhat like looking at paintings in an art history course – learning to see more deeply.

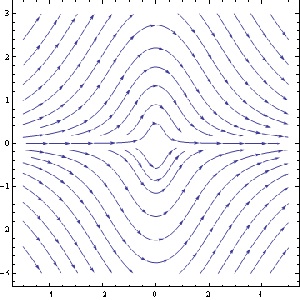
Here’s a couple of examples where the students have some difficulty putting what they think they see into words:

A couple of students discussed what appear to be hyperbolic forms in the first example, and quite a few more discussed the appearance of asymptotes. Many more, however, described the plot as being composed of a bunch or parabolas.

We can imagine what’s going on in their minds here: they are clutching at words that sound appropriate, words such as “parabola” for something generally curved.

The first thing I wanted them to do, however, was to look into the plot and tell me what they saw.

Of course, looking is not just an act of having light hit one’s eyeballs: it is an active process of interpreting what is in front of one’s eyes, and an active process of seeking out finer, previously unnoticed, details. It is, in other words, an intelligent process.

This, is quite unlike anything these students have encountered before in a mathematics class.

Previous mathematics classes have been about doing calculations, solving problems, or trying to construct proofs.

No one in their prior experience has asked them to look at a relatively complicated mathematical plot and  describe in depth and detail what they saw.

But, of course, if vector plots of differential equations are to be useful to the practicing engineer, mathematician and scientist (and they are) then those professionals must be able to look deeply and interpret what the machine has produced.

The striking symmetry in the second plot was mentioned by only one student, and then not fully. Only one student mentioned that the solution curves approach 0 at and reach a maximum (or minimum, respectively) at .

There was a lot going on in these first two weeks that students had to get used to: working in pairs with other students they did not know, learning to use WordPress and write LaTeX, and learning to use Mathematica, and get the graphics output in jpeg format t o upload to WordPress.

It’s understandable they thought the main task was to get something done, and that something was to produce nice vector plots.

It’s taking them some time to understand that my main focus is on looking deeply into what the plots tell us.

Learning to think

Only one of the 32 students attempted to predict, from the form of a differential equation, what the solution curves might look like:

“So if you look at this function analytically I suppose any time x=y the function equals zero because the argument in the numerator is (x-y) and subtracting equal values gives you zero. In the denominator I would expect an asymptote if y=-x because summing them would create a zero in the denominator and making the function undefined.”

To be fair, I did not say in writing that students should relate features of the differential equation to likely solution curves, or having seen the streamline plot, say what aspects of the solution curves correspond to what features of the differential equations. But I did say this verbally in class on several occasions, and did talk about it in depth with several groups of students.

Overall, I am not unhappy. The students are moving more slowly than I hoped for and would like. But they have got things working, and even though there is another topic and project now well under way, they have a chance to go back and to take time to look again at their plots and see how features of the differential equation are reflected in features of the plots.

They have a chance, in other words, to look, to see, to think, and to learn.

Can this really be mathematics? they ask.