Happy mathematical new year: 2011 scores again (so does 2012, coming up in under a year)
Posted by: Gary Ernest Davis on: January 11, 2011
In a previous post I discussed how 2011 is a prime number and also a sum of consecutive prime numbers.
2011 has another curious property that it shares with 2012, and with 2001 and 2002:
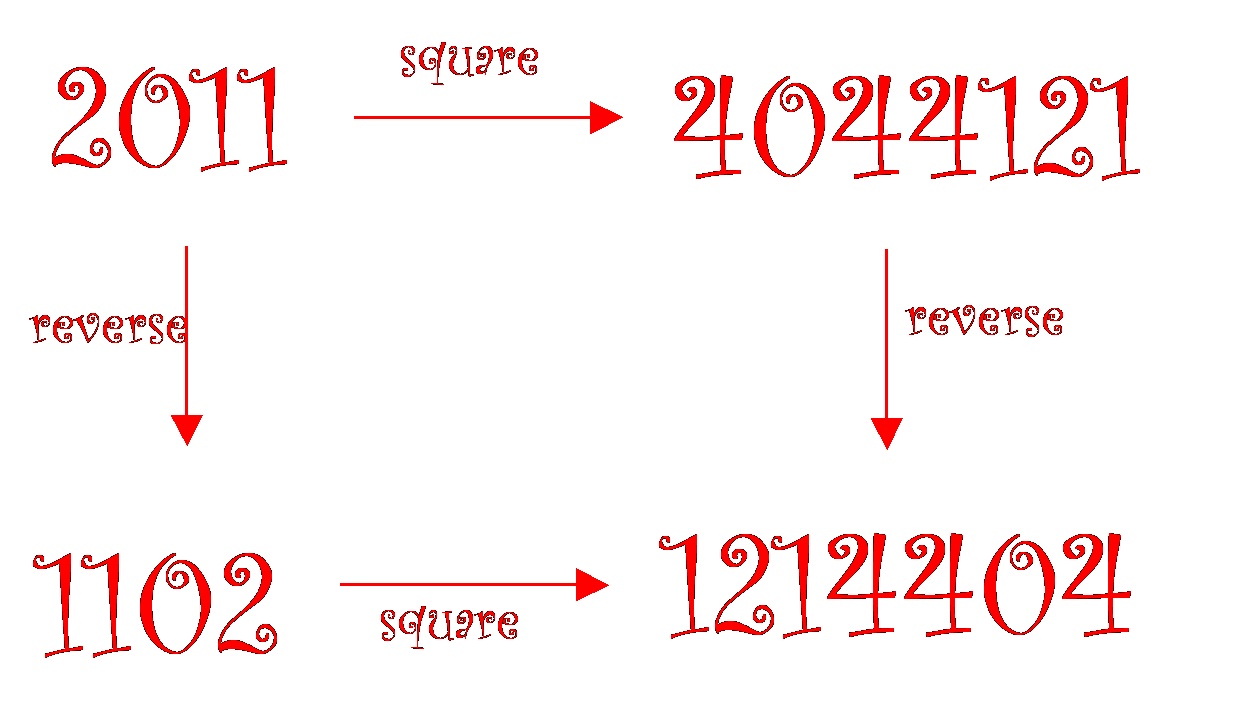
- Reversing the digits of 2011 we get the number 1102
- Squaring 1102 gives us the number 1214404.
- On the other hand, squaring 2011 gives us the number 4044121, and reversing the digits of that number also gives us 1214404.
In other words, 2011 is a number for which the operations “reversing the digits” and “squaring” commute: it does not matter which order we do these operations, we get the same answer.
This is exemplified in the following commutative diagram:
What other numbers have this property?
Here’s a list of a few:
1, 2, 3, 11, 12, 13, 21, 22, 31, 101, 102, 103, 111, 112, 113, 121,122, 201, 202, 211, 212, 221, 301, 311, 1001, 1002, 1003, 1011, 1012, 1013, 1021, 1022, 1031, 1101, 1102, 1103, 1111, 1112, 1113, 1121, 1122, 1201, 1202, 1211, 1212, 1301, 2001, 2002, 2011, 2012, 2021,2022, 2101, 2102, 2111, 2121, 2201, 2202, 2211
This feels like it would be a fun exploration for middle school kids.
I used Mathematicaâ„¢ to do the search, but school students could use Excel
My Mathematicaâ„¢ code was:
func[n_]:=
Sqrt[FromDigits[Reverse[IntegerDigits[
FromDigits[Reverse[IntegerDigits[n]]]^2]]]];
L={};
Do[
If[func[n]==n,L=Append[L,n]],
{n,1,3000}]
L
5 Responses to "Happy mathematical new year: 2011 scores again (so does 2012, coming up in under a year)"
January 11, 2011 at 2:47 pm
This made me wonder how often this occurs. For the years 1000 through 9999:
>>> [year for year in range(1001,10000) if square(reverse(year)) == reverse(square(year))]
[1001, 1002, 1003, 1010, 1011, 1012, 1013, 1020, 1021, 1022, 1030, 1031, 1100, 1101, 1102, 1103, 1110, 1111, 1112, 1113, 1120, 1121, 1122, 1130, 1200, 1201, 1202, 1210, 1211, 1212, 1220, 1300, 1301, 2000, 2001, 2002, 2010, 2011, 2012, 2020, 2021, 2022, 2100, 2101, 2102, 2110, 2111, 2120, 2121, 2200, 2201, 2202, 2210, 2211, 3000, 3001, 3010, 3011, 3100, 3101, 3110, 3111]
(Done in Python)
Interesting, nothing beyond 3111!
January 11, 2011 at 4:06 pm
Michel,
beyond 10,000 I found:
10001 , 10002 , 10003 , 10011 , 10012 , 10013 , 10021 , 10022 ,
10031 , 10101 , 10102 , 10103 , 10111 , 10112 , 10113 , 10121 ,
10122 , 10201 , 10202 , 10211 , 10212 , 10221 , 11001 , 11002 ,
11003 , 11011 , 11012 , 11013 , 11021 , 11022 , 11031 , 11101 ,
11102 , 11103 , 11111 , 11112 , 11113 , 11121 , 11122 , 11201 ,
11202 , 11211 , 12001 , 12002 , 12011 , 12012 , 12101 , 12102 ,
12111 , 12201 , 12202 , 13001 , 13011 , 20001 , 20002 , 20011 ,
20012 , 20021 , 20022 , 20101 , 20102 , 20111 , 20112 , 20121 ,
20122 , 20201 , 20211 , 20221 , 21001 , 21002 , 21011 , 21021 ,
21101 , 21102 , 21111 , 21201 , 22001 , 22002 , 22011 , 22101 ,
22102 , 22111 , 30001 , 30011 , 30101 , 30111 , 31001 , 31011 ,
31101 , 31111
up to 100000.
Then from 100000 to 500000:
100001, 100002, 100003, 100011, 100012, 100013, 100021, 100022,
100031, 100101, 100102, 100103, 100111, 100112, 100113, 100121,
100122, 100201, 100202, 100211, 100212, 100221, 100301, 100311,
101001, 101002, 101003, 101011, 101012, 101013, 101021, 101022,
101031, 101101, 101102, 101103, 101111, 101112, 101113, 101121,
101122, 101201, 101202, 101211, 101212, 101301, 102001, 102002,
102011, 102012, 102021, 102022, 102101, 102102, 102111, 102121,
103001, 103101, 110001, 110002, 110003, 110011, 110012, 110013,
110021, 110022, 110031, 110101, 110102, 110103, 110111, 110112,
110113, 110121, 110122, 110201, 110202, 110211, 110212, 110221,
111001, 111002, 111003, 111011, 111012, 111013, 111021, 111022,
111031, 111101, 111102, 111103, 111111, 111112, 111121, 111201,
111202, 111211, 112001, 112002, 112011, 112012, 112101, 112102,
112111, 113001, 120001, 120002, 120011, 120012, 120101, 120102,
120111, 120112, 120201, 121001, 121002, 121011, 121101, 121102,
121111, 121201, 122001, 122002, 122011, 130001, 130011, 130101,
130111, 200001, 200002, 200011, 200012, 200021, 200022, 200101,
200102, 200111, 200112, 200121, 200122, 200201, 200202, 200211,
200212, 200221, 201001, 201002, 201011, 201012, 201021, 201022,
201101, 201111, 201121, 201201, 201211, 202001, 202002, 202011,
202012, 202101, 202111, 210001, 210002, 210011, 210021, 210101,
210102, 210111, 210201, 210202, 210211, 211001, 211002, 211011,
211021, 211101, 211111, 212001, 212002, 212011, 212101, 220001,
220002, 220011, 220101, 220102, 220111, 220201, 221001, 221002,
221011, 221101, 300001, 300011, 300101, 300111, 301001, 301011,
301101, 301111, 310001, 310011, 310101, 310111, 311001, 311011,
311101
The gaps, and similarities, surprised me.
January 11, 2011 at 8:30 pm
Let xR denote the digit-reversal of x, and let xS denote the square of x. Then xRS = xSR if and only if xRSR = xS.
All of the steps in multiplying two numbers have left-right symmetry, except for carrying. Thus, we see that RSR is the same operation as S, except that we carry to the right instead of the left.
So if we can square x without any carries, then squaring commutes with digit reversal for that number. It is plausible that the converse is also true, but I do not have a proof.
January 11, 2011 at 11:14 pm
Very nice idea.
But how about 1, 2 & 3 what do we do with them?
Leave a Reply
January 11, 2011 at 2:46 pm
Cool!