Republic of Mathematics blog

Ore numbers: how do they grow?

Posted by: Gary Ernest Davis on: November 15, 2010

Tweet
Share
Pin
Share
0 Shares

Øystein Ore

An Ore number (also known as a harmonic divisor number) is a number whose harmonic mean of its divisors is an integer.

The harmonic mean of a set of numbers \{x_1,\ldots x_k\} is \frac{n}{\frac{1}{x_1}+\ldots +\frac{1}{x_k}}.

When the x_1, \ldots , x_k are the whole number divisors of the number n, then we get the harmonic mean of the divisors of n.

These numbers were named for Øystein Ore who proved that all perfect numbers are Ore numbers. Recall a whole number is perfect if the sum of the divisors of the number is exactly twice the number. 6 and 28 are well-known perfect numbers.

For example, the divisors of 3 are 1 and 3, so the harmonic mean of these divisors is \frac{2}{\frac{1}{1}+\frac{1}{3}}=\frac{3}{2} which is not an integer, so 3 is not an Ore number.

More generally, if p > 1 is a prime number then the harmonic mean of its divisors is \frac{2}{1+\frac{1}{p}}=\frac{2p}{p+1} which is not an integer, so no prime number is an Ore number.

On the other hand, the divisors of 6 are 1, 2, 3 and 6 so the harmonic mean of these divisors is \frac{4}{1+\frac{1}{2}+\frac{1}{3}+\frac{1}{6}}=\frac{24}{6+3+2+1}=2 so 6 is an Ore number.

Using a computational language such as Maple, Mathematica, MATLAB or Python one can calculate a few Ore numbers.

Here is a list of the Ore numbers up to 10,000,000:

1, 6, 28, 140, 270, 496, 672, 1638, 2970, 6200, 8128, 8190, 18600, 18620, 27846, 30240, 32760, 55860, 105664, 117800, 167400, 173600, 237510, 242060, 332640, 360360, 539400, 695520, 726180, 753480, 950976, 1089270, 1421280, 1539720, 2178540, 2229500, 2290260, 2457000, 2845800, 4358600, 4713984, 4754880.

How fast do these Ore numbers grow?

Let’s write O(n) for the n^{th} Ore number.

So, O(1) = 1, O(2) = 6, O(3) = 28, O(4) = 140 and so on.

What does a plot of O(n) versus n look like?

A regression indicates that O(n) grows as a power of n, at least in the range 1 < n < 10000000

A plot of \log (O(n)) \textrm{ versus } \log (n) should therefore look like a straight line, and it does:

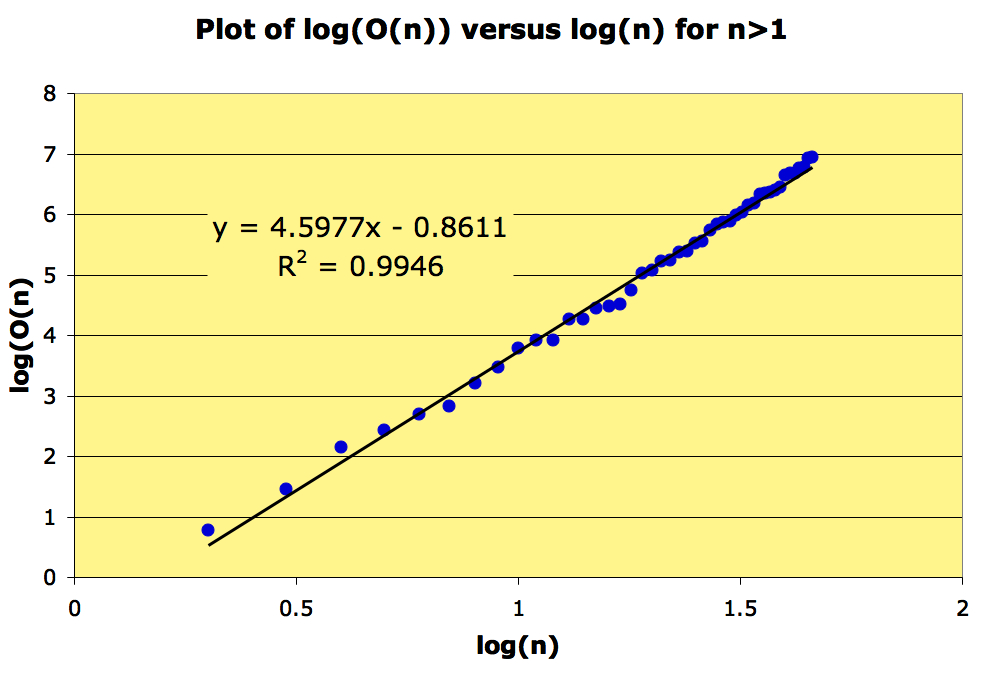This suggest that there are constant A, B such that as n increases, O(n) \approx An^B.

If this is so, then \frac{O(n+1)}{O(n)} \approx \frac{A\times (n+1)^B}{A\times n^B}=(1+\frac{1}{n})^B \to 1 \textrm{ as } n \to \infty.

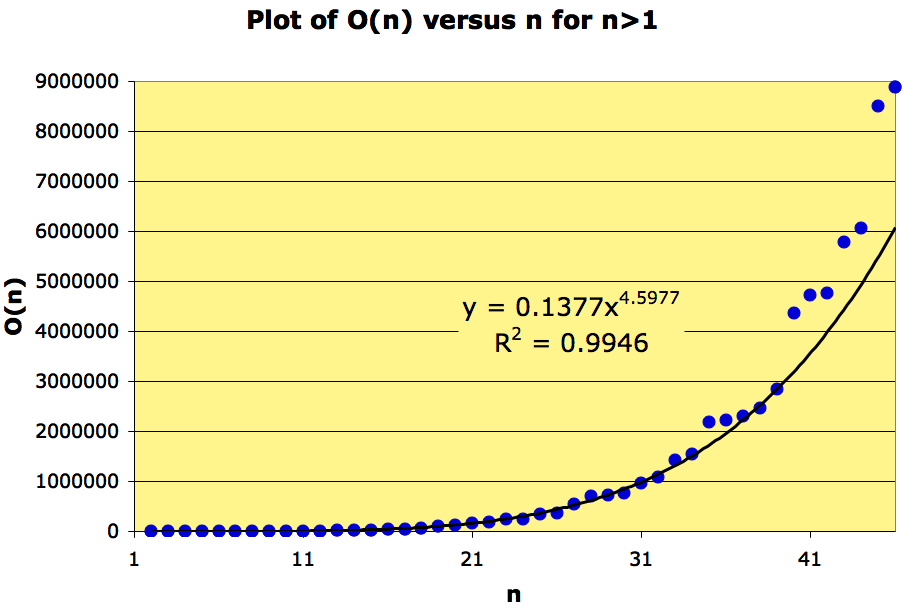
From the data we have for the Ore numbers less than 10000000 the plot of \frac{O(n+1)}{O(n)} \textrm{ versus } n looks as follows:

So,  does \frac{O(n+1)}{O(n)} \to 1 \textrm{ as } n \to \infty ?

This is a weaker question than: “is O(n) \approx An^B for some constants A, B“.

Postscript

  • Here are the Ore numbers up to 1 billion ( = 1,000 million):

1, 6, 28, 140, 270, 496, 672, 1638, 2970, 6200, 8128, 8190, 18600, 18620, 27846, 30240, 32760, 55860, 105664, 117800, 167400, 173600, 237510, 242060, 332640, 360360, 539400, 695520, 726180, 753480, 950976, 1089270, 1421280, 1539720, 2178540, 2229500, 2290260, 2457000, 2845800, 4358600, 4713984, 4754880, 5772200, 6051500, 8506400, 8872200, 11981970, 14303520, 15495480, 16166592, 17428320, 18154500, 23088800, 23569920, 23963940, 27027000, 29410290, 32997888, 33550336, 37035180, 44660070, 45532800, 46683000, 50401728, 52141320, 56511000, 69266400, 71253000, 75038600, 80832960, 81695250, 90409410, 108421632, 110583200, 115048440, 115462620, 137891520, 142990848, 144963000, 163390500, 164989440, 191711520, 221557248, 233103780, 255428096, 287425800, 300154400, 301953024, 318177800, 318729600, 326781000, 400851360, 407386980, 423184320, 428972544, 447828480, 459818240, 481572000, 499974930, 500860800, 513513000, 526480500, 540277920, 559903400, 623397600, 644271264, 675347400, 714954240, 758951424, 766284288, 819131040, 825120800, 886402440, 900463200, 995248800

Leave a Reply

Visitor map

Locations of visitors to this page

Get a free blog at WordPress.com

Theme: Albeo by Design Disease.