Is commutativity of multiplication a natural concept?
Posted by: Gary Ernest Davis on: January 30, 2010
This post is a response to a tweet of Chiara Maieron, and a follow-up from Christopher Simpson.
The original tweet was:
“chiamai @republicofmath Heard kid who could multiply 4*9 but had troubles w 9*4 and wondered if commutativity concept is natural for math students ”
My initial response was that it depends on the kid’s concept of multiplication.
From a mature mathematical perspective, multiplication is essentially repeated addition  and can be defined inductively via and
. Even this abstract mathematical definition requires us to demonstrate that we always have
.
However, Â for school children we do not define multiplication in this way. Â Most commonly, is introduced as m lots of n.
This is how many teachers would like student to think of multiplication, and it is then a nontrivial issue for a child, to appreciate that  m lots of n gives us the same quantity as n lots of m.
Geometrically, with some added color, it is clear this is so:
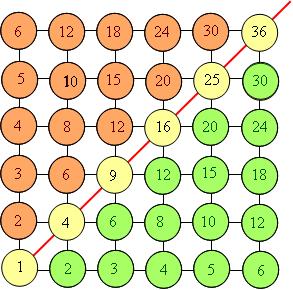
 When, for example, 4 lots of 9 is laid out with lots of 9 as rows, a transposition turns the rows into columns, so 4 columns of 9 rows becomes 9 rows of 4 columns. Â Whichever way we count the total we get 36.
When, for example, 4 lots of 9 is laid out with lots of 9 as rows, a transposition turns the rows into columns, so 4 columns of 9 rows becomes 9 rows of 4 columns. Â Whichever way we count the total we get 36.
But to a young child this might not be obvious until it is either experienced or pointed out.
A mature mathematician might “explain” the commutativity of multiplication by appeal to the inductive definition, and a teacher or child by appeal to transposition of a diagram, as above. Whatever, some level of justification or explanation is in order.
There is, it seems to me, nothing in the concept of multiplication that relieves us of the necessity to explain why it is a commutative operation.
I have found that pre-service elementary teachers benefit from seeing multiplication filled in on the spots of (part of) an integer lattice:
For some reason, that is not quite clear to me, many pre-service elementary teachers find the symmetry of this diagram about the diagonal, shown, to be quite revealing. It is as if the geometric picture encapsulated in one fell swoop their vague, perhaps previously unspoken, understanding that multiplication is commutative.
Let Christopher Simpson and Chiara Maieron have the final words:
“TopherSimpson @republicofmath They always seem to get commutative and associative confused (no matter what I tell or show them). Maybe this will help”
“chiamai @republicofmath Thanks. I was curious because I grew up with the idea that commut. is “natural”, but then as a physicist I learned it is not.”
How not to report Pearson's r: a cautionary tale in mathematical cognition
Posted by: Gary Ernest Davis on: January 27, 2010
Mark Ashcraft is a Professor of Psychology at the University of Nevada, Las Vegas. He specializes in mathematical cognition. In his own words, he:
investigates issues in mathematical cognition, asking questions such as “What do people know about numbers, arithmetic, and math?” and “How do we learn math?”
In 2007 Mark Ashcraft published a paper  in the Psychonomic Bulletin & Review with Jeremy Krause. You can download it here: ASHCRAFT_KRAUSE_2007
The issues discussed in this paper are the connections between working memory, mathematics anxiety, and mathematics performance.
Two main aspects to the argument in the paper, as I understand it, are as follows:
- Many other studies have shown a decrease in mathematics performance in arithmetic problems as working memory is stressed. This seems not only to be true but to be fairly common-sensical: arithmetic problems that have more steps and do not rely on automatic recall make greater demands on working memory. This is associated with longer times to complete problems and an increase in errors.
- Mathematical performance and mathematics anxiety are correlated. They write:
“The higher one’s math anxiety, the lower one’s math learning, mastery, and motivation;”
“highly math-anxious individuals get poorer grades in the math classes they take …”
and:
“These correlations mean, simply but importantly, that as math anxiety increases, math achievement declines.”
On what do they base these latter assertions? They state there is:
- a math anxiety correlation of -0.30 with high school grades,
- a math anxiety correlation of -0.75 with enjoyment of math,
- a math anxiety correlation of -0.64 with motivation to take more math or do well in math;
- a math anxiety correlation of -0.31 with the extent of high school math taken.
They also state that:
“The overall correlation between math anxiety and individuals’ math achievement, as measured by standardized tests, is -0.31.”
Correlations are typically expressed as “r” values. This correlation coefficient r can vary from -1 to 1, with the extremes of -1 and 1 indicating 100% correlation.
So what does a correlation of  -0.30 mean? What interpretation can we give to this? One commonly accepted interpretation is that tells us the degree of variation in the dependent variable (math performance) accounted for by variation in the independent variable (math anxiety).
If what is
? A quick calculation tells us that in this case
which is 9%.
Well, this pretty good, no? 9% of the variation in mathematics performance can be accounted for by variation in math anxiety.
But think of this the other way around: over 90% of the variation in mathematics performance is NOT accounted for by variation in math anxiety. In other words, math anxiety, as an independent variable, does not have much to do with variation in mathematics performance.
How about the highest correlation ? Â In this case
so over 56% of the negatively correlated variation in enjoyment of mathematics is accounted for by variation in math anxiety. This does not seem surprising to me: I expect people who have math anxiety to not enjoy mathematics.
The other low r values all indicate one thing, and that is contrary to Ashcraft and Krause’s conclusion: math anxiety, as an independent variable, does not have much to do with variation in mathematics performance.
The authors go on to draw some speculative educational implications based on these unsound interpretations of low r values.
A danger, dear reader, is that this work may well make its way into educational psychology books and be taught to prospective mathematics teachers as proven fact.
Be wary dear reader. Be numerate and literate, read carefully, and critically. Â It’s a jungle out there!