A rush of connections and insights, a glorious moment of clarity
Posted by: Gary Ernest Davis on: January 19, 2010
Sandra was a pre-service elementary teacher at Rutgers in New Jersey. She came to mathematics methods classes with relatively low expectations:
“When I enrolled in this class back in September, I thought I was signing up for a three-month crash course in the mechanics of mathematics -something which had always eluded me. At that time I could not imagine math as anything more than the relentless stream of equations I used to agonize over as a young student.”
As the weeks went by Sandra’s written reflections reveal that she soon came to class with a specific intention of gaining enlightenment. She was not a student who simply attended class in order to have her presence recorded. She came with specific intentions, one of which was an expectation of moments of insight:
“Last week’s class was wonderful. For the first time since we began, I experienced the succession of ‘ah ha!’ moments I had been waiting for so eagerly.”
As instructor, I was unhappy that students were not expressing clear and unambiguous connections between the combinatorial problems that I had given to them to work on.
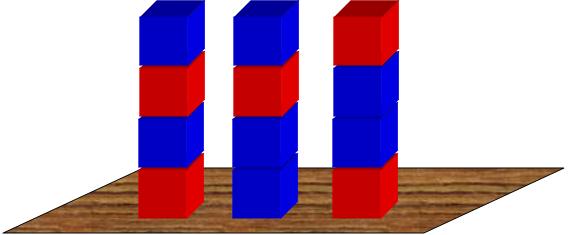
One problem was to figure the number of different block towers  of a given height that can be built from a large supply of red and blue blocks:
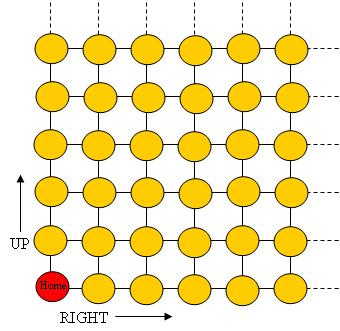
I took another of the combinatorial problems and added an element of chance to it. Students were to toss a coin 4 times in a row.  Starting from the HOME spot on the grid, below, they would, at each toss of the coin, move one step UP on the grid  if the coin came up heads, and RIGHT if the coin came up tails:
The question I set the students was: how will the number of times you land on a given dot pan out as you toss the 4 coins many times?
My aim was to stimulate students to build explicit connections between moves on the grid, and block towers.
Initially Sanda had not seen a connection between the two problems that satisfied her:
“We had been encouraged to think of the two colors in the towers as similar to the ‘Up’ vs. ‘Right’ options in the dot matrix, but this was difficult for me. In the ‘Towers’ activity, we used powers of two and increased them based on the number of blocks in the towers. But with the matrix (= grid), we plotted the number of options to each dot …I did not see powers of two in any of the numbers I was writing in the dots.”
However, with the coin-tossing procedure she suddenly saw something much different:
” As we did the activity, tossing a quarter four times each, I saw that there were only a limited number of answers for each toss based on the constraints of the problem…only 2 sides to the quarter and only four tosses. And I quickly saw that those dots were beginning to arrange themselves along a diagonal. And what did all those dots along that diagonal have in common? They were the only solution you could have when tossing a quarter exactly four times. And if you added up the number of options along that diagonal, you got a number which was 2, 4, 8, 16, 32 & 64 respectively. Powers of two. Suddenly I saw why the ‘Towers Problem’ could be solved using powers of two … and I saw how increasing the blocks in the towers moved the answers to the next diagonal and thereby to the next power of two. And I saw how the number of options increased systematically as each square’s options compounded with the addition of more variables.”
Sandra understood – she saw – that the rows of Pascal’s triangle – the diaognals of the grid -Â add to powers of two. However, Sandra’s deepening perception and understanding of connections did not stop there. With the sudden understanding for how the powers of two entered the picture she made another fundamental realization about the proportions of marks on the grid spots 4 steps from “home”:
“Now I could see fractions expressed in our grid, because each dot represented a specific fraction of chances that it could be expressed given the intervals.”
This realization was both emotional and liberating. In one short episode of about 20 minutes Sandra woke from her mathematical slumbers:
“And I knew then, that different approaches worked for different people, and that’s why we need to acknowledge all the different ways we solve a problem. For some people building towers worked, for some it was the grid matrix and for others it was (a+b). it was tremendous to feel something abstract becoming concrete…to finally see algebra as a way of making sense of the world around you. I saw the connection between the 4 toss quarter game and the dot grid. I saw the way the number of tosses translated into a diagonal line across the grid. And I saw how certain dots were ‘hit’ more than others due to the number ways (sic) to reach that dot. And what was most momentous to me was seeing that the number of dots or ‘hits’ along that diagonal added up to a number that equaled the power of two associated with the number of ‘intervals’ or ‘jumps’.”
That moment of seeing a connection – of the mind and brain constructing a new vision of the perceptual material already in front of the student – is powerfully emotional:
“SO what have I learned? Well, that sometimes, it takes a number of different approaches or methods to help students understand math. It didn’t become clear to me until we did the coin toss. And there was a rush of connections and insights.”
Toward the end of a fifteen week semester – some 9 weeks after she had a sudden insight into connections between towers, grid walks and binomial expansions, and coin tossing – Sandra worked in a group on determining empirically the distribution of black and white sides showing when 6 Othello pieces (black on one side, white on the other) were tossed randomly from a bag.
Sandra, unlike others in her group, detached from the empirical activity and began drawing a grid, labeling the spots on the grid with the number of different ways of reaching that spot by walking UP or RIGHT (the entries in Pascal’s triangle). She worked at this until she completed the 6th diagonal.
When the class results for the empirical activity were pooled the result was 3 whites and 3 blacks occurring most often – 29 % of the time.
Noting Sandra’s approach, I asked her what she had obtained. She replied with an answer of 20 divided by , which another student calculated as 0.31.
This was a stunning example of flexible thinking, using long-term knowledge in a new context. Yet Sandra was critical of her memory in a reflection written after this episode. She apologized, following the class, for not being able to remember the entries in the  6th row of Pascal’s triangle, and described her memory as “poor”.
Sandra’s “rush of connections and insights” were emotionally laden cognitive insights that etched themselves deep in her memory. They impressed themselves so powerfully in her memory that she was able, during the remainder of the semester to bring these memories back to mind and to use them in differing settings, some not directly related to the context in which the memories were formed. However Sandra’s recollections of those memories was, in her view, “poor”. She still equated good mathematical memory with rote recollection of complicated formulas or facts, in precise detail, rather than a recollection of a broad cognitive road-map, based on an emotional episode.
Sandra also wrote in her weekly reflections:
“I look forward to those rare, but beautiful opportunities to make connections across the discipline, knowing that it is those eureka moments which make it all worth while. And I can’t wait until the day when I have the privilege of seeing my students experiencing those same moments of clarity and comprehension, exhilaration and accomplishment.”
Working with other colleagues, particularly Mercedes McGowen, formerly at William Rainey Harper College in Chicago, Â we find that teaching this way – focussing on connections between different mathematical problems – we cannot “teach” students to see connections.
We can set up conditions under which their sudden enlightenment is more likely, but ultimately it is not a matter of learned behavior, rather of the students’ direct noticing and seeing. These moments of vision on the part of students are usually accompanied by expressions of intense pleasure and wonder.
It is those moments we seek to capture and to highlight, to refer our students back to “when you saw …”. This gives our students the possibility of a new way of understanding mathematics, and a new way of remembering.
Those who have clear visions of connections, and who forge strong episodic memories no longer see mathematics as a collection of unrelated facts and formulas. Things make sense for them, and it is exactly the memory of the sense-making that constitutes what mathematics is for them now.
The advantages of this are enormous – instead of mathematics being laborious and hard to remember, it is now easy and pleasurable. So we now teach to foster such memories: strong, vivid, episodic memories of seeing connections between different parts of mathematics.
She bet me $5 she wouldn't learn any mathematics
Posted by: Gary Ernest Davis on: January 18, 2010
Some years ago I taught mathematical methods to prospective elementary teachers at Washington State University in Pullman, Washington. In a class of 30 or so students there might be 2 or 3 young men, the rest being young women, principally from the Seattle area.
Many of these prospective elementary teachers would volunteer they were math phobic. When someone mentioned math phobia, I would ask people in the class to raise their hand if they were math phobic, and to only leave it raised if that meant shaking at the thought of algebra or possibly wanting to vomit if they had to do fraction problems. Usually 10-15 hands out of 30 were raised and stayed raised. Many of these students had very bad experiences in mathematics, and were afraid and sickened at the thought of having to teach mathematics to young children.
Apart from teaching these prospective teachers about mathematics, how to teach mathematics, and how to become mathematics teachers, I also had to inject a large dose of therapy in the form of making mathematical experiences light, enjoyable, fun, empowering and enlightening.
One semester, in 2003 as I recall, a young women, Jennifer, told me about the second week that although she liked me, and liked my class, she was not going to learn anything about mathematics or about teaching it from me. She was, she told me, such a hopeless case that I would not be able to impart any such knowledge to her.
Now I love a challenge! So I asked Jennifer if  she would agree to a bet: I would bet her I could, contrary to her expectations, not only teach her relevant mathematics but enable her to teach it to others.  She, of course, bet I could do no such thing. We agreed to put up $5 each, winner take all, on this bet. We each gave $5 to one of the other students to keep for us, and the class went on as usual.
As a mathematician teaching mathematical methods to prospective teachers I had been a bit leary of getting students to practice arithmetic in different bases: a common practice among teacher educators. My initial thoughts were that this is a time-wasting exercise. As I thought about it, however, I came to the conclusion that working in a different base forced prospective teachers into the position of naive learners, and stimulated them to think about the deeper aspects of our base 10 system.
One morning, after mid-semester, I came to class with a bunch of cartoon cutouts. Students were to work in groups. One group would be the octopus group and they would do arithmetic in base 8. Another group was the Mickey Mouse group and they also would do arithmetic in base 8. The ostrich group would have to do arithmetic in base 4.  Jennifer’s group was the pirate group, and with the cartoon pirate having only one hand – the other being a hook – the pirate group would have to do arithmetic base 5.
My condition for doing arithmetic – addition, subtraction, multiplication and division of whole numbers – was that translation back into the familiar base 10 was not allowed.
I explained what I wanted by using a language analogy. It was as if they were transported to a Filipino community where everyone spoke Tagalog, and no-one spoke English. They, the students, would have to rapidly learn to speak and think in Tagalog, without translating in their heads into English.
Of course they found this difficult, especially when, doing addition, they had to carry digits. The different bases were forcing them to think what the digits meant in a place value system.
Jennifer’s group were having a particularly hard time of it. There were three other young women in this group and addition and subtraction in base 5 was proving hard for them. As I watched, Jennifer explained to one of the others how the carrying went. Jennifer seemed to have cottoned onto the idea. As she explained her understanding to the others in the group there were frowns and looks of puzzlement. Jennifer was a little frustrated and repeated her own understanding, telling the others how easy it was.
At that point I stopped the class and announced that people were making good progress, but that there were still some points that needed clarification, particularly with regard to carrying. I feigned looking around the class for someone who might explain this and lighted upon Jennifer.
“Jennifer, you seemed to know how to do this. Could you explain it to the rest of the class? ”
She looked a little surprised, but went to the board and wrote her explanation and talked it through as she wrote. Other students asked questions and she answered  them patiently and with clarity. Several times she stated how obvious this was.
As Jennifer looked around for other questions she saw me at the back of the room, smiling.
“Oh no!” she said. “I’ve just lost my bet!”
I couldn’t have been happier to take her money.
This story sticks in my mind for several reasons, not the least of which is the sense of achievement Jennifer felt in class that day. She now knew, with certainty, what it felt like to learn and teach mathematics. It wasn’t always hard, it wasn’t mysterious:Â it just took attention and thought. Â And it could actually be quite easy.
I have also thought often, of how relatively rare are those moments in class, and what I can do to stimulate them. I’ve had other similar experiences, but not enough that I could say with any assurance, that I knew how to remedy prospective teachers mathematical phobias in one semester.
I do know that creating an atmosphere in which these experiences might take place is a necessary condition to resolving student fears. Â I also know that some students need a lot longer than a semester for this to happen.
I hope, but do not know, that these young prospective teachers will find a caring mentor when they are in schools teaching.
I hope, but do not know, that they will be able to reach back into some positive experiences they had and say that’s how they would like their classes to be.
I hope, but do not know, that they will pass on an attitude of digging deeper and deeper into mathematics, in such a way as to encourage  light, enjoyable, fun, empowering, and enlightening experiences.