A little bit of pi(e)
Posted by: Gary Ernest Davis on: January 15, 2010
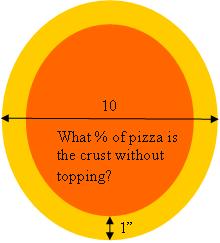
My wife likes to eat at Not Your Average Joe’s on Route 6 in Dartmouth, Massachusetss. I’m a vegetarian so my choices are more lmited. NYAJ has passable choices for a vegetarian, inlcuding pizzas. Usually a 10″ garden pizza does me.
When I first started ordering pizzas from Joe’s I was still teaching pre-service elementary teachers mathematics, so when I noticed that Joe’s leaves a full 1″ of pizza crust without any sauce or topping I thought: what a good exercise to get my students to figure out the percentage of pizza without topping.
In my experience most people don’t think to quantify their experiences this way. I think they should – it can be an eye-opener. If you doubt me, think about the price of toner-cartridge ink in dollars per gallon. Â This is what quantitative literacy is about.
Here’s a picture of pizzas from Joe’s on-line menu:

and here’s a diagram of what I was looking for:
Not all pre-service elementary teachers recall how to calculate the area of a circular region, but in a class of 25 or so usually someone does.
So, someone in the class calculates that the area of the whole pizza is  square inches.
At this point some students want to repace  by
to get an area of approximately 78.6 square inches.
Surprisingly, to me, some students do not approximate . It seems almost as if they can see that the occurrences of
will cancel as they calculate the percentage of the pizza without topping.
They next calculate that the area of pizza with topping  is square inches, so the area of pizza without topping is
square inches.
The ratio of the area of pizza without topping to the area of the pizza is .
So 36% of the pizza has no topping. Wow! That’s over of the entire pizza! Shouldn’t Joe’s lower their  prices?
This result is almost always an eye-opener to pre-service elementary teachers. They find it hard to believe that so much of the area of the pizza lies around the edge.
Usually I ask them to calculate the percentage of pizza without topping if they don’t know the diameter, but know that 1″ of the crust has no topping. This level of algebraic thinking usually stumps them.
When the class is happy with their answer I ask them how they know that the area of a circular region with diameter is
, or, in other words, that the area of a circular region of radius Â
is
.
Invariably it’s just a formula they remember, if they did in fact remember it. Those who didn’t remember it usually agree that it sounds right.
When I ask them what is , I either get an answer of
or something like: “It’s the circumference; it’s like, the circumference is
times the radius.”
So what some of them seem to know about is that  a circle of radius
has a circumference of
.
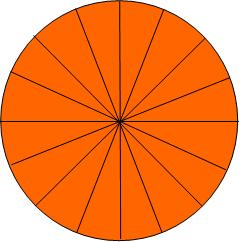
Building on that, I draw a pizza of radius with many more slices than usual:
I then take those slices and arrange them side by side, alternately one up, one down:
With very thin slices the rearranged pizza is looking very much like a rectangle, with width approximately half the circumference  of the circle, and height approximately the radius of the circle:
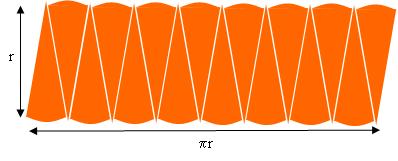 So with very thin slices the area of the rearranged pizza is approximately
So with very thin slices the area of the rearranged pizza is approximately .
This is an approximation, but as the pizza slices are made thinner and thinner it is a better and better approximation.
_______________________________________________
The strange fact of a large proportion of the area of a circular region lying close to the perimeter is related to the annoying phenomenon of looking for a place in a road map and finding it near the edge of the page, so having to go to the next page for a complete picture.
Of course this recollection is getting pretty old-fashioned as GPS replaces paper maps. But for those of us who recall it, here’s what happens:
Let’s suppose the maps are drawn on US letter, , and that we are annoyed if the place we want is within
” of the edge of the page. How often are we likely to be annoyed?
The area of the page is 93.5 square inches, and the area of the region within ” of the margin is
square inches.
Supposing the place we want is more or less randomly distributed on the page we will be annoyed  % of the time – about 1 time in 5.
Reducing cognitive load in algebra
Posted by: Gary Ernest Davis on: January 13, 2010
 Many years ago I used to get very annoyed with John Sweller, an Australian academic who aggressively pushed his idea of cognitive load as a panacea for problem solving in mathematics. John upset a lot of people in the Australian mathematics education community because they felt he was talking about routine problems, and not what they saw as problem solving.
Many years ago I used to get very annoyed with John Sweller, an Australian academic who aggressively pushed his idea of cognitive load as a panacea for problem solving in mathematics. John upset a lot of people in the Australian mathematics education community because they felt he was talking about routine problems, and not what they saw as problem solving.
I have since come to understand better that John’s theory of cognitive load has to do with working memory, the very real constraints on it, and the means that he described and analyzed to reduce the load on working memory in cognitively difficult situations.
So today I am to sing the praises of John  Sweller and his cognitive load theory.
What stimulated me to do this  is the following recent Tweet:
@Educator Just uploaded 60+ free examples of Algebra 1 onto YouTube! http://ow.ly/Vt9k #TUalg1
I went to the site and looked at a few of the algebra videos advertised.
Folks, I have to say this: I was not happy.
The “follow-me, do as I do” style of presentation of algebra is something I do not like.
I thought about this as I drove my wife to the train at 6:30 this morning, and agonized over whether I should write this post. Â After all, who wants to be negative about colleagues who are trying hard to educate kids?
The folks at Educator.com seem to have their hearts in the right place, and they are doing a great job getting this site up and running. More power to them. Â On Twitter, @Educator describes Educator.com as a: “Pioneering E-Learning Startup aimed to equalize education. Specializing in Algebra, Biology, Calculus, Chemistry, Java, Physics, Statistics, Trigonometry.”
I had decided to shelve writing about this until I could put my money where my mouth is and show how to do better. After all, criticism is easy; getting out there and do something creative and productive is hard, and that’s what Educator.com is doing. I admire them for that.
But I looked at the video on the distributive property in algebra, thought of John Sweller and cognitive load, and … here we are.
The video that got me thinking about cognitive load is this one:
The video set up has a women explaining a procedure for expanding a polynomial expression (the screen states this is “simplifying” the expression. In my considered mathematical view the final result is less simple than the expression at the beginning).
The task is to simplify (by which they mean “expand”):
Looking at this – already simplified – expression, and thinking about cognitive load, what I notice right away is that pesky sitting outside the parentheses.
I know, as an experienced mathematician and educator, that  the combination of the “-” sign, the number “3” and the term is likely to cause a problem for many students. The “-” sign and the
term are particularly apt, even on their own, to cause difficulties, and together they are much more likely to do so.
For a kid who is just learning this – and therefore watching this explanatory video – Â there’s a lot to bring to mind and to keep in working memory.
How might we reduce the cognitive load of this expansion?
First off, Â what have we got here? We have two polynomials and
that we have to multiply out, using the distributive property. Â Right away we notice that the first polynomial is a monomial – it is just a number times
.
Let’s focus on just the part first, so reducing the number of things of which we have to keep track. Â The index laws – so nicely explained in the video – tell us that multiplying a polynomial in
by
will simply raise the powers of
by 2.
If we do not do this simpler step  first we run the risk of overloading our working memory with the “-” sign and the number 3.  This is what Sweller urges us to avoid. And sure enough the person talking in the video forgets to write the term in the first multiplication! Dang cognitive load went and got her!
A less cognitively demanding first pass at this expansion would be something like:
Having got that far we can forget all about the term and focus on the “-3” term. Working memory is feeling relieved!
But we know how often we can get those pesky negative number multiplications wrong, so let’s just distribute the “3” over the new polynomial first:
OK! that was easy enough. Now to deal with the pesky “-” sign. Well, multiplying by changes all positive coefficients to negatives and negatives to positives, so:
So, I sing the praises of John Sweller. He was right. I misunderstood him, and I think mathematics educators need to pay real close attention to reducing cognitive load in mathematics problems.
Educator.com is doing a good job. I congratulate them. They could be doing a great job, positively impacting millions of young students.