The distributive property
Posted by: Gary Ernest Davis on: January 10, 2010
This post is about the following fact: for whole numbers
.
Sometimes this is called the distributive property of multiplication over addition, and sometimes it is called the distributive law. Some people are uncomfortable with use of the word “law”, as if it were passed by fiat and we darned well better follow it or else. Â That’s not what the word “law” means in mathematics, but to avoid those sort of associations, let’s just call it the distributive property.
In the set of natural numbers the distributive property can be proven true from the standard Peano axioms.
However, school mathematics does not deal with natural numbers. That comes later, in college, when students learn about foundational issues in mathematics, such as what are sets, axioms for sets, axioms of infinity, and so on. Â In school we deal with the counting numbers .
What we know about the counting numbers has to come from acts of counting, not by inductive proof. So the distributive property in school mathematics needs to be placed in the context of counting, since we are dealing, in school , with counting numbers, a much less formal notion than natural numbers.
A simple version of the distributive property is for all counting numbers
.
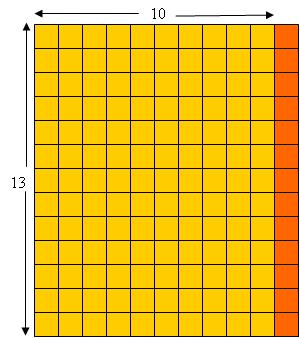
This simple version of the distributive property has a very nice, simple interpretation in terms of units of the number “a”. To illustrate this through a concrete example, let’s look at :
Here, as adults, we can see the column of 13 small squares as a unit that is repeated 11 times. The very simple form of the distributive property says that we can split off 1 of those units, and count 10 lots of the unit 13, and then add in the extra unit of 13. Sort of obvious when you see it this way.
However, many children, even in grades 3-6, are not entirely stable or comfortable counting in units. Often young children, 6 years old, will recite count by 2’s: , … If they are able to do this they will happily show you that they can do so.
However, they may not yet be able to count by units of 2. For example, if a child can recite by 2’s, tell them you were counting by 2’s to 24 and ask them how many times you counted. Some children, not all, will answer 12, usually tapping two fingers as they count, or perhaps nodding their head as they recite 2’s. These children are counting their acts of reciting by 2’s, and are able to count by units of 2. The ability to do this develops gradually, and by grades 3-6 most, but not all, children will be confident counting by units. If they are not, the distributive property is going to cause them some difficulty.
Additionally, young children, in grades 1- 3, often cannot see rectangular arrays the way adults see them: as repeated rows, or repeated columns, where the rows, or columns, are themselves built from repeated squares.
Seminal studies by Lynne Outhred and her doctoral adviser Michael Mitchelmore show convincingly the developmental steps involved in young children’s ability to recognize and reproduce rectangular arrays as repeated rows of repeated squares. Here is an example from a paper of theirs [Student’s_structuring_of_rectangular_arrays] which illustrates some of the development steps children go though in being able to communicate in a drawing what constitutes an array:
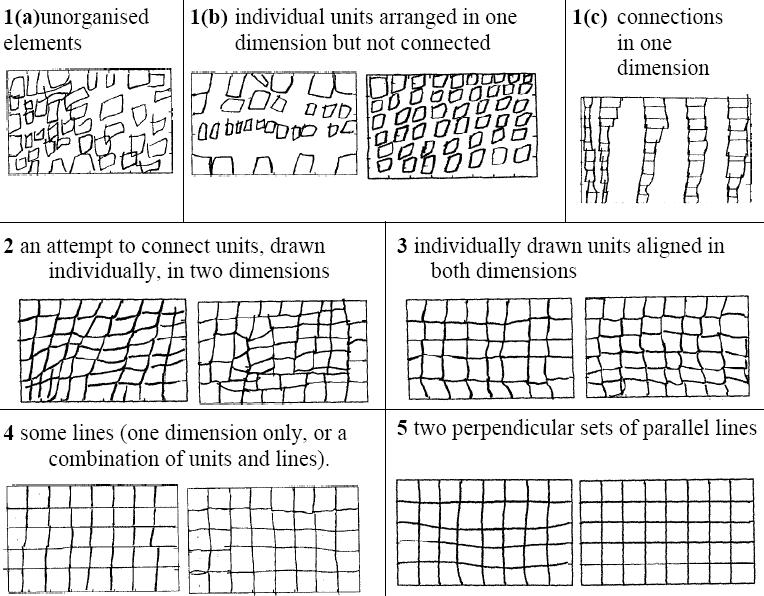
So this simple form of the distributive property, so clearly illustrated for an adult by a rectangular array, may not be so clear to a child who (a) is not yet confidently counting by units or (b) is still developing the skill of seeing a rectangular array as composed of rows and columns.
As adults we take these two developmental skills for granted, because it’s hard to imagine a time when we did not have them. But clearly, at age 1 month we did not, and somewhere before age 21 years we probably did. These skills did not just pop into our heads fully formed, so we went through a period of developmental in gaining these skills. So, do all children. Â It is advantageous for us, as parents and teachers, to figure out where children are before we begin “explaining” the distributive property to them.
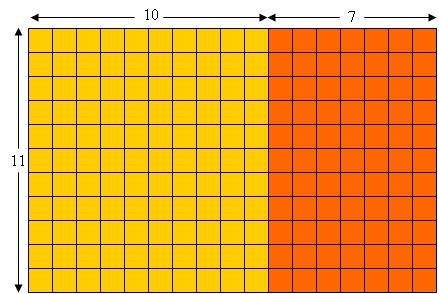
The more general distributive property  also has a simple interpretation in terms of rectangular arrays – simple for an adult that is.  Here is an array decomposition illustrating
:
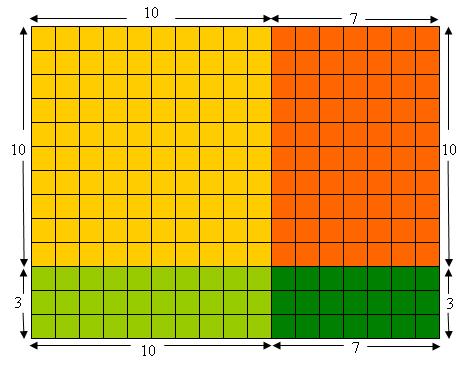
Repeating the distributive property allows us to see that for all counting numbers we have
.
Again this can illustrated nicely by a decomposition of a rectangular array. For example, here’s an array decomposition illustrating :
But we have to bear in mind, As I wrote above, that just because these are  simple and compelling explanations of the distributive property for us, as adults, it does not follow that a child will have the necessary skills to see what we see so clearly.
The distributive property is very important for algebra. One reason is because of its applications, for example in multiplying binomial expressions . Another reason is that a grasp of the distributive property is a good indication of a student’s number sense and that, in turn, is an excellent indicator of how readily a student can grasp algebraic ideas.
Mathematics is not (only) a language
Posted by: Gary Ernest Davis on: January 9, 2010
Every so often someone will assert that mathematics is a language.
What  concerns me about the statement “mathematics is a a language”  is what I am not hearing directly: “mathematics is ONLY a language”  which I worry is implicit.
For example in an interview, Paul Samuelson, Â said:
 Well, my belief is that nothing that can be expressed by mathematics cannot be expressed by careful use of literary words. All the mathematics itself originally grew out of axioms — assumptions stated in words — and [it reminds me of] the only speech that the great Willard Gibbs, at Yale, ever gave at a faculty meeting, when there was a debate between studying languages and mathematics. He said four words: “mathematics IS a language.” And that’s on the frontispiece of my Foundations of Economic Analysis, but I’ve written somewhere that he should have cut it down to three words: “Mathematics is language.” It’s just a very compact form of language.
Well, my belief is that nothing that can be expressed by mathematics cannot be expressed by careful use of literary words. All the mathematics itself originally grew out of axioms — assumptions stated in words — and [it reminds me of] the only speech that the great Willard Gibbs, at Yale, ever gave at a faculty meeting, when there was a debate between studying languages and mathematics. He said four words: “mathematics IS a language.” And that’s on the frontispiece of my Foundations of Economic Analysis, but I’ve written somewhere that he should have cut it down to three words: “Mathematics is language.” It’s just a very compact form of language.
So there we have it from the winner of the 1970Â Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel himself: Mathematics is just a very compact from of language.
This view of mathematics – that it is just a language for expressing something about another topic of interest, such as physics, economics, chemistry, sociology – Â is common among users of applied mathematics For such people mathematics is not their major concern. Rightly so – their focus of attention is on physics, or chemistry, or economics. If they could avoid mathematics altogether they probably would.
But what about people who are mathematicians: are they really just a bunch of linguists, getting together to discuss the language of mathematics? Wouldn’t you think that the people whose life is mathematics might know if mathematics is just a language?
My own view is that mathematics is a science – it is  a science of number, space, pattern and arrangement.
If this view has any validity then mathematics ought to have well established facts. Does it? You bet it does, and one of the great grand-daddy facts of mathematics is the prime number theorem.
The prime number theorem is not “just language”. It is a deep fact about the way prime numbers are spaced out in the collection of whole numbers. It was discovered empirically by Gauss and Legendre, and proved to be true by Jacques  Hadamard.
The prime number theorem asserts that the prime number is approximately equal to
, with the relative error of this approximation approaching 0 as
 increases without bound.  Here
is the natural logarithm of
: Â the area under the curve
from
.
Alain Connes has asserted that we know such facts about mathematical reality better than we know any fact about physical reality. He writes:
“The scientific life of mathematicians can be pictured as a trip inside the geography of the mathematical reality which they unveil gradually in their own private mental frame.” [A_view_of_mathematics]
Connes has even gone so far as to assert:
Is this an isolated example, essentially the only real fact in mathematics. No, to the contrary, mathematics is full of mathematical facts.
 Here’s another simple, but beautiful fact discovered by Euler and overlooked by the ancient Greeks in their study of polyhedra. A polyhedron has a number of vertices (v), edges (e) and faces (f). Euler discovered, and proved, that v-e+f=2.  Is this just a language statement. No: it is a provable, but non-obvious, fact about plane graphs which applies to the graphs of  polyhedra.
Here’s another simple, but beautiful fact discovered by Euler and overlooked by the ancient Greeks in their study of polyhedra. A polyhedron has a number of vertices (v), edges (e) and faces (f). Euler discovered, and proved, that v-e+f=2.  Is this just a language statement. No: it is a provable, but non-obvious, fact about plane graphs which applies to the graphs of  polyhedra.
Dave Richerson has a beautiful account of this lovely finding of Euler in his book Euler’s Gem. If you still think that mathematics is (only) a language, do yourself, and me, a favor by getting hold of this book and reading it with pleasure. It is a beautifully written book, that tells what the science of topology is about.
So mathematics is a subject with deep facts, and is not just a language for expressing facts about some other topic.
Where, then does the idea that mathematics is just a language come from? I have already said that users of mathematics in other fields often see mathematics this way. But where did they learn that? My view is that school mathematics by and large promotes this idea that mathematics is just a language, because school mathematics is, by and large, devoid of mathematical facts. School mathematics is, in the main, a collection of recipes and methods for doing … who knows what.
It’s time, in my view, for an infusion of facts and mathematical science into school mathematics. Â Then we might get kids loving mathematics, as we might if we read Dave Richerson’s lovely book.