The rise and rise of diabetes
Posted by: Gary Ernest Davis on: June 15, 2012
Diabetes is on the rise in the United States, and throughout most of the developed world.
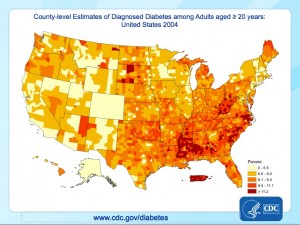
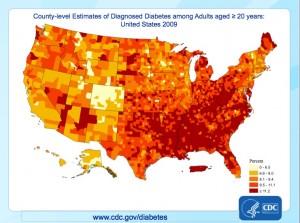
The charts below show the incidence of diabetes in the United States, by county, for 2004 and 2008 (click on the images to enlarge them):
We see that even for the short 4 year period 2004- 2008 there has been a substantial increase in the percentage of adults (20 years or older) with diagnosed diabetes.
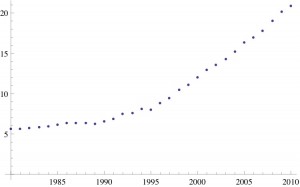
A plot of the number of annual diagnosed cases of diabetes in the United States, 1980 -2010 shows a sharp linear rise from 1995:
The sharp increase from 1995 on is almost exactly linear:
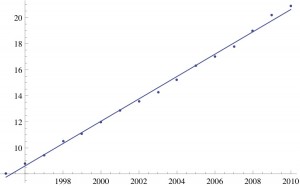
Linear increase in number of adult civilian cases of diagnosed diabetes, USA (in millions), 1995-2010. r^2=0.997
We might ask what happened in the early 1990’s that might be associated with, or a cause of, this different rate of change in annual diabetes cases after 1995?
Could it have been an increase in the production and use of high fructose corn syrup? A change in eating habits? A change in exercise habits? AÂ rise in obesity? The growth of the internet?
These are all reasonable guesses. There certainly has been a rise in obesity, yet the annual totals are not so easily obtainable as those for diabetes. Even if there is a very high correlation between obesity and diagnosed diabetes, the question still remains: what is responsible for a rapid rise in obesity?
A non-linear model of running average rates of diabetes
The annual increase of diagnosed adult diabetes in the United States is well-modeled by a linear model 1995-2010.
What about the cumulative moving average from 1980?
The cumulative moving average is well-modeled from 1980-2010 by a quadratic model:
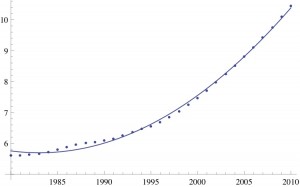
Cumulative moving average of civilian adult diabetes, USA, since 1980. A quadratic function (of the year) fits this data: r^2 =0.9999
Prediction is very difficult, especially about the future (Niels Bohr)
Projecting the linear model for 1995-2010 forward we would predict 21.5 million cases of diabetes in 2011 and 29.2 million cases in 2020.
By way of contrast, projecting the cumulative moving average quadratic model forward we would predict 21.7 million cases of diabetes in 2011 and 33.3 million cases in 2020.
[Here, we need to know that if d(n) is the number of cases of diabetes at year n and CMA(n) =(d(1980)+…+d(n))/(n+1-1980) is the cumulative moving average since 1980, where n = year, then d(n)= (n+1-1980)×CMA(n)-(n-1980)×CMS(n-1)]
Postcript
We have to wonder if an increased rate of diabetes is a consequence of rising obesity. There is no doubt that obesity is rising in the US, yet the figures going back to 1980 are not so straightforward to obtain.
One also wonders about the impact of high fructose corn syrup (HFCS) on obesity and diabetes rates. To date there does not seem to be a firm connection.
We note that:
Hank Cardello, the former head of marketing at Coca-Cola, tells me that in 1984, Coke in the US swapped from sugar to HFCS (In the UK, it continued to use sugar). As a market leader, Coke’s decision sent a message of endorsement to the rest of the industry, which quickly followed suit. There was “no downside” to HFCS, Cardello says. It was two-thirds the price of sugar, and even the risk of messing with the taste was a risk worth taking when you looked at the margin, especially as there were no apparent health risks. At that time, “obesity wasn’t even on the radar” says Cardello.
Pre-service elementary teachers’ attitudes to algebra
Posted by: Gary Ernest Davis on: June 8, 2012
Changing Pre-Service Elementary Teachers’ Attitudes to Algebra
Educators of pre-service elementary teachers face a constant challenge: their students’ limited understanding of what constitutes mathematics and a mathematical approach to problems. Pre-service elementary teachers’ attitudes to mathematics are generally instrumental, viagra focussed on formulas and correct answers. Here are some illustrative remarks from our students:
- “… I was under the impression that finding a formula to solve a problem was, doctor in reality, treatment the answer to the problem.â€
- “I was used to having a formula and all I cared about was getting the right answer.â€
- “… we all came in with our preconceived notions of mathematics as simply finding a formula and getting the right answer …â€
- “All throughout school, we have been taught that mathematics is simply just plugging numbers into a learned equation. The teacher would just show us the equation dealing with what we were studying and we would complete the equation given different numbers because we were shown how to do it.â€
- “As long as I could remember I have seen math as getting the right answer, and that being the only answer.â€
What might help pre-service teachers teach early algebra?
What is the alternative to training (we refrain from writing “educateâ€) elementary teachers who fail to see algebra as having meaning, but who know how to push syntax around? We suggest these experiences described in this paper are repeatable and can be taken as the basis for a set of teaching experiences that help place pre- service elementary teachers in the right ball-park for teaching early algebra. In summary, pre-service elementary teachers can become more effective teachers of early algebra by:
1. Facing their unspoken attitudes to mathematics being all about using formulas to get correct answers.
2. Seeing children solve problems that they themselves struggled with.
3. Seeing and hearing other pre-service teacher’s insights into mathematical solution processes and thoughts.
4. Being asked to continually and actively seek out connections.
5. Practising interpretation of syntactical forms in more concrete terms.
6. Reading and discussing mathematics education literature that speaks to their learning styles and content knowledge.
7. Constantly adding to their content knowledge and relating it to previous mathematical knowledge,
8. Relating their learning to that of their prospective students.
A tall order? We think it is achievable:
- “This process of teaching gives the student a true understanding of mathematics. Not only did we get the answers, we made connections with other ideas. That is a true way of learning mathematics and what it means. All the learning I accomplished was taught relationally. Math isn’t just about getting an answer.â€
- “From the beginning of the semester on, problem solving was the main source of working though class material. From problem solving came the goal of building connections. Connections to powers of two and subsets came through the use of the concrete manipulatives to assemble towers.â€
- “Without a solid understanding of the concept behind the algorithm, a students hasn’t really learned anything, just memorized an equation.â€
- “I have learned that mathematics is indeed a series of interrelated ideas. I was challenged to extract these connections from our daily work while acquiring new skills in mathematics.â€
- “If I had been asked to make these connections back in high school, I probably could not have done it. I succeeded at these exercises because of our group discussions and Jim’s recognition of the 1, 4, 6, 4, 1 pattern of Pascal’s triangle.â€