Republic of Mathematics blog

Growth rates of simple integer recurrences

Posted by: Gary Ernest Davis on: June 5, 2012

In: Uncategorized
1 Comment

The sequence of integers $A(n)$ defined by $A(1)=2 \textrm{ and } A(n)= \lfloor(3/2)A(n-1)\rfloor$ – where $\lfloor x\rfloor$ , the floor of $x$ , is the greatest integer $\leq x$ – beginsÂ 2, 3, 4, 6, 9, 13, 19, 28, 42, 63, 94, 141, 211, 316, 474, 711, 1066, 1599, 2398, 3597, 5395, 8092, 12138, 18207, 27310, 40965, 61447, 92170, 138255, 207382, 311073 and grows rapidly.

One can numerically estimate the growth rate of this sequence by first observing that the sequence of positive numbers $\frac{A(n)}{(3/2)^n}$ is decreasing. This follows from the inequality $A(n) =\lfloor(3/2)A(n-1)\rfloor \leq (3/2)A(n-1)$ upon dividing by $(3/2)^n$ , to get $\frac{A(n)}{(3/2)^n}\leq \frac{A(n-1)}{(3/2)^{n-1}}$ .

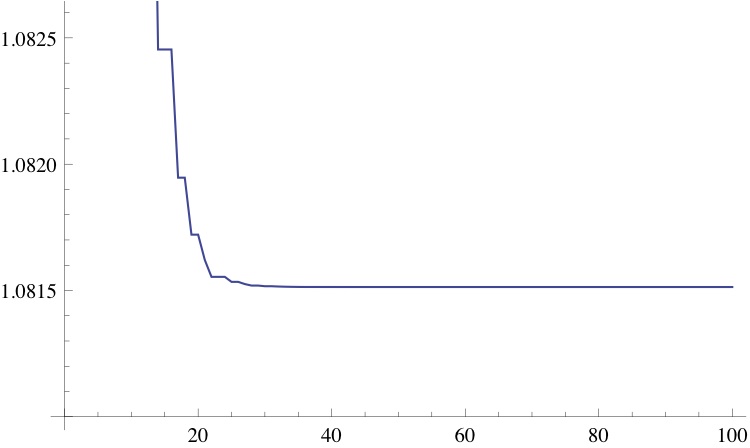
This means the sequenceÂ $\frac{A(n)}{(3/2)^n}$ has a limit. In fact this sequence converges fairly rapidly to the limit:

n	A(n)/(3/2)ⁿ	n	A(n)/(3/2)ⁿ
1	1.33333333333	34	1.08151439525
2	1.33333333333	35	1.08151405187
3	1.18518518519	36	1.08151382295
4	1.18518518519	37	1.08151382295
5	1.18518518519	38	1.08151382295
6	1.14128943759	39	1.08151375512
7	1.11202560585	40	1.08151375512
8	1.09251638470	41	1.08151372497
9	1.09251638470	42	1.08151370487
10	1.09251638470	43	1.08151369148
11	1.08673587473	44	1.08151368254
12	1.08673587473	45	1.08151367659
13	1.08416675918	46	1.08151367262
14	1.08245401549	47	1.08151366997
15	1.08245401549	48	1.08151366997
16	1.08245401549	49	1.08151366880
17	1.08194653587	50	1.08151366880
18	1.08194653587	51	1.08151366880
19	1.08172098938	52	1.08151366880
20	1.08172098938	53	1.08151366880
21	1.08162074649	54	1.08151366880
22	1.08155391790	55	1.08151366869
23	1.08155391790	56	1.08151366862
24	1.08155391790	57	1.08151366862
25	1.08153411684	58	1.08151366862
26	1.08153411684	59	1.08151366860
27	1.08152531636	60	1.08151366860
28	1.08151944938	61	1.08151366859
29	1.08151944938	62	1.08151366859
30	1.08151684183	63	1.08151366859
31	1.08151684183	64	1.08151366859
32	1.08151568292	65	1.08151366859
33	1.08151491032	66	1.08151366859

So we see that $A(n)\approx 1.08151366859(3/2)^n$ for large $n$ .

What if we replace the constant 3/2 by a parameter $r$ ?

How does the sequenceÂ $A(n)$ defined by $A(1)=2 \textrm{ and } A(n)= \lfloor rA(n-1)\rfloor$ grow?

As before we see there is a constant $K(r)$ such that $A(n)/r^n \to K(r) \textrm{ as } r \to \infty$

An obvious question is: how does $K(r) \textrm{ vary with } r$ ?

A moment’s thought shows that the answer is only interesting for $r \geq 3/2$

The following MathematicaÂ® code computes $K(r)$ to a decent approximation:

A[1, r_] = 2;
A[n_, r_] := A[n, r] = Floor[r*A[n – 1, r]];
T = Table[{r, Table[N[A[n, r]/r^n], {n, 1, 100}][[-1]]}, {r, 1.5, 5, 0.001}];
ListPlot[T, Joined -> True]

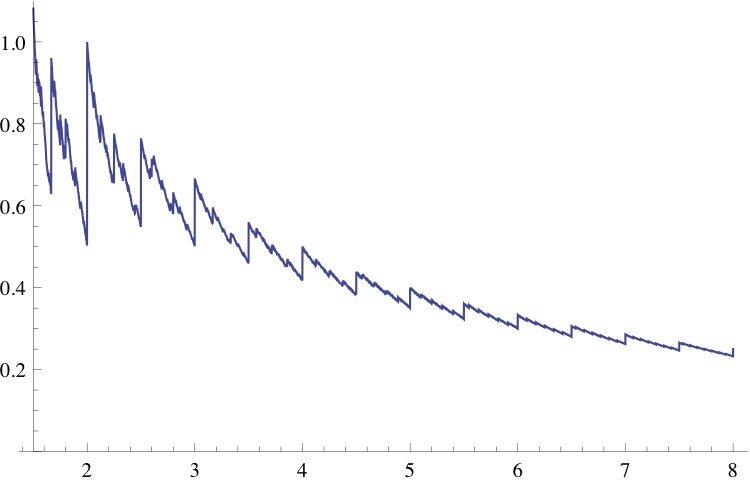
and the resulting plot of $K(r) \textrm{ versus } r$ looks as follows:

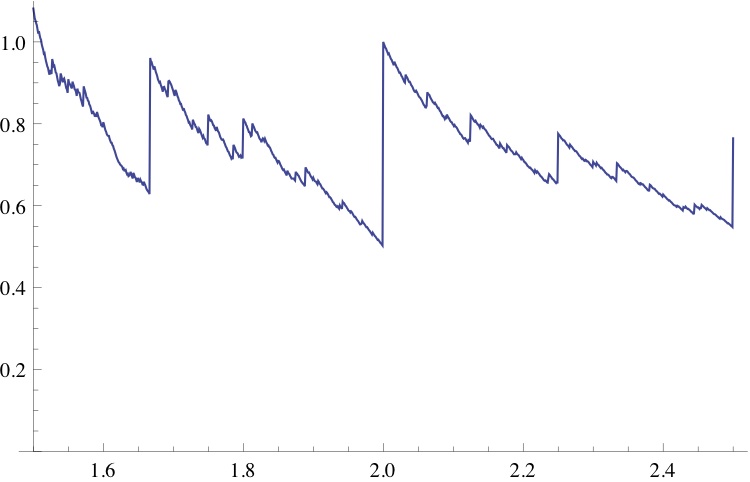
A blow-up of the portion of the plot for $1.5 \leq r \leq 2.5$ looks as follows:

Mississippi, West Virginia and Alabama biggest losers in obesity stakes – Colorado clear winner

Posted by: Gary Ernest Davis on: June 5, 2012

In: Uncategorized
Leave a Comment

The Centers for Disease Control and Prevention website has a very interesting series of graphics depicting adult obesity rates in the United States by State and by year from 1985 through 2010.

Obesity for this purpose is defined as a body mass index (BMI) of 30 or above.

The changes year by year are dramatic.

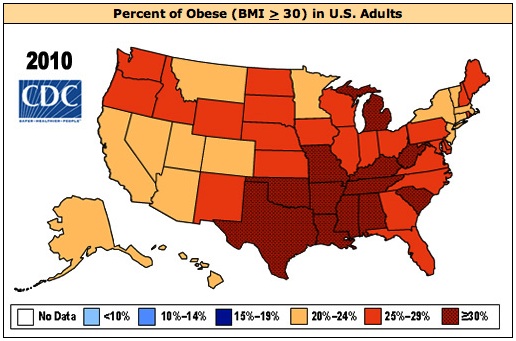
The percentages of adults in the various states that are obese by this definition are shown for 2010 in the graphic below:

The States, buy sorted by percentage of obese adults from largest to smallest, patient is shown in the table below, together i the z-scores for those percentages (for this purpose the District of Columbia is counted as a State)

STATE	% PEOPLE WITH BMI >30	Z-SCORE
Mississippi	34	2.17
West Virginia	32.5	1.70
Alabama	32.2	1.61
South Carolina	31.5	1.40
Kentucky	31.3	1.33
Texas	31	1.24
Louisiana	31	1.24
Michigan	30.9	1.21
Tennessee	30.8	1.18
Missouri	30.5	1.09
Oklahoma	30.4	1.05
Arkansas	30.1	0.96
Indiana	29.6	0.81
Georgia	29.6	0.81
Kansas	29.4	0.75
Ohio	29.2	0.68
Pennsylvania	28.6	0.50
Iowa	28.4	0.44
Illinois	28.2	0.37
Delaware	28	0.31
North Carolina	27.8	0.25
South Dakota	27.3	0.10
North Dakota	27.2	0.06
Maryland	27.1	0.03
Nebraska	26.9	-0.03
Maine	26.8	-0.06
Oregon	26.8	-0.06
Florida	26.6	-0.12
Idaho	26.5	-0.15
Wisconsin	26.3	-0.21
Virginia	26	-0.31
Rhode Island	25.5	-0.46
Washington	25.5	-0.46
New Mexico	25.1	-0.58
Wyoming	25.1	-0.58
New Hampshire	25	-0.62
Minnesota	24.8	-0.68
Alaska	24.5	-0.77
Arizona	24.3	-0.83
California	24	-0.92
New York	23.9	-0.96
New Jersey	23.8	-0.99
Vermont	23.2	-1.17
Montana	23	-1.23
Massachusetts	23	-1.23
Hawaii	22.7	-1.33
Utah	22.5	-1.39
Connecticut	22.5	-1.39
Nevada	22.4	-1.42
District of Columbia	22.2	-1.48
Colorado	21	-1.85

The States with a z-score greater than 1 areÂ Mississippi, West Virginia, Alabama, South Carolina, Kentucky, Texas, Louisiana, Michigan, Tennessee, Missouri and Oklahoma.

The States with a z-score less than -1 areÂ Vermont, Montana, Massachusetts, Hawaii, Utah, Connecticut, Nevada,District of Columbia and Colorado.

Mississippi is at the extreme with a z-score above 2, and Colorado lies at the other extreme with a z-score of almost -2

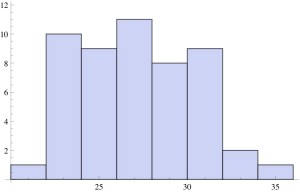
These outliers can be visualized from the histogram of the percentages of obese adults:

This histogram is fairly flat, indicating a relatively uniform distribution with the exception of Colorado, with only 21% of obese adults, at the low end, Â and Alabama, West Virginia and Mississippi with more than 32% of obese adults, at the high end.

Southern cooking might be tasty, but it seems there might be something about the mountain air of Colorado that is associated with a lower obesity rate.

On the other hand, if we multiply the percentage rates of obese adults by the population, for each state, we get the number of obese adults per state:

STATE	OBESE POPULATION/ 2010	Z-SCORE
Â California	8940949	4.04
Â Texas	7795124	3.41
Â Florida	5001148	1.86
Â New York	4631366	1.65
Â Pennsylvania	3632880	1.10
Â Illinois	3618238	1.09
Â Ohio	3368659	0.95
Â Michigan	3054045	0.78
Â Georgia	2867545	0.68
Â North Carolina	2650864	0.56
Â New Jersey	2092471	0.25
Â Virginia	2080266	0.24
Â Tennessee	1954600	0.17
Â Indiana	1919205	0.15
Â Missouri	1826623	0.10
Â Washington	1714758	0.04
Â Maryland	1564633	-0.05
Â Arizona	1553260	-0.05
Â Alabama	1539075	-0.06
Â Massachusetts	1505955	-0.08
Â Wisconsin	1495677	-0.08
Â South Carolina	1456990	-0.10
Â Louisiana	1405345	-0.13
Â Kentucky	1358222	-0.16
Â Minnesota	1315373	-0.18
Â Oklahoma	1140411	-0.28
Â Colorado	1056131	-0.33
Â Oregon	1026728	-0.34
Â Mississippi	1008881	-0.35
Â Arkansas	877691	-0.43
Â Iowa	865165	-0.43
Â Kansas	838817	-0.45
Â Connecticut	804172	-0.47
Â Utah	621874	-0.57
Â Nevada	604923	-0.58
Â West Virginia	602223	-0.58
Â New Mexico	516854	-0.63
Â Nebraska	491286	-0.64
Â Idaho	415409	-0.68
Â Maine	356001	-0.71
Â New Hampshire	329118	-0.73
Â Hawaii	308788	-0.74
Â Rhode Island	268405	-0.76
Â Delaware	251422	-0.77
Â Montana	227565	-0.79
Â South Dakota	222271	-0.79
Â North Dakota	182945	-0.81
Â Alaska	174007	-0.82
Â Vermont	145172	-0.83
Â Wyoming	141470	-0.83
Â Washington, DC	133583	-0.84

We see that California and Texas account for a significant number of the total of obese adults in the US.

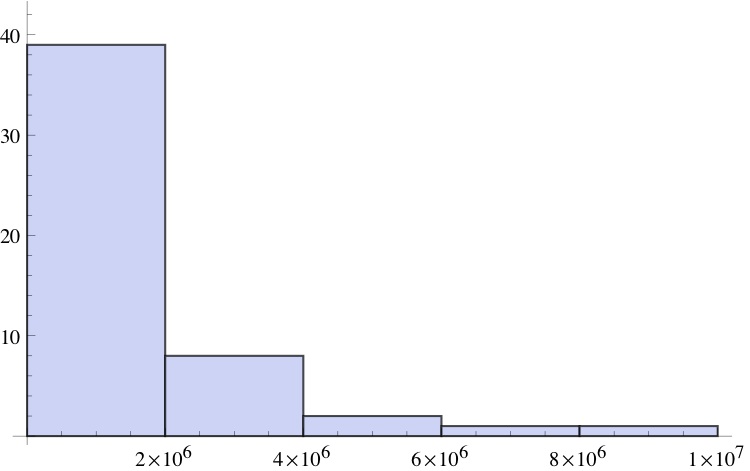
A histogram of the population data for obesity shows how skewed is the distribution of state numbers of obese adults (as distinct from percentages)Â :

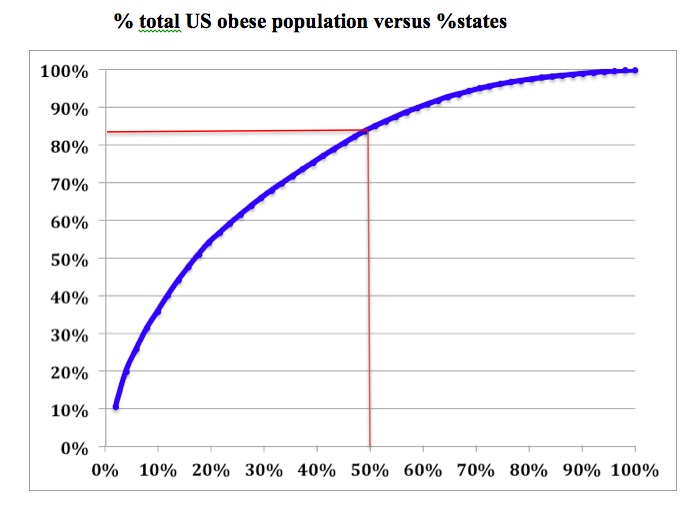
In fact, if we plot the cumulative percentage of obese adults in the states, versus the cumulative percentage (out of 51) of the states (including DC) we get the following curve, which shows, for example, that the half the states account for approximately 85% of all US obese adults:

Tags: obesity

Republic of Mathematics blog

Growth rates of simple integer recurrences

Mississippi, West Virginia and Alabama biggest losers in obesity stakes – Colorado clear winner

Math Blogging

Great mathematics sites

Visitor map