Republic of Mathematics blog

Who’s kidding who? What do tests test?

Posted by: Gary Ernest Davis on: June 7, 2011

In: Uncategorized
7 Comments

What does a test “test”?

All over the world, at all levels of education, mathematics teachers set tests for their students, and give grades on the basis of those tests.

Tests are usually thought to be reliable indicators (if not measures) of how well studentsÂ engage with the material being taught to them, and is often believed to be related in some correlational way with their mathematical ability.

Where a student ranks – their class standing – on a test may well be an indicator of both those things.

I want to argue, however, that what a test really tests is the teacher. A test, in my view and experience, tests a teacher’s ability to set a test at the “right” level.

Typically, students will be awarded a percentage score on a test, indicating the fraction of available points a student obtained as a result of the correct answers they gave.

Standards for grading answers vary widely. Some teachers give partial credit, some do not. Some teachers are lenient in relation to answers that require interpretation, others are not.

A certain number of percentage points is taken to be a pass. Below that critical percentage a student is deemed to have “failed”, above it the student has “passed”.

In many cultures, particularly that of North America, a mere “pass” is regarded by students and their parents as a shameful outcome. In my experience the overwhelming majority of North American students see themselves as A or B students, and certainly not as D students.

Grading standards vary widely in the United States.

One variant, not uncommon in my experience is to convert percentages into letter grades as follow:

A = 90% or higher

B = 80%â€“89%

C = 70%â€“79%

D = 60%â€“69%

F = 0%â€“59%

The interpretation of these letter grades varies quite a bit.

For example, college students often may not count a grade below C as a “pass” for the purposes of their major, but may count a “D as a “pass” if it is a subject outside their major. For example, many engineering students can carry a D in calculus as a passing grade.

The typical college level passing percentage in Australia is 50%, and in the United Kingdom it is 40%.

Curiously, academic standards in these countries, overall, seem to be in inverse proportion to the passing percentage. The UK has generally higher academic standards than Australia , which, in turn, has generally higher academic standards than does the Unites States.Â What I mean by “higher academic standards” is that an any given level of academic attainment one will find UK students to be generally more advanced in knowledge skills and achievement than Australian students, who in turn are generally more able than students in the United States, at the same grade level.

How does a teacher construct a test?

A colleague changed the order of the questions on a test for a course he taught each year, and obtained disastrous results. Typically his students would study tests from previous years in preparation for that year’s test. The mere fact of changing the order of questions was enough to send a number of students into a tail spin.

Teachers can easily set a test for which all but the best and brightest students will fail to pass. This does not require setting material that students have never seen: just pushing the standards a little on reasoning and rigor will generally do it. Or just change the order of the questions from previous years’ tests.

Teachers who do this regularly will be seen by their colleagues as being too tough, unrealistic, and out of touch.

On the other hand it is easy to set a test for which all but the least diligent students will pass, and for which most students will do very well: simply focus on routine calculational questions, all of which have been practiced often beforehand.

Teachers who do this will be seen by their colleagues as too easy, too soft, and not fulfilling their obligations to properly assess students.

So a conscientious teacher wants to steer a course between being overly demanding, and being too soft.

Using various skills and prior experience, therefore, a teacher will generally set a test that has a likely outcome of a reasonable number of students passing, not too many top marks, and a few, but not too many failures.

In other words, what is being tested when a teacher constructs a test is, in fact, the teacher’s ability to set an “appropriate”, or satisfactory, test.

The myth of objectivity

Many people, especially administrators, like test scores because they are apparently “objective”.

This imagined objectivity is illusory for several reasons.

We have already addressed how a teacher needs to carefully construct a test so that not everyone fails, not everyone does exceptionally well, and is such that their colleagues are satisfied they are doing an adequate and appropriate job of assessment.

There is no objective standard for this: it is simply a matter of practice embedded in a particular culture.

Even within a given test culture there is the problem, in testing mathematics, of giving partial credit, of deciding what to do if a student makes a simple calculational error but then proceeds more or less correctly in their application and reasoning following that.

A final grade- percentage or letter – is an average of points obtained as a result of many such decisions.

There is very little that is objective about this process.

To see why, one needs only give the same test papers to a colleague, with the same grading instructions, and see how the awarded grades vary. Even more telling is for a teacher to re-grade test papers a week or so later and see how consistent are the grades.

The pain of believing in the objectivity of test scores

Students who fail to pass mathematics tests usually believe they are failures.

They are not.

They may not have studied all the material at a depth that would make a pass or higher grade likely, they may have been ill for some or all a semester, they may have had family problems, they have have seriously misunderstood a teacher’s intentions and instructions. They may have attention deficit disorder, be highly anxious, or be on medications that affect their ability to focus.

Al of these factors are real and should be understood as real mitigating factors.

Believing in the objectivity of a test and the consequent view of oneself as a failure is highly damaging. It lowers self-esteem and inhibits future effort.

Conversely, students who do study conscientiouslyÂ who are relatively free of stress,Â and who score highly on tests are very likely to see their success as an intrinsic ability: they begin to see themselves as “A” students. Such students may well have high or even exceptional ability, but a class test is not providing evidence for that. What the test provides evidence for is that some factor, or combination of factors, lead a student to a good outcome. Those factors can include high ability, but almost certainly will include time spent studying, effective study habits, belonging to a study group of peers, asking questions of the teacher, taking notes, listening carefully, a low stress environment, and a dash of luck. Believing in the objectivity of tests leads a student to attribute their success on tests to only one of the factors: ability.

Should we use tests?

I don’t know.

I don’t any more because I see tests as testing my ability to set them appropriately, and not testing the intrinsic ability of students.

I can get an estimate of student work habits from tests, but frankly I’m not much interested in a test to tell me this when I see them regularly in class working on projects. I can see how much work they are putting in: I do not need a summative test to tell me that.

Franky I feel we put too much emphasis on tests and examinations. My own preference is for more collaborative project work in which students can exercise their ability to think, to reason, to plan, and to work toward a goal, utilizing their skills and talents in conjunction with others.

Education, for me, should be a win-win activity, not something we carry out to determine – by phony means in my view – who is a success and who a failure.

Tags: examinations, mathematics, tests

Spotting patterns and finding explanations: Dijkstra’s fusc function

Posted by: Gary Ernest Davis on: May 18, 2011

In: Uncategorized
5 Comments

Edsger Wybe Dijkstra

Edsger Dijkstra named the integer valued function, fusc, of a non-negative integer variable, as follows:

$\textrm{fusc}(0)=0$ ,

$\textrm{fusc}(1)=1$ ,

$\textrm{fusc}(2n)=\textrm{fusc}(n)$ and

$\textrm{fusc}(2n+1)=\textrm{fusc}(n)+\textrm{fusc}(n+1)$

Dijkstra’s writings on fusc can be found at the Edgar W. Dijkstra Archive (EWD 578).

The values of fusc can be computed in any decent programming language (one that has a built-in routine for recognizing odd and even integers – otherwise one has to define such a routine, or include it in the definition of fusc).

Here is a simple Mathematicaâ„¢ definition that allows us to compute fusc easily:

fusc[0] = 0;
fusc[1] = 1;
fusc[n_] := If[Mod[n, 2] == 0, fusc[n/2], fusc[(n – 1)/2] + fusc[(n + 1)/2]]

Here are the first 100 values of fusc:

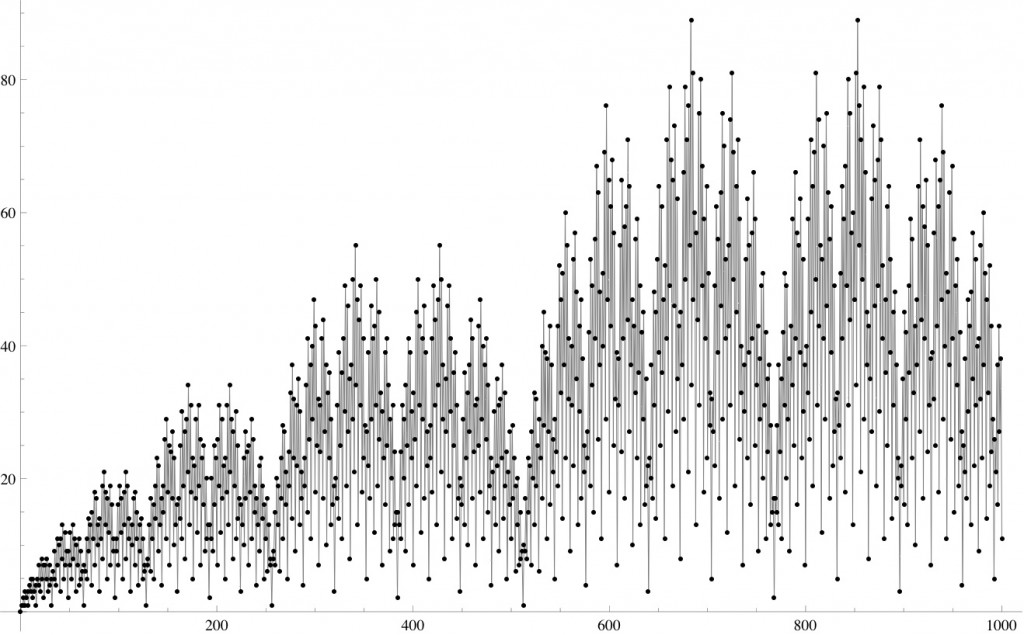
0, 1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4, 1, 5, 4, 7, 3, 8, 5, 7, 2, 7, 5, 8, 3, 7, 4, 5, 1, 6, 5, 9, 4, 11, 7, 10, 3, 11, 8, 13, 5, 12, 7, 9, 2, 9, 7, 12, 5, 13, 8, 11, 3, 10, 7, 11, 4, 9, 5, 6, 1, 7, 6, 11, 5, 14, 9, 13, 4, 15, 11, 18, 7, 17, 10, 13, 3, 14, 11, 19, 8, 21, 13, 18, 5, 17, 12, 19, 7, 16, 9, 11, 2, 11, 9, 16, 7

and a plot of $\textrm{fusc}(n)$ versus $n$ for $0\leq n \leq 1000$ :

Spotting a pattern

Among other properties of fusc, Dijstrka noticed that $\textrm{fusc}(n)$ is a multiple of 2 exactly when $n$ is a multiple of 3.

For example, we see that for multiples of 3 up to 99, the value of fusc is a multiple of 2:

n = multiple of 3	fusc(n)
0	0
3	2
6	2
9	4
12	2
15	4
18	4
21	8
24	2
27	8
30	4
33	6
36	4
39	10
42	8
45	12
48	2
51	12
54	8
57	10
60	4
63	6
66	6
69	14
72	4
75	18
78	10
81	14
84	8
87	18
90	12
93	16
96	2
99	16

Equally, for values of $n$ up toÂ 100 that are not multiples of 3, $\textrm{fusc}(n)$ is not a multiple of 2.

Explaining a pattern

This empirical observation requires explanation.

Mathematics thrives on spotting and explaining patterns, especially unexpected patterns, for which there is no immediate reason why they should hold.

To begin looking for a reason for this empirical observation let’s assume that $n$ is a multiple of 3.

$n$ is either even or odd, so let’s assume first that it is even.

Then $n=6p$ for some non-negative integer $p$ .

This gives us $\textrm{fusc}(n)=\textrm{fusc}(6p)=\textrm{fusc}(6p/2)=\textrm{fusc}(3p)$ .

Now when $p\geq 1, 3p$ is a smaller multiple of 3 than is $6p$ , so if we assume, inductively, that for all smaller multiples of 3 we already know the value of fusc is a multiple of 2, then we know that $\textrm{fusc}(n)$ is also a multiple of 2.

What if $n\geq 1$ is a multiple of 3 and is odd?

Then $=6p+3$ for some non-negative integer $p$ , so $\textrm{fusc}(n)=\textrm{fusc}(\frac{n-1}{2})+\textrm{fusc}(\frac{n+1}{2}) =\textrm{fusc}(3p+1)+\textrm{fusc}(3p+2)$

Now, $3p+1\textrm{ and } 3p+2$ are smaller than $n$ , so we can assume we already know their fusc values, but because these numbers are not multiples of 3, we can assume that we already know their fusc values are not multiples of 2.

In other words, we already know that $\textrm{fusc}(3p+1)$ is odd and $\textrm{fusc}(3p+2)$ is odd, so their sum is even, and therefore $\textrm{fusc}(n)$ is even.

This reasoning tells us:

If $n$ is a multiple of 3 then $\textrm{fusc}(n)$ is a multiple of 2 ………… (*)

What if $n$ is not a multiple of 3?

Can we reason, as the evidence suggests, that $\textrm{func}(n)$ is not a multiple of 2?

If $n \geq 1$ is not a multiple of 3 then $n=3p+1$ or $n=3p+2$ for some non-negative integer $p$ .

We first consider the case $n=3p+1$ .

$n$ is either even or odd, so let’s assume first that it is even.

In this case $p=2k+1$ is odd so $\textrm{fusc}(n)=\textrm{fusc}(n/2)=\textrm{fusc}(3k+2)$ .

Because $3k+2$ is smaller than $n$ and is also not a multiple of 3, we can assume that we already know $\textrm{fusc}(3k+2)$ is not a multiple of 2.

Therefore, in this case, $\textrm{fusc}(n)$ is not a multiple of 2.

Now consider the case where $n$ is odd.

In this case $p=2k$ is even so $\textrm{fusc}(n)=\textrm{fusc}(6k+1)=\textrm{fusc}(3k)+\textrm{fusc}(3k+1)$ .

In this sum we can assume we already know the values of $\textrm{fusc}(3k)$ and $\textrm{fusc}(3k+1)$ and that $\textrm{fusc}(3k)$ is even while $\textrm{fusc}(3k+1)$ is odd.

Therefore $\textrm{fusc}(3k)+\textrm{fusc}(3k+1) =\textrm{fusc}(n)$ is odd.

This deals with the case when $n=3p+1$ . The case $n=3p+2$ is dealt with similarly.

So we have established:

If $n$ is a not a multiple of 3 then $\textrm{fusc}(n)$ is notÂ a multiple of 2 ………… (*)

and combining (*) and (**) we have:

$\textrm{fusc}(n)$ isÂ a multiple of 2 exactly when $n$ is a multiple of 3 ………… (***)

The basis of this reasoning is induction. Because we calculate fusc recursively we can assume, when calculating, $\textrm{fusc}(n)$ that we already know properties of $\textrm{fusc}(m)$ for values $m\leq n$ .

The induction needs a starting point, just as does the calculation of values of fusc, so we need to check these assumed properties are true for $n=0,1$ (which they are).

Explorations

Dijkstra raised the question of when $\textrm{fusc}(n)$ is divisible by 3. Such divisibility questions do not have clear and simple answers, yet lead into deeper and interesting explorations.

The first few integers $n$ for which $\textrm{fusc}(n)=3$ are 5, 7, 10, 14, 20, 28, 40, 56, 80, 112, 160, 224, 320, 448, 640, 896, 1280, 1792, 2560, 3584

Show $\textrm{fusc}(n)=3$ exactly when $n=5\times 2^k \textrm{ or } n=7\times 2^k$ .

Tags: Dijkstra, fusc, induction, proof