Catalan pseudo-primes

Posted by: Gary Ernest Davis on: May 16, 2011

In: Uncategorized
Leave a Comment

Catalan pseudoprimes

As a special case of Fermat’s little theorem, if $p$ is an odd prime number then $2^p-2$ is divisible by $p$ , or, in the language of congruences, $2^p \equiv 2 (mod \phantom{.}p)$ .

The converse of this is not true: if $2^p \equiv 2 (mod \phantom{.}n)$ where $n$ is a positive integer, it does not follow that $n$ is prime. For example $n$ could be $561 = 3\times11\times 17$ . There are infinitely many such $n$ .

Composite integers that pass a test for prime numbers are commonly known as pseudoprimes. Of course whether a composite number is regarded as a pseuodprime depends on the particular prime number property we are using.

Another property of primes involves the Catalan numbers. These are the numbers $C_n$ defined by the recurrence relation $C_0=1$ and $C_{n+1}=C_0C_n+C_1C_{n-1}+\ldots+C_{n-1}C_1+C_nC_0 \textrm{ for } n \geq 0$ .

The Catalan numbers can also be defined recursively by $C_{n+1}=\frac{2(2n+1)}{n+2}C_n \textrm{ for } n\geq 0$ .

The Catalan numbers are the coefficients of $x$ in the series expansion of $\frac{1-\sqrt{1-4 x}}{2 x}=1 + x + 2x^2 + 5x^3 + 14x^4 + 42x^5 + 132x^6 + 429x^7 + 1430x^8 + 4862x^9 + 16796x^10+\ldots$

The Catalan numbers up to $C_{25}$ are

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452.

Clearly $C_n$ grows rapidly with $n$ . In fact $C_n \sim \frac{4^n}{n^{3/2}\sqrt{\pi}}$ in the sense that the ratio of $C_n$ to $\frac{4^n}{n^{3/2}\sqrt{\pi}}$ approaches 1 as $n \to \infty$ :

Theorem 2 of Aebi & Cairns (see below) provides a property of prime numbers in terms of Catalan numbers:

If $p$ is an odd prime, then $(-1)^{\frac{p-1}{2}} .C_{\frac{p-1}{ 2} }\equiv 2 (mod \phantom{.}p)$

On the other hand, there are numbers other than primes that also have this property, for example $p=5907 = 3\times11\times179$ .

Aebi & Cairns call a composite number $n$ a Catalan pseudoprime if $(-1)^{\frac{n-1}{2}} .C_{\frac{n-1}{ 2} }\equiv 2 (mod \phantom{.}n)$ . Thus, 5907 is a Catalan pseudoprime.

Currently the only known Catalan pseudoprimes are:

$5907=3 \times 11\times179$
$1093^2 = 1093 \times 1093$
$3511^2 = 3511 \times 351$

The following two lines of MathematicaÂ® code:

n = 1;
While[Or[Mod[(-1)^((n – 1)/2)*CatalanNumber[(n – 1)/2], n] != 2, PrimeQ[n] == True], n = n + 2]

found 5907 in 1.86 seconds.

Beyond that things are much more difficult.

A related question

The Catalan numbers are related to the middle binomial coefficients $\left(\begin{array}{c c} n-1 \\ \ (n-1)/2 \end{array}\right)$ . When $n$ is odd, say $n =2k+1$ , we have $\left(\begin{array}{c c} n-1 \\ \ (n-1)/2 \end{array}\right) = \left(\begin{array}{c c} 2k \\ \ k \end{array}\right)$ . A theorem of ErdÃ¶s (see Finch, 2007, below) shows that almost always the middle binomial coefficient $\left(\begin{array}{c c} 2k \\ \ k \end{array}\right)$ is divisible by high powers of small primes. Let $g(k)$ denote the smallest odd prime dividing $\left(\begin{array}{c c} 2k \\ \ k \end{array}\right)$ . How does $g(k)$ vary with k? A plot of $g(k) \textrm{ versus } k \textrm{ for } 2\leq k\leq 10000$ is shown below.

This plot indicates that although $g(k) =3$ commonly, there are values of k for which $g(k)$ becomes much larger. In light of the theorem of ErdÃ¶s cited above, a fundamental question is whether the numbers $g(k)$ stay bounded as k increases.

The plot below shows the running average of the values of $g(k)$ . It indicates that, possibly, $lim_{k\to\infty}\frac{1}{k}(g(2)+\ldots+g(k))=3$ .

Behavior of a number-theoretic function

The function $c(k) :=(-1)^k \left(\begin{array}{c c} 2k \\ \ k \end{array}\right)\phantom{.}(mod \phantom{.} 2k+1)$ takes the value 1 exactly when $2k+1$ is prime or a Catalan pseudoprime. How does $c(k)$ behave as a function of $k$ ?

A plot of $c(k) \textrm{ for } 1 \leq k \leq 5000$ , below, indicates that $c(k)$ is bounded above by a linear function of $k$ but has wide variation:

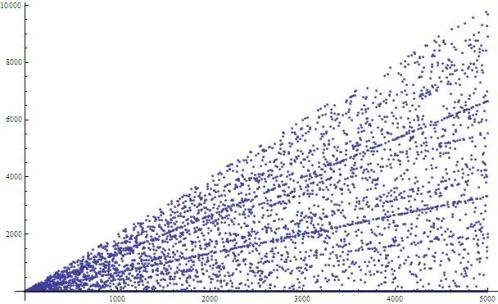
A plot for $1\leq k \leq 20000$ shows similar behavior, but appears more dense on the same scale:

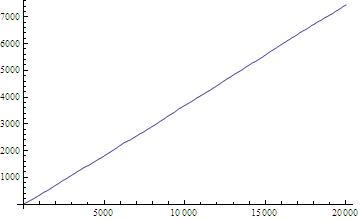
This is more or less what we would expect if the values of $c(k)$ distributed themselves relatively uniformly across the remainders $mod \phantom{.} 2k+1$ . A plot of the running average $\mu(k):=\frac{1}{k}\sum_{i=1}^k c(i)$ , and of the running standard deviation $\sigma(k):=\sqrt{\frac{1}{k}\sum_{i=1}^k(c(i)-\mu(k))^2}$ , indicates a linear increase with $k$ :

Running average of c(k)

How does the function $ac(k) :=(\left(\begin{array}{c c} 2k \\ \ k \end{array}\right) - (-1)^k )/(2k+1) \phantom{.}(mod \phantom{.} 1)$ behave as a function of $2k+1$ ? The plot below indicates that the values are not uniformly distributed:

A blow-up around the value $\frac{1}{3}$ shows the following behavior:

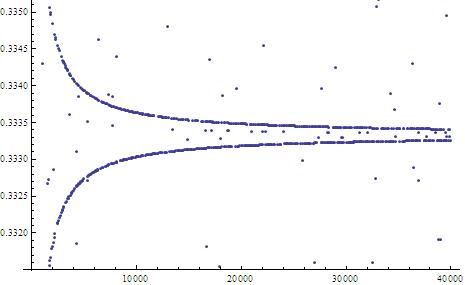
Similar behavior holds around the value $\frac{2}{3}$ .

Similar, but weaker, behavior occurs around the values $\frac{1}{5} \textrm{ and } \frac{1}{7}$ :

References & readings

Christian Aebi & Grant Cairns. Catalan numbers, primes and twin primes. (cairns_catalan)
Campbell, D. The Computation of Catalan Numbers. Math. Mag. 57, 195-208, 1984
Steven Finch (March 28, 2007)Central Binomial Coefficients (central_binomial_coefficients_finch)
Tom Davis (2006) Catalan Numbers (catalan_numbers1)
David Fowler, The Binomial Coefficient Function. The American Mathematical Monthly, Vol. 103, No. 1 (Jan., 1996), pp. 1-17.
W. Sander, A Story of Binomial Coefficients and Primes, The American Mathematical Monthly, Vol. 102, No. 9 (Nov., 1995), pp. 802-807
Keith Ball (2006). Strange Curves, Counting Rabbits, & Other Mathematical Explorations. Princeton University Press. ISBN-13: 978-0691127972

Tags: Catalan number, prime number, pseudo-prime

Should we jettison the one size fits all math curriculum?

Posted by: Gary Ernest Davis on: May 12, 2011

In: Uncategorized
1 Comment

I will address college and university mathematics and not – yet – school mathematics.

The nature of the school mathematics curriculum, K-16 – is a major issue that needs urgent re-vamping, but today I want to focus on tertiary mathematics.

I want to focus on a report from the Times Higher Education supplement that was brought to my attention through a tweet from Nalini Joshi (@monsoon0).

Nalini Joshi

Nalini is Professor of Mathematics at the University of Sydney, Australia (where “Professor” means “Full Professor”), Chair of Applied Mathematics , Director of the Centre for Mathematical Biology, former Head of the School of Mathematics and Statistics (2007 – 2009), a Member of the Australian Academy of Science, and former President of the Australian Mathematical Society (December 2008 – September 2010).

She has reason, therefore, to be particularly concerned about an article that questions whether the mathematics education provided to students at colleges and universities throughout the world is appropriate for today’s students.

Here is the Times Higher Education article:

________________________________________________________________

Maths teaching seeks the formula for good graduates

12 May 2011

By Matthew Reisz

Report finds that a focus on content does not address students’ needs. Matthew Reisz writes

The teaching of mathematics in universities “may not be fit for purpose”, not least because it tends “to focus on content without a clear idea of what can be done with it”.

This is among the conclusions of a report that says universities risk leaving graduates ill-equipped to apply their mathematical training in the “real world”.

The analysis, which expands on an HE Mathematics Curriculum Summit run by the Maths, Stats and OR Network and the Institute of Mathematics and its Applications earlier this year, calls for “a more flexible approach to meet employer needs”.

The summit at the University of Birmingham brought together heads of mathematics or their representatives from 26 universities offering maths degrees. The resulting report, published last week, spells out both challenges and possible solutions.

One discussion group focused on the knowledge and attributes that maths students must possess to be allowed to graduate.

There was “considerable consensus” about the core areas and essential graduate attributes such as problem-solving, flexibility, enthusiasm for the subject – and the ability to communicate mathematics.

The last of these came under scrutiny in another discussion group.

Participants acknowledged that some maths students had “low social ability” and chose the subject “specifically to get away from having to present through long-form written and oral communication”. However, they also thought that universities should address these deficits.

Institutions offering maths degrees had “a duty and a necessity to meet students’ career aspirations”, which, the report says, includes developing graduate skills in presenting and other forms of communication. The report recommends that students be required to gain such skills and that universities help them to do so by, for example, providing maths support centres that encourage students to “work collectively”.

Even more contentious was the issue of students learning to handle new problems, which is vital because in many areas of employment, graduates “will be tackling unfamiliar problems”, the analysis notes.

Both modularisation and the rote learning encouraged by current assessment methods could add to students’ unease in novel situations.

More useful would be for lecturers to act as role models in “trying to solve unfamiliar problems, particularly ‘dirty’ problems with substantial risk of failure”.

The report calls for “a coordinated voice” and less anxiety about the demands of the Quality Assurance Agency, arguing that “if we are clear enough about what we want to do with our students, the QAA will be happy for us to do what we like”.

It also cautions academics not to project their own ambitions – namely a career as a mathematician – on their undergraduate students and to design each curriculum to meet the “aspirations of those people who will study that curriculum”.

More specific recommendations include “the development of a bank of industry-based problems” and further reflection on the difference between rigorous proof and ways of approaching unfamiliar real-life scenarios that might yield useful answers.

matthew.reisz@tsleducation.com

________________________________________________________________

The Department of Mathematics in which I work had two developing strengths when I arrived: mathematics education and computational mathematics.

Mathematics education has since been hived off into a different area of the University, and computational mathematics has gone from strength to strength.

It is fair to say that my current Department has a very strong national and international reputation in computational mathematics, and partners with engineering, physics, biology, chemistry and oceanography in developing computational science as a discipline.

It is no surprise therefore that our graduates tend, in the main, to seek and obtain work in computationally intensive applied mathematical fields.

Three recent examples: graduate work at Harvard in biostatistics, data technician at the Broad Institute in Cambridge, scientist at the Naval Undersea Warfare Center in Newport, RI.

Students have written, or come back, to tell us what they appreciate about their undergraduate degrees.

The things they consistently mention are:

statistics
linear algebra
Programming:

Python

MATLAB

R

proficiency with LaTeX

The other thing they mention is an environment where they are encouraged to follow their own research interests, an atmosphere in which they were expected to talk about their work and present at conferences, and an environment in which shared experiences and group work are encouraged.

This sort of environment has been made possible through a substantial grant from the National Science Foundation.

This funding is due to expire in 2 years.

Because this academic atmosphere has fundamentally changed how we educate our students, we need to find ways and means of extending this into the future.

My department has one real outstanding strength: computational mathematics particularly, but not only,Â as it relates to partial differential equations.

We are discussing now how to develop strength in data science, for which students will need skills in mathematics, statistics, computer science, scientific visualization and scientific communication.

As a small department we cannot be all things to all students.

We have some considerable strengths and are trying to develop new ones.

My feeling is that we need to focus on those things we can do well, to be up front with prospective students about what we do well, and re-design our curriculum so as to emphasize the skills and habits of mind we want our graduates to posses.

Simply “covering material”, no matter how well-intentioned, is not going to cut it any longer.

Providing students with an environment where they can work as a cohort on research problems of their choosing, where verbal and written presentation skills are emphasized, and where they are exposed to world class research conferences,Â is now critical to how we proceed in educating mathematics undergraduates.

Tags: college, curriculum, mathematics, universty

Republic of Mathematics blog