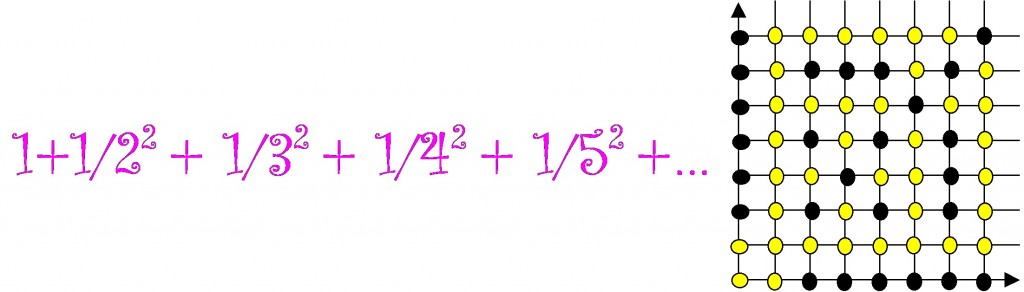Simple ratios, beautiful harmony: Karen X. Cheng
Posted by: Gary Ernest Davis on: May 11, 2011
Karen X. Cheng explores simple ratios and harmony:
The answer is Ï€^2/6: What’s the question?
Posted by: Gary Ernest Davis on: May 11, 2011
The Basel problem
One question that has as an answer was posed by Pietro Mengoli in 1644:
“What is the value of ?”
This became known as the Basel Problem, and Leonhard Euler solved it and announced his solution in 1735 when he as 28 years old.
Euler showed – at first not entirely rigorously – that
x
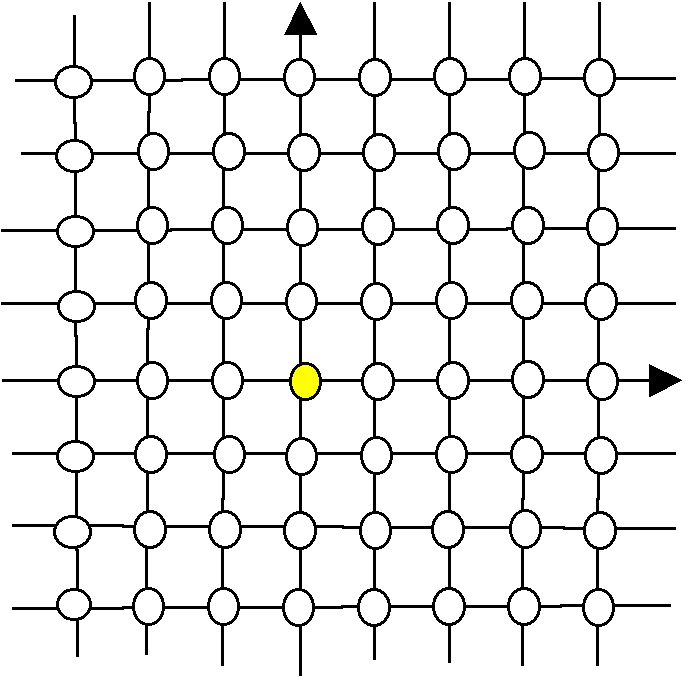
Visible lattice points
A lattice point in the plane is a point with integer coordinates:
We say a lattice point is visible from the origin
when the line segment joining
to
contains no other lattice points.
A question that has as an answer is:” What is the number of times we expect to choose a random lattice point until we get a point that is visible from the origin ?”
The reason for this is that the probability that a randomly chosen point is visible from the origin is , and so choosing a random lattice point is like flipping a weighted coin that comes up “VISIBLE”
of the flips and “NOT VISIBLE
of the flips. The waiting time until a visible point is therefore given by a geometric distribution and is just the reciprocal of the probability of choosing a visible point.
Co-prime integers
The lattice points that are visible from the origin are exactly those with
having no common factors (that is, being co-prime).
So is also the waiting time until two integers chosen at random are co-prime.
Why this type of question?
The reason for asking what is the question, given a result, is that such questions stimulate one to find creative answers, an answer being a question that leads to the desired result.
A teacher, for example, can see relatively easily how much relevant mathematics a student knows by asking a question of this type.
Here’s a simple yet revealing question to ask people at all levels of mathematical attainment: “The answer is 10. What is the question?”
Try it on a few people, preferably in groups: the answers may amaze you.
I can guarantee people will try, and you and they will be amused by the different answers given.