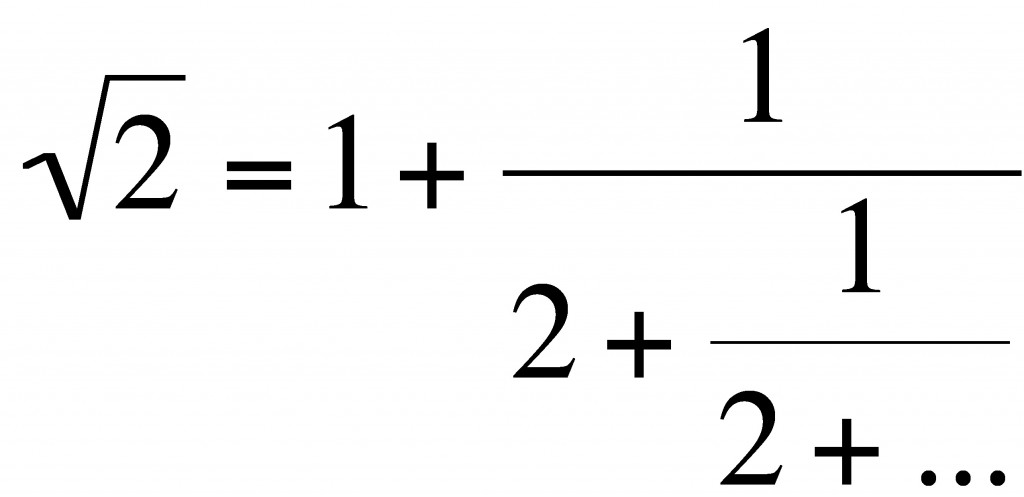Is rationalizing rational?
Posted by: Gary Ernest Davis on: May 3, 2011
Rationalize or get it wrong?
Text books and test setters regularly mark students wrong if they give an answer of to a problem.
A student is supposed to know, as part of mathematical convention, that should be rationalized to
.
This issue has been discussed before by @suburbanlion at SuburbanLion’s Blog and @jamestanton at Rationalising the Denominator, among others.
Marking a student wrong for not carrying out a rationalization like this is just BS (and I don’t mean “Bachelor of Science”).
And there is no such mathematical convention – it’s made up by people who write text books and set tests.
This issue came up again recently in #mathchat when @davidwees wrote: “I tell my students that people used to rationalize denominators b/c it made calculations easier” and “1.414…/2 is much easier to do than 1/1.414… without a calculator.”
My issue with what David wrote (and indeed with part of what James Tanton says in his video) is how, without a calculator, do we know that ?
Of course if someone told us that and we figured that
then we could probably be adept enough to calculate
by hand.
The field ![\mathbb{Q}[\sqrt{2}]](http://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Csqrt%7B2%7D%5D&bg=ffffff&fg=8E8778&s=0&c=20201002)
Numbers of the form where
are rational numbers (fractions) collectively have a remarkable structural property:
not only can we add, subtract and multiply such numbers and still get numbers of the same form (e.g. ), we can also divide such numbers and still get a number of the same form:
e.g.
Collectively, numbers of the form constitute a mathematical field, denoted by
– a structure in which addition, subtraction, multiplication and division (by non-zero numbers) is always possible.
From this perspective, rationalizing is just expressing the fact that the reciprocal of
is again in the field
.
What about rational approximations?
There are technical senses in which the continued fraction of a real number gives the “best” rational approximation to that number.
So how do we find the continued fraction for ?
We are looking for an (infinite) expression of the form :
where the are whole numbers.
Because the piece after
is less than 1, we see that
is the largest integer less than
, which is 1 (we know
because
).
This leaves so taking reciprocals we see that
.
This means that is the largest integer less than
.
In other words, , which means that
.
We know because
, so
.
Continuing in this vein gets trickier, because next we have to find the largest integer less than .
Because satisfies a quadratic equation we can use a cute trick to find the continued fraction for
.
Let’s write so that
.
Dividing by gives:
Taking this to a limit we get .
Since we get
.
By successively terminating this continued fraction we get the following rational approximations to .
This immediately gives us the following rational approximations to .
Newton and the Babylonians
Isaac Newton’s method for finding roots of functions, applied to the polynomial leads directly to a method for approximating
known to the Babylonians.
Using this method we start with an approximation – let’s start with
because its the first approximation from the continued fraction for
: it’s the integer part of
.
We then average to get the next approximation
.
We generate a sequence of rational number approximations to
where. at each step,
.
This gives us the following rational number approximations to .
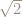 as a decimal
as a decimal
So now we know how to approximate by rational numbers, we can use the rationalization
to get rational approximations to
, but you see the absurdity – why bother? Just invert the rational approximations to
.
How about the decimal expansion of – where does that come from?
Decimal approximations to are usually obtained from the rational approximation from the continued fraction, of from the more rapidly convergent Newton’s (= Babylonian) method.
The record at the time of writing this post is is 1,000,000,000,000 decimal places due to S. Kondo & A.J. Yee in 2010.
The empirical evidence is that is normal in base 10, meaning that, to date, each of the digits appears with proprtion
, each pair of digits with proportion
, each triple of digits with proportion
and so on.
However no one yet has a proof of this.
Mathematics is an empirical science
Posted by: Gary Ernest Davis on: May 2, 2011
Many people – including some of my colleagues – like to argue that mathematics is an art, not a science, and that even if it is a science then it’s not like physics, chemistry or biology because it’s a deductive, not an empirical, science.
In the five videos below Doron Zeilberger argues a contrary point of view.