Republic of Mathematics blog

How many zeros are there in 2^n?

Posted by: Gary Ernest Davis on: April 23, 2011

In: Uncategorized
6 Comments

An old problem asks if $2^{86}$ is the highest power of $2$ whose base $10$ representation: $2^{86}=77371252455336267181195264$ , does not contain the digit $0$ .

For instance, the next $14$ powers of $2$ do indeed contain the digit $0$ :

$2^{87} = 1547425\textbf{0}491\textbf{0}67253436239\textbf{0}528$

$2^{88} = 3\textbf{0}9485\textbf{0}\textbf{0}9821345\textbf{0}68724781\textbf{0}56$

$2^{89} = 61897\textbf{0}\textbf{0}1964269\textbf{0}137449562112$

$2^{90} = 123794\textbf{0}\textbf{0}3928538\textbf{0}274899124224$

$2^{91} = 247588\textbf{0}\textbf{0}7857\textbf{0}76\textbf{0}549798248448$

$2^{92} = 495176\textbf{0}157141521\textbf{0}99596496896$

$2^{93} = 99\textbf{0}352\textbf{0}314283\textbf{0}42199192993792$

$2^{94} = 198\textbf{0}7\textbf{0}4\textbf{0}628566\textbf{0}84398385987584$

$2^{95} = 39614\textbf{0}81257132168796771975168$

$2^{96} = 7922816251426433759354395\textbf{0}336$

$2^{97} = 158456325\textbf{0}28528675187\textbf{0}879\textbf{0}\textbf{0}672$

$2^{98} = 31691265\textbf{0}\textbf{0}57\textbf{0}5735\textbf{0}3741758\textbf{0}1344$

$2^{99} = 6338253\textbf{0}\textbf{0}1141147\textbf{0}\textbf{0}7483516\textbf{0}2688$

$2^{100} = 126765\textbf{0}6\textbf{0}\textbf{0}2282294\textbf{0}14967\textbf{0}32\textbf{0}5376$

x

How many zeros?

Instead of asking the existential question “Is there a zero in the base $10$ representation of $2^n$ for $n\geq 87$ ?” we can ask the more quantitative question: “How many zeros are there in the base $10$ representation of $2^n$ .

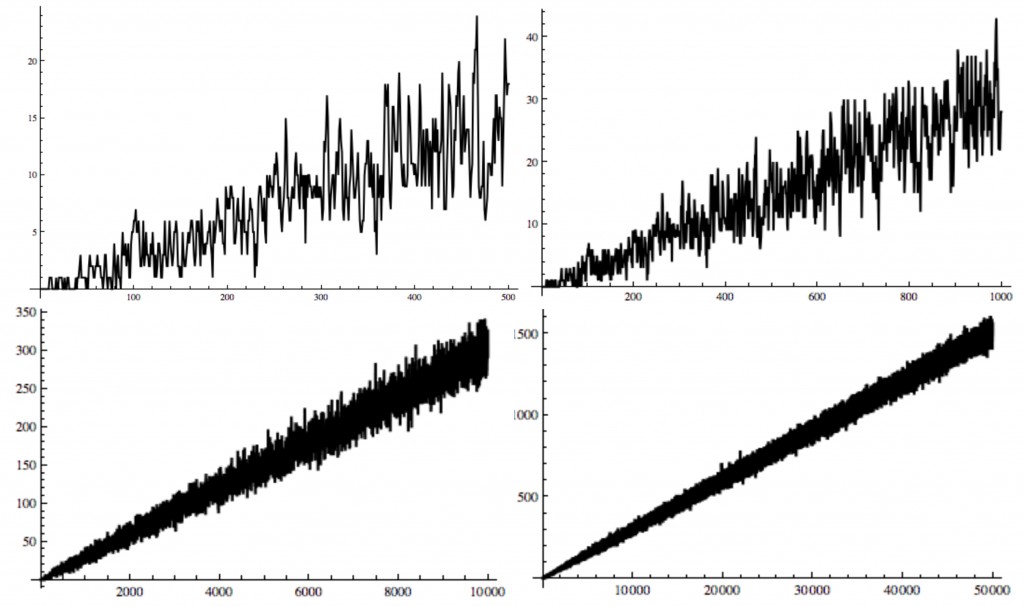
Here are plots of the number of zeros in the base $10$ representation of $2^n$ for $n$ up to $100, 500, 1000, 10000, 50000$ respectively:

We see, progressively, what seems to be oscillations around a straight line.

What could this straight line be?

And how large are the oscillations?

A straight line model

The number of digits of $2^n$ isÂ $\lfloor log_{10}(2^n)\rfloor +1$ , where $\lfloor x\rfloor$ is the integer part of $x$ .

Neither the first nor last digit of $2^n$ is $0$ , so there are $\lfloor log_{10}(2^n)\rfloor -1$ digits of $2^n$ that can be $0$ .

If we assume that all $10$ digits $0,1,\ldots 9$ are equally distributed among these $\lfloor log_{10}(2^n)\rfloor -1$ places then we expect to see about $n\frac{log_{10}(2)}{10}$ zeros in base $10$ representation of $2^n$ for large enough $n$

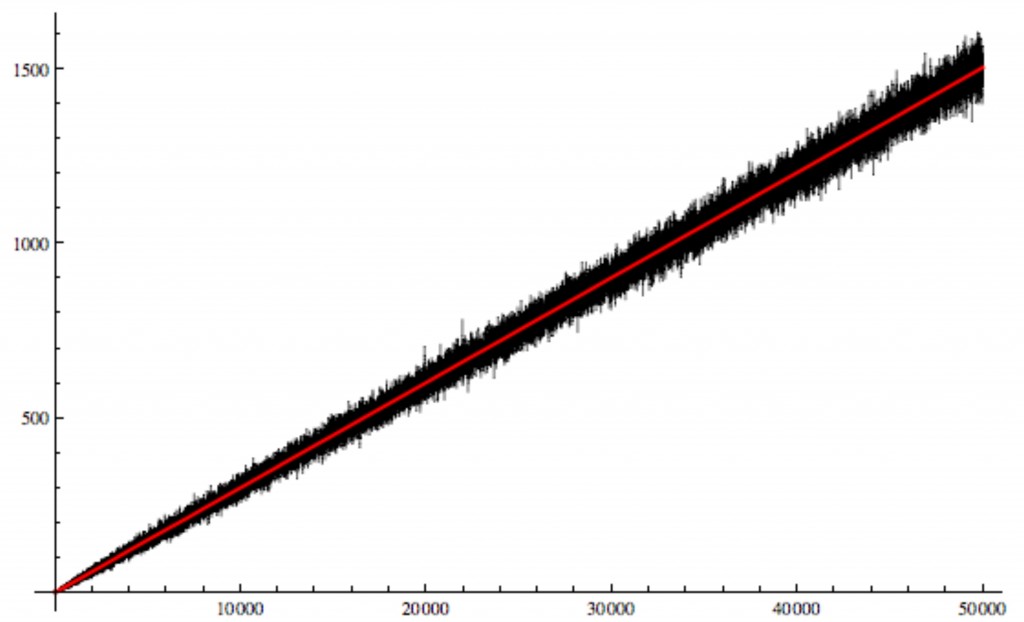
So we take as a linear model for the number of zeros in base $10$ representation of $2^n$ the quantity $n\frac{log_{10}(2)}{10}\approx .030103n$

To get a visual feel for how this fits let’s plot the actual number of zeros along with this linear model:

The nature of the “error”

We now have a statistical model for the number of zeros, $Z(n)$ in the base $10$ representation of $2^n$ :

$Z(n)=n\frac{log_{10}(2)}{10}+\epsilon_n$

where we will refer to $\epsilon_n$ as the “error” (meaning how much $Z(n)$ differs from the linear model).

How does the error behave?

In particular, how is it distributed?

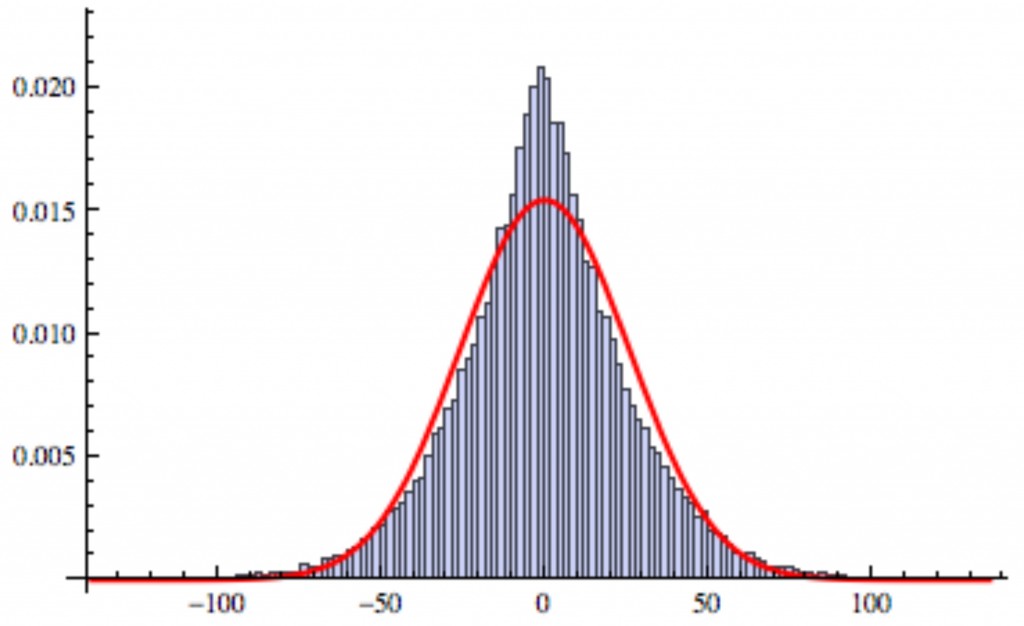
Below is a histogram of the error $\epsilon_n$ for $n\leq 50,000$ , together with a normal curve of the same mean and standard deviation:

We can see the the empirical distribution of the error is “peakier” than the normal distribution, and this is borne out by the kurtosis which is $3.9789 \approx 4$ , substantially greater than a kurtosis of $3$ for the normal distribution.

Plotting these histograms for various values of $n$ indicates that the variance of the distribution of the errors $\epsilon_n$ varies linearly with $n$ , or, what amounts to the same thing, the standard deviation varies with $\sqrt{n}$ .

Bounding the error

What we really seek is a bound on the errors sufficient to show that $Z(n)=n\frac{log_{10}(2)}{10}+\epsilon_n>0$ for large enough $n$ .

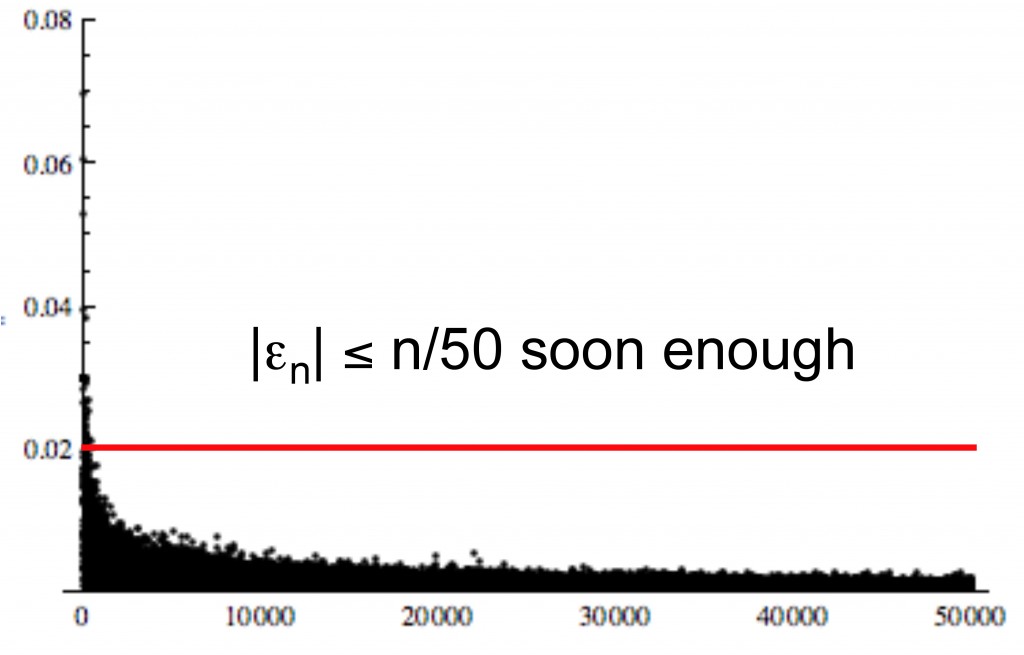
What does computation suggest?

Below is a plot of the size of the error $\vert\epsilon\vert$ divided by $n$ .

It appears that $\frac{ \vert\epsilon\vert}{n}\leq \frac{1}{50}$ even for quite small $n$ :

If this does hold good then $Z(n)\geq n\frac{log_{10}(2)}{10} - \frac{n}{50} >0$

So now we have a more precise statement: prove that $\vert Z(n)-n\frac{log_{10}(2)}{10}\vert\leq \frac{n}{50}$ for $n\geq 200$ .

Maybe techniques of higher order Fourier analysis (Higher-Order_Fourier_Tao) could be brought to bear on this problem since they are useful in proving other equidistribution theorems? Then again, just because Weyl’s polynomial equidistributionÂ theorem can be interpreted as a higher-order Fourier analysis application may have nothing at all to do with equidistribution of digits in $2^n$ .

Tags: equidistribution, powers of 2

Should mathematics teachers tell the truth?

Posted by: Gary Ernest Davis on: April 22, 2011

In: Uncategorized
8 Comments

Adults do not always tell the truth to children.

It’s common to let children believe there is a tooth fairy, that Father Christmas brings presents at Christmas time, or that a Golem defended the Jews in Prague.

Are there similar tales that mathematics teachers tell children?

Does mathematics have fibs, lies, and myths?

I will let you decide. But here, first, are some candidates for myths of mathematics:

(*) When trying to divide a circular region into 3 equal pieces, having made a radial cut from the center of the circle to the circumference, we know where to make the next cut.

Often we do not: we are simply guessing, or approximating by measurement, such as using a protractor marked in degrees. Of course, if we do know how to exactly construct an angle of 120 degrees then we can figure out how to make that next radial cut.

But we can push this a bit further: having a rectangular candy bar we know where to make the first cut to divide it into 3 equal pieces. Generally we do not, not unless we know the ancient Greek method for dividing a line into equal pieces using parallel lines. Be honest: do you know how to do this?

(*) We know how to add, subtract, multiply and divide decimal numbers.

No we do not – at least most of us do not. A procedure for doing arithmetic on decimal numbers was described in the paper: F. Faltin, N. Metropolis, B. Ross & G-C Rota, The real numbers as a wreath product, Advances in Mathematics 16 (3), 278-304 (1975).

This is not an easy paper and I would be tremendously surprised if many university or college instructors understood the ideas in it, let alone high school or elementary teachers. The problem, of course, is the infinite carrying we have to do when we try to do arithmetic operations on infinite decimal strings: without converting to fractions, how would you multiply 0.428571428571428571… by 0.384615384615384615… ?

(*) Decimal fractions are fractions written as decimals.

No they are not if we take the common school understanding of a decimal fraction as a finite decimal. With this understanding, decimal fractions are those fractions that, in lowest terms, have a denominator of the form $2^m\times 5^n$ .

(*) We know the numerical value of the area of a unit circle.

No we do not. We know a name for it: $\pi$ , and we know the decimal expansion of $\pi$ to any decimal places, but we do not, and probably never will, know the exact numerical value of $\pi$ as a decimal number; that is, its exact position on a number line.

(*) Polynomial algorithms are fast.

No they are not. Try a $\it{O}(n^2)$ algorithm on a large number of points, and see how slow it really is.

(*) We understand continuous functions.

No we do not. Continuous functions can exhibit hideous pathologies too horrible to even describe.

(*) Real numbers are well described as infinite decimals.

No they are not. We can only “describe” very limited classes of infinite decimals. Most behave more or less randomly.

(*) Randomness is a well-defined idea.

No it isn’t. We can test, through a bunch of sensible tests, if some sequence of numbers isn’t random, but we have no definition of “random”, despite its constant use in probability and statistics.

Then there are pedagogical myths:

(*) The idea of a variable doesn’t need explanation.

In fact, the foundations of mathematics do not contain “variables”. In that sense the idea of a variable is an extra mathematical concept imposed on the practice of mathematics. No “thing” can be variable, otherwise it would not be a thing. We say things like “the temperature is variable”. No it isn’t. The mercury in a thermometer varies, but we construct a “thing”, called “temperature” and then declare it varies. The most famous variable is “it”: it is raining, it is cold, it is hot, it is sunny, …

We often say “x is a variable”, but it isn’t: no matter how often we write it, it is still “x”.

Sometimes people say “x varies over the real numbers”. What does this mean? How is “x” varying?

Other people will say “x is a number”. Is it? If so, is it bigger than or less than 3?

Others will say “x is a container for a number”. If that’s the case then what is varying?

It’s a little confusing for a beginner. Variables are sophisticated ideas, not at all simple.

(*) Parallelism is an intuitive idea.

In fact much research shows that young children have great difficulty understanding parallelism. We might want to say the perpendicular distance between parallel lines remains constant, but it turns out that young children also have difficulty with perpendicularity.

(*) All students can see the lines in a grid.

In fact they cannot. Refer to this post for a fuller explanation.

(*) Students can see aspects of geometric figures if those features are pointed out to them.

Generally they cannot. Seeing is an active mental process, not just a mater of letting light fall on one’s eyes. Seeing geometricÂ properties and features is a process that requires active intelligence from a student, such as answering questions about a geometric figure when asked by others. Just “looking” is not enough to allow students to “see”.

There’s a lot more that could be included in a list of mathematical and pedagogical myths or fairy tales.

If you have any of your own, or are in violent agreement with mine, I would like to hear from you.

Shouldn’t we be doing our best to be truthful to students?

Tags: fairy tales, mathematics, truth