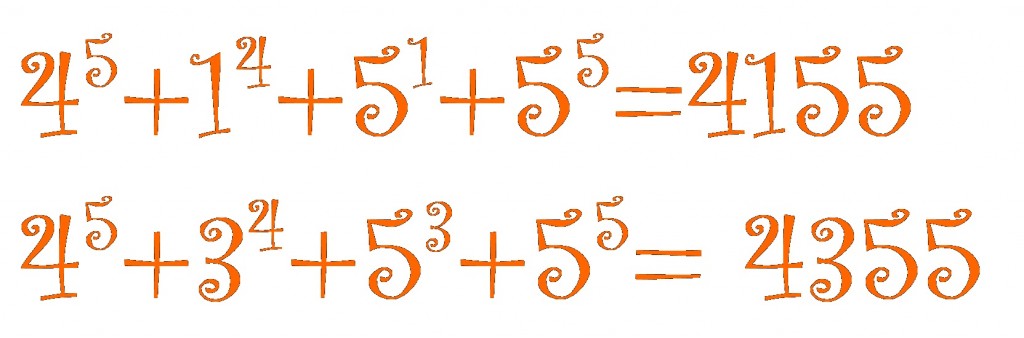What math teachers should know about memory, 2: working memory
Posted by: Gary Ernest Davis on: April 21, 2011
Mathematics teachers commonly complain that their students do not memorize facts, definitions and formulas.
In a previous post I described Hermann Ebbinghaus’s experiments on rote memorization, and his finding that memorization of nonsense syllables decays exponentially.
What we teachers of mathematics want is for students to recall, at least for the very next class, what came just before.
Ideally, education should set up long term – very long term – memories so that an educated person can recall basic facts and procedures many, many years after learning them.
A critical aspect of memory formation is focus of attention, and this is an important issue I will return to later.
Here I want to focus on an aspect of memory that we use as we carry out various tasks: working memory.
Memory research boomed in the late 1900’s, so much so that in 2000 a monumental handbook of memory research was published by Oxford University Press.
One of the best, most readable, introductions to the field of memory research, by two of the main contributors, is “Memory. From Mind to Molecules.” by Larry Squire & Eric Kandel.
Working memory
Using Wikipedia’s open source book creator I have pulled together a collection of Wikipedia articles related to this post: Working_Memory_WikiBook
Dissatisfied with inconsistent theories of short-term memory, Allen Baddeley & Graham Hitch introduced in 1974 a multi-component theory of working memory.
Roughly speaking, we can think of working memory as that aspect of memory we bring to bear on holding relevant information in the forefront of our minds as carry out more or less complex tasks.
Baddeley and Hitch proposed that working memory consists in broad outline of a central executive that coordinates information, and two “slave” systems, the phonological loop that stores and updates information about sounds, and a visuo-spatial sketch pad that stores and updates visual information.
Neurological studies have confirmed the Baddeley-Hitch model in broad outline (Oxford Handbook of Memory, pp. 77-92)
Cognitive load: why mathematics teachers need to know about working memory
The need for teachers of mathematics to know something about the functioning of working memory is clear: students must use working memory in order to solve mathematical problems.
The need for mathematics teachers to know details about working memory would be less were it not for the empirical fact that working memory is very limited in its capacity, and training in the use of working memory is generally not effective in increasing its capacity.
What this means in practice is that mathematics teachers need to be very aware of the cognitive load of a mathematical problem – the stress the problem is likely to place on individual student’s working memory.
The explicit concept of cognitive load originated with George Miller and was widely elucidated in problem solving by John Sweller.
In an earlier post I wrote about reducing cognitive load in algebra, and how John Sweller’s ideas, which I misunderstood for a long time, are very helpful in reducing cognitive load in mathematical problem solving.
Inappropriate language can stress working memory
I also wrote in an earlier post how the wording of a problem can significantly increase the cognitive load for a student.
The example used there was the following:
Sandy’s family does its laundry at a coin-operated laundromat. It costs $1.25 per load to use the washing machines and 25¢ per load to use the dryers for 10 minutes. Sandy’s family has 5 loads of laundry to do and each load will need to be in a dryer for 30 minutes. Which expression will give Sandy’s family the total cost of doing these loads of laundry?
A. ($1.25 + $0.25) × 3 × 5
B. [$1.25 + (3 × $0.25)] × 5
C. [(3 × $1.25) + $0.25] × 5
D. 3 × ($1.25 + $0.25) × 5
From the 2002 Washington Assessment of Student Learning (WASL) for Mathematics.
About half (49.9%) of more than 70,000 students who took the test were unable to manage the cognitive demands of this problem to select the correct answer. (Choice B)
About one-third (33.9%) of the students linked the information within the second sentence (Choices A and D) instead of linking information from the second sentence with information from the third sentence.
Students’ lack of prior experience with laundromats could be expected to impact their success rate.
What is really being tested by this problem?
Use of the pronoun it in the sentence, “It costs $1.25 per load to use the washing machines and 25¢ per load to use the dryers for 10 min,â€
Compounding & cognitive demands; “and 25¢ per load,†links the “25¢ per load†with the washing machine load until the end of the sentence -prior experience with laundromats signals the reader to interpret the sentence differently.
Spanish speakers, for example, may interpret the words to do as make.
Knowledge assumptions: a student may be familiar with wash clothes in English but not with the word laundry, and students whose families do laundry at home may not understand the word laundromat.
Load is usually first learned as a verb and when second-language learners read the word expression, they may, for example, think about what someone’s face looks like.
For many ESL students, English first names are not easily recognized; “What is a Sandy?â€
Intrinsically cognitively challenging problems
Empirically, some problems seem to increase cognitive load for many students, irrespective of how they are worded. The problem at the very beginning of this post is such an example.
Why this should be so is not at all clear.
The curious case of the number 3435
Posted by: Gary Ernest Davis on: April 17, 2011
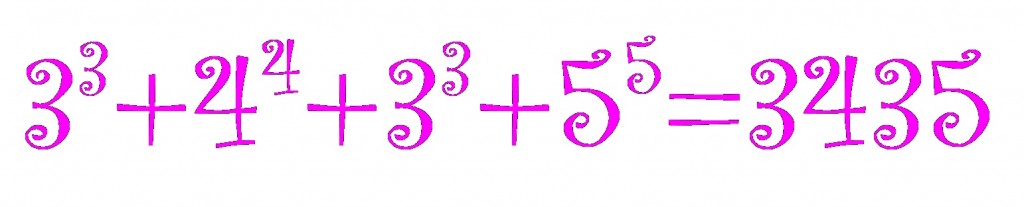 The (base 10) number
The (base 10) number has the curious property that
It shares this property with since
.
What makes even more curious is that it is the only number other than
that has this property.
To prove this we need to talk a little more exactly about what is this property.
The Münchausen property
Suppose is a positive integer and $latex d_k, see ldots d_1, patient d_0$ are the base 10 digits of n.
This means – a fact every elementary teacher of mathematics tries to get across to students when teaching place value – that
So given that (base 10) we form a new number:
The property we are interested in – sometimes called the Münchausen property – is that .
So we see that .
We will now see that there is no other positive integer for which
.
But first, store a little excursion into properties of the function .
Some properties of 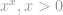 and a convention for
and a convention for 
We should have discussed what happens if a digit of the positive integer is
: because, then, we have to assign a value to
.
There is no magic way to decide how to assign a value to – we will use the continuity of the function
for
:
Because the limit of as
approaches
with
is
we assign the value
.
There is nothing magic about this – it just turns out convenient for our purposes here to have .
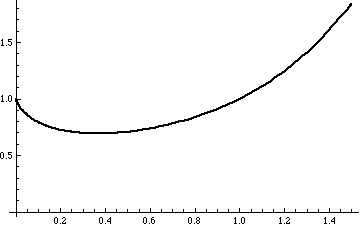
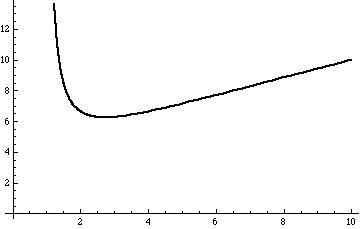
We can see the initially decreases as
increases, reaches a minimum value, and then increases.
We can see this from the derivative of
, which we can calculate by first taking (natural) logarithms:
so
and therefore
This is negative for and positive for
.
So, for non-negative integer values of the function
is non-decreasing: in fact, apart from
, we have
for all positive integers
.
The number of digits of a positive integer
For a positive integer the number of (base 10) digits of
is the floor of
, the largest integer less than, or equal to,
.
This means that the number of digits of is less than
.
An inequality for 
If the base 10 digits of the positive integer are
then:
for
- The number of digits of
is
So,
This says that cannot grow too big in terms of the number of digits of
.
An inequality for large 
We look at the behavior of the function :
The derivative of is
and this is positive for
.
So, for we have:
x
In other words, for we have
Positive integers  Â cannot be equal to
 cannot be equal to 
x
If is too big – for instance,
– then
cannot be equal to
.
The reason is that for we have
while
So we search through all positive integers up to and find no integers
with
other than
.
Variation on this theme
Suppose instead of forming as we did, we move the digits forward, with the first digit
moving around to be last: in other words, we form a new number
.
Do we ever have ?
Well, yes: we do for because
and
What if we move each digit forward two (with the first two cycling around to be be last and second last)?
References
van Berkel, D. (2009) On a curious property of 3435. Retrieved from arxiv.org: On_a_curious_property_of_3435 [This article provides the argument I have described in this post]
Perfect digit-to-digit invariant Wikipedia.org [In this reference another number is counted as a Munchausen number due to their using the convention 0^0=0]