A visual window on the apparently random digits of π
Posted by: Gary Ernest Davis on: February 28, 2011
The digits of π
Of course, the digits of Ï€, namely 3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 8, 9, 7, 9, 3, 2, 3, 8, 5,…, are not random.
Ï€ is the area of a circular region of radius 1, and is a perfectly well defined real number. We just don’t happen presently to know more than the first 2.7 trillion or so digits.
However, in many senses the digits of π behave as if they were random.
For example, each of the digits 0, 1, 2, … , 9 appears, so far, just the right proportion of the time, namely 
This property is known as being simply normal. Although it is suspected π is simply normal, no one has yet been able to prove it.
Strictly speaking, since we are looking at the decimal digits of π, this should be called simply normal base 10.
We could write π as a number in base 2.
The digits of Ï€, base 2 are 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, …
It is, on the face of it, conceivable that Ï€ is simply normal in base 2, (meaning the o’s and 1’s each occur about half the time), but not in base 10, or vice versa.
A simple analogy with coin-tossing allows us think about the base 2 expansion of Ï€ = 11.0010010000111111011010101000100010000101101000110000100011010011000100110001100110001… (base 2) having what seem to be random digits.
If we imagine that in the base 2 digits of Ï€, a “0” is replaced by “T” and a “1” is replaced by “H” then we get the following sequence
H, H, T, T, H, T, T, H, T, T, T, T, H, H, H, H, H, H, T, H, H, T, H, T, H, T, H, T, T, T, H, T, T, T, H, T, T, T, T, H, T, H, H, T, H, T, T, T, H, H, T, T, T, T, H, T, T, T, H, H, T, H, T, T, H, H, T, T, T, H, T, T, H, H, T, T, T, H, H, T, T, H, H, T, T, T, H, T, H, T, T, T, H, T, H, H, H, T, T, T, T, T, T, T, H, H, T, H, H, H, T, T, T, T, T, H, H, H, T, T, H, H, T, H, T, T, T, H, T, T, H, T, H, T, T, H, T, T, T, T, T, T, H, T, T, H, T, T, H, H, H, T, T, T, T, T, H, T, T, T, H, T, T, T, H, H, … of H’s and T’s
We know, of course, that this sequence of H’s and T’s did not come from someone tossing a coin, but could it have? Is there some way to distinguish this sequence of H’s and T’s from one obtained by a random tossing of a coin?
The National Institute of Standards and Technology has batteries of test for randomness. Basically, a truly random sequence should pass all these tests. Passing the tests does not mean a sequence of numbers is random – it just means the sequence passed a bunch of randomness tests.
One dimensional random walks
Let’s suppose we place a chip on a number line at the number 0.
Now we toss a fair coin over and over.
Each time the coin lands H we take one step to the right of where we are on the number line. And each time the coin lands T we take one step to the left of where we now are.
Where we will be at any time is unpredictable: it is the result of a random sequence of H’s and T’s.
Every time the coin lands H let’s write down a “1”, and every time it lands “T” let’s write down a “-1”.
Then we get a sequence of 1’s and -1’s such as 1, 1, -1, -1, 1, -1, -1, 1, -1, -1, -1, -1, 1, 1, 1, 1, 1, 1, -1, 1, 1, -1, 1, -1, 1, -1, 1, -1, -1, -1, 1, -1, -1, -1, 1, -1, -1, -1, -1, 1, -1, 1, 1, -1, 1, -1, -1, -1, 1, 1, -1, -1, -1, -1, 1, -1, -1, -1, 1, 1, -1, 1, -1, -1, 1, 1, -1, -1, -1, 1, -1, -1, 1, 1, -1, -1, -1, 1, 1, -1, -1, 1, 1, -1, -1, -1, 1, -1, 1, -1, -1, -1, 1, -1, 1, 1, 1, -1, -1, -1, -1, -1, -1, -1, 1, 1, -1, 1, 1, 1, -1, -1, -1, -1, -1, 1, 1, 1, -1, -1, 1, 1, -1, 1, -1, -1, -1, 1, -1, -1, 1, -1, 1, -1, -1, 1, -1, -1, -1, -1, -1, -1, 1, -1, -1, 1, -1, -1, 1, 1, 1, -1, -1, -1, -1, -1, 1, -1, -1, -1, 1, -1, -1, -1, 1, 1,…
If we add these, successively, we get a sequence 1, 2, 1, 0, 1, 0, -1, 0, -1, -2, -3, -4, -3, -2, -1, 0, 1, 2, 1, 2, 3, 2, 3, 2, 3, 2, 3, 2, 1, 0, 1, 0, -1, -2, -1, -2, -3, -4, -5, -4, -5, -4, -3, -4, -3, -4, -5, -6, -5, -4, -5, -6, -7, -8, -7, -8, -9, -10, -9, -8, -9, -8, -9, -10, -9, -8, -9, -10, -11, -10, -11, -12, -11, -10, -11, -12, -13, -12, -11, -12, -13, -12, -11, -12, -13, -14, -13, -14, -13, -14, -15, -16, -15, -16, -15, -14, -13, -14, -15, -16, -17, -18, -19, -20, -19, -18, -19, -18, -17, -16, -17, -18, -19, -20, -21, -20, -19, -18, -19, -20, -19, -18, -19, -18, -19, -20, -21, -20, -21, -22, -21, -22, -21, -22, -23, -22, -23, -24, -25, -26, -27, -28, -27, -28, -29, -28, -29, -30, -29, -28, -27, -28, -29, -30, -31, -32, -31, -32, -33, -34, -33, -34, -35, -36, -35, -34, …
These numbers represent the place of our chip on the number line.
A sequence such of numbers like this, obtained by adding the successive 1’s or -1’s produced from a random coin toss, is called a one-dimensional random walk.
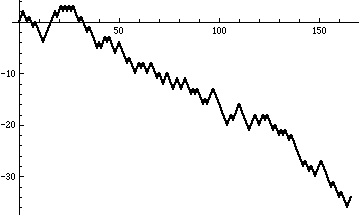
We can picture the random walk as a graph by plotting the numbers in the random walk (the position of the chip on the number line) versus their position in the sequence:
What sort of – possibly random looking – walk do we get if we use the base 2 digits of Ï€ ?
Here’s the result for approximately 330,000 base 2 digits of Ï€:
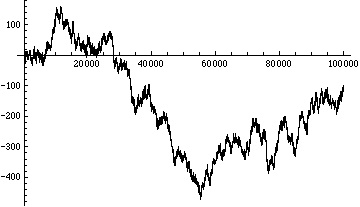
For comparison, here is a random walk constructed from a random sequence of 0’s and 1’s:
Of course just eyeballing the two graphs is not going to tell us if the base 2 digits of π seem to be random, but it does make us suspicious.
Also there are well known tests a random walk must pass: for example, for a truly random walk the average of the squares of distances of our chip from the starting point 0 after n steps must be approximately n.
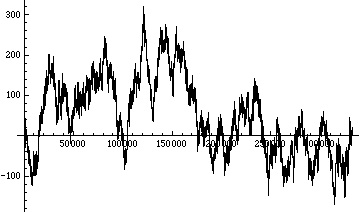
Two dimensional random walks
We can expand our random walk into the plane by starting at the point 
To simulate such a walk from the digits of π we would need 4 digits: one each to represent the 4 directions in which we can move.
To achieve 4 digits we can look at the base 4 expansion of π = 3.0210033312222020201122030020310301030122…
Using (arbitrarily) the digit 0 to represent moving one step to the right from our current position in the plane, 1 to represent moving one step to the left, 2 one step up , and 3 one step down, we get the following walk in the plane from the first 166,000 base 4 digits of π:
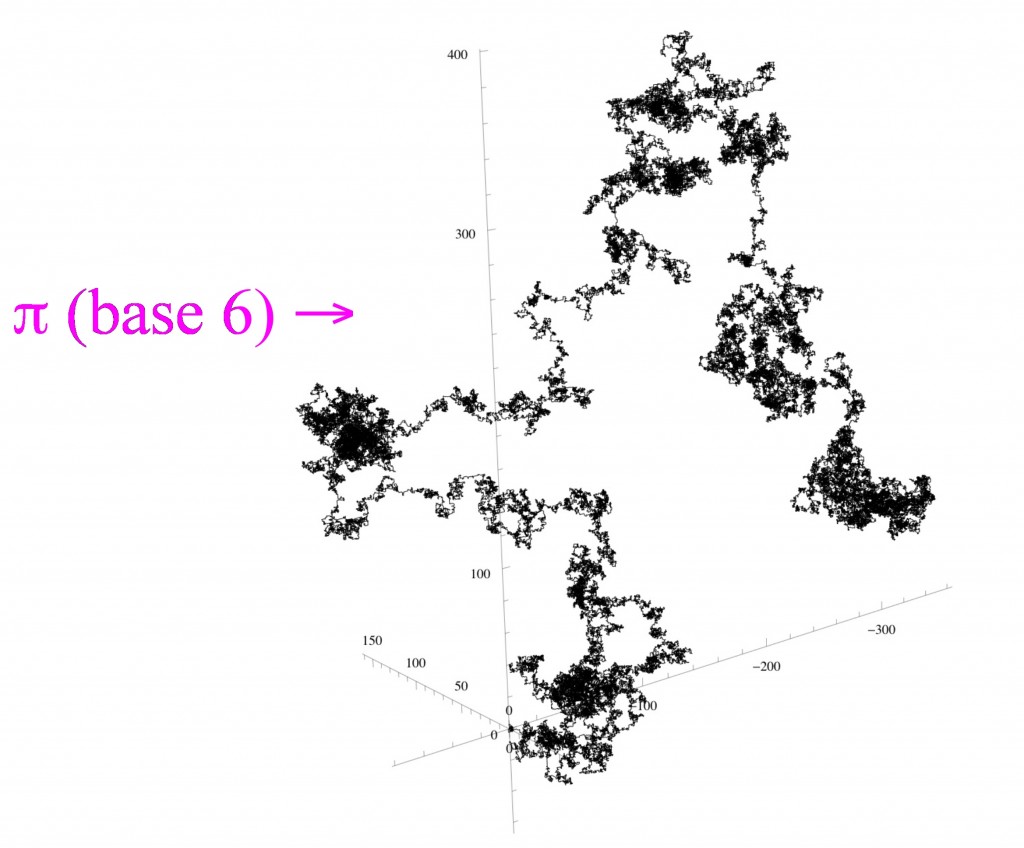
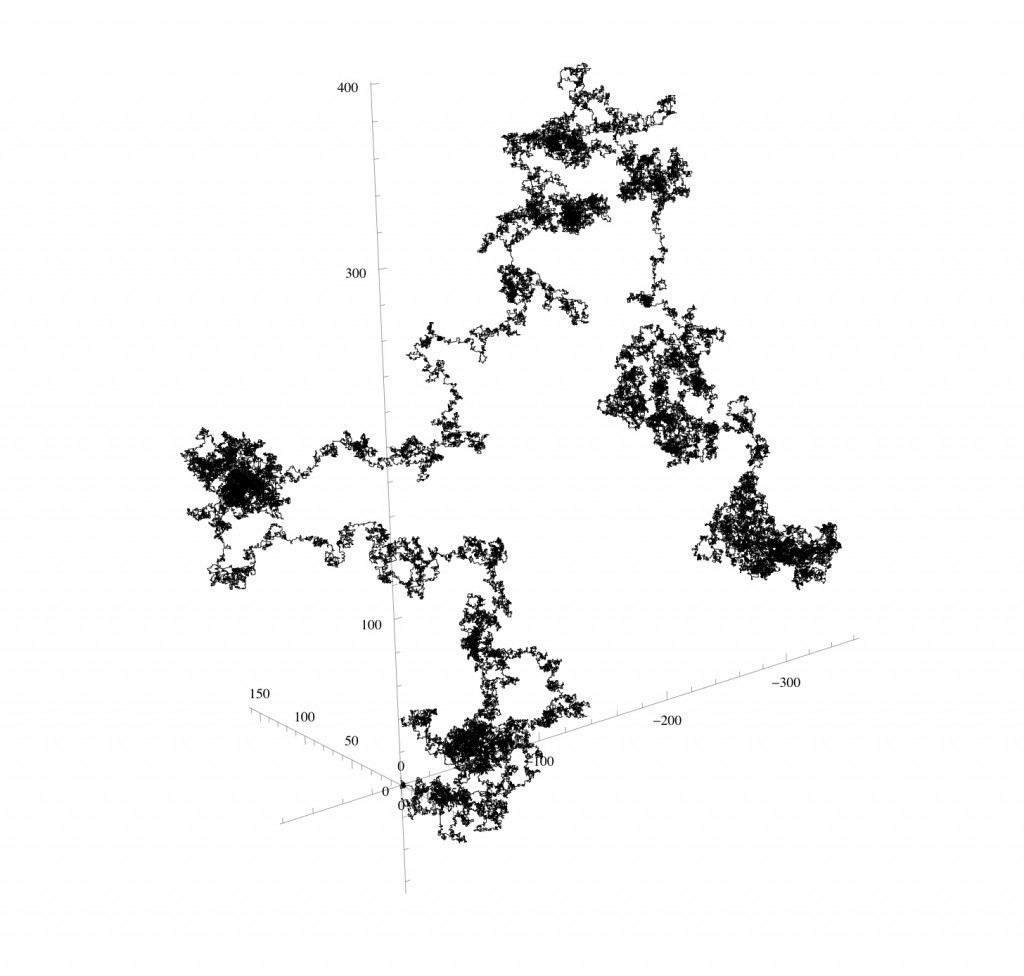
Three-dimensional random walks
In 3 dimensions, starting from the point 
To construct a walk from Ï€ we need 6 digits – one to represent each of the 6 directions – and so we look at the base 6 expansion of Ï€ =3.0503300514151241052344140531253…
Using (again arbitrarily) the digit 0 to represent a step of one unit in the positive x direction, 1 to represent a step in the negative direction, 2 a step in the positive y direction, 3 a step in the negative y direction, 4 a step in the positive z direction, and 5 a step in the negative z-direction we get the following 3-dimensional walk from the first 129,000 base 6 digits of π:
Five dimensional random walks?
To obtain a walk as we have been doing in which we use all 10 base 10 digits of π , we would need to construct a picture of a walk in 5 dimensions.
I, at least, do not know how to visualize this.
Perhaps a picture in a tiling of hyperbolic space might work?
Postscript
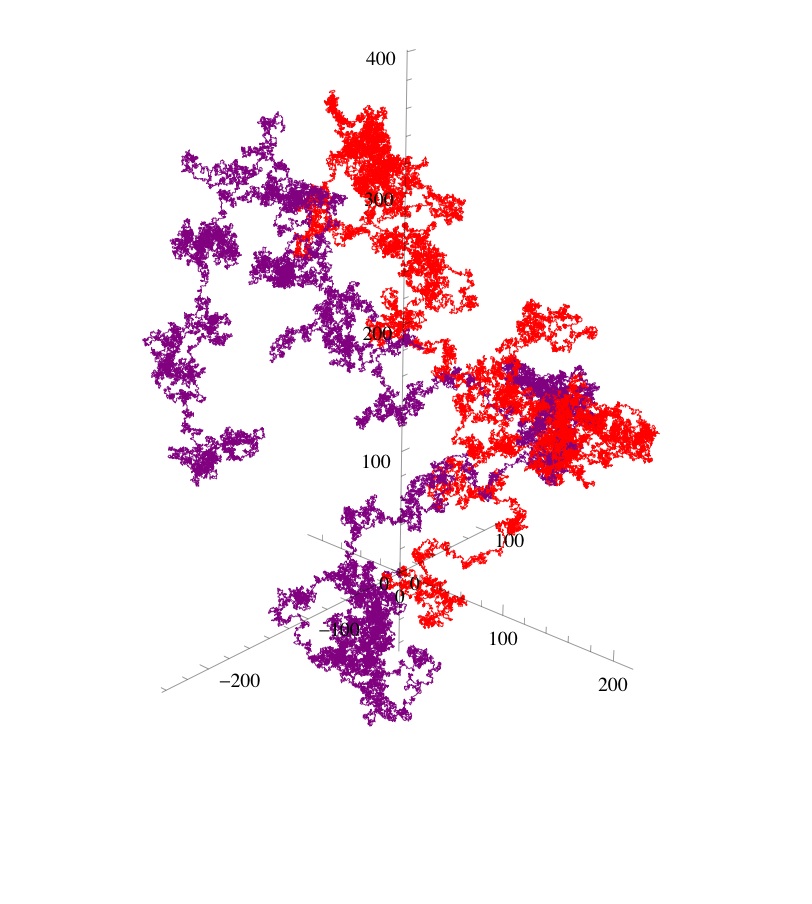
For comparison here is a walk constructed from the base 6 digits of e = 2.7182818284590452354 … = 2.4150520535242431231254044… base 6 – shown in red – with that from Ï€ – shown in purple:
Is my statistics class becoming a community of practice?
Posted by: Gary Ernest Davis on: February 25, 2011
