Save 30%, be 30% better off?
Posted by: Gary Ernest Davis on: February 22, 2011
A travel advertisement running, currently in the US, says you can save 30% on travel costs, and so be 30% better off.
Is that right?
How about 50% off?
To make it easier to think about, let’s think how much we would save if we got 50% off the price of something.
Suppose some item we wanted cost $100, and the salesperson said we would get 50% off.
This means we would pay only $50 when we thought we might have to pay $100.
So we could actually get 2 items for the $100 we originally intended to spend.
That is, we could get the 1 item we wanted, plus an extra 1 for the $100.
This, to me, means we are 100% better off.
What about 1/3 off?
Now let’s hone in on that 30% off.
Suppose we are offered 33% off the price of an item.
That’s pretty close to 
Let’s suppose the item was going to cost $90.
Now, with the discount of
That means we have saved half the cost of getting another one.
In other words, if we were prepared to spend $180 we would not get just 2 items, as we would have thought before we heard about the 
So whereas we thought we would get 2 items for $180 we will actually get 3 items.
This means we are one-half – or 50% – better off than without the discount.
So a
Because
So how much better off are we after a 30% discount?
What if an item costs $100 and we are given a 30% discount?
This means we only pay $70 for the item.
So if we were to spend $700 we would get 10 items after the discount.
Bu before the discount $700 would have only bought us 7 items, at $100 each.
So we are 
Even better than the advertisement stated.
It’s not often advertisers misrepresent the truth in your favor!
What would you do?
Posted by: Gary Ernest Davis on: February 21, 2011
In a previous post I explained how I have, over recent semesters, organized my teaching around projects and a more studio style of teaching.
I rely a lot on technology in teaching students to solve differential equations because for the most part that is exactly how they will solve them in their professional life, if indeed they ever come across them.
Bear in mind that the bulk of my students are engineering majors.
However, I do show them some elementary techniques for exact solution of differential equations, including the use of integrating factors for first-order linear equations.
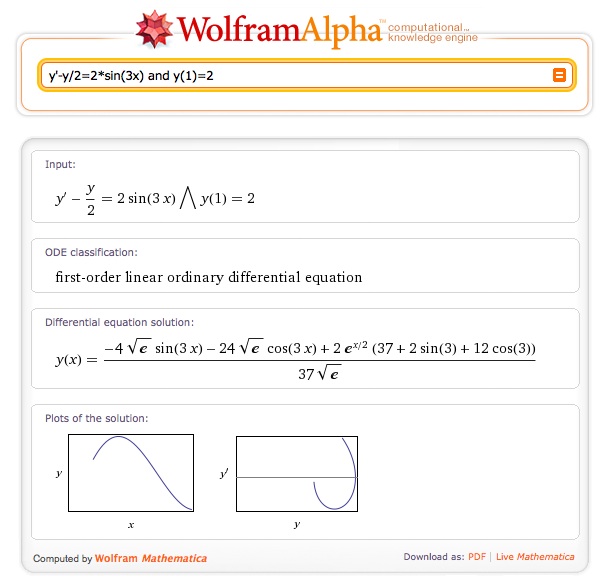
Here is an example I set for them recently:
So typically one writes the differential equation (*) in the standard form:
and multiplies (**) through by the integrating factor 
We then recognize the left side of (***) as 
This gives us the answer for 
Now here’s my dilemma in a differential equations course: rarely, if ever, can any of the students, all of whom have successfully completed calculus 2, recall how to calculate the integral 
Rarely, very rarely, someone will mention integration by parts, but then not be sufficiently proficient to actually carry out that procedure.
What should I do at that point?
What would you do?
I know I tell them to look up the integral in Mathematica (or MATLAB, or Maple).
I must admit the students are becoming more resourceful – many more of them are looking up the integral in Wolfram Alpha.
But then those who do that wonder why they cannot just put the original differential equation (*) into Wolfram Alpha to get an exact answer.
What would you say to them?
I am not trying to teach techniques of integration in a course on differential equations, nor am I trying to reinforce such techniques.
I am concerned with such fundamental issues as:
- What do the solutions of differential equations look like?
- How could you tell from the form of the differential equation?
- If there is an exact solution how does the formula determine the shape of the solutions, and could we have seen that better from the differential equation itself?
- How do we find accurate and stable numerical solutions to differential equations – especially systems of differential equations – for which there is no known exact solution?
I imagine that in 5 years time these – by then – practicing engineers will have forgotten every technique they ever supposedly learned for integrating, and for finding exact formulas for solutions to differential equations
What I hope they will recall is how to use technology to get a more or less accurate picture of a first-order differential equation, and reconcile that picture with the form of the differential equation. I hope they will recall that Euler’s method is a hopeless numerical method, and that there is too much loss of accuracy – both theoretically and machine accuracy – in its use. I hope they are able to interpret numerical solutions of systems of equations that model real-world phenomena.
But I could care less if they forgot how to integrate, when Wolfram Alpha can do it for them.
Or am I wrong?
