What would you do?
Posted by: Gary Ernest Davis on: February 21, 2011
In a previous post I explained how I have, over recent semesters, organized my teaching around projects and a more studio style of teaching.
I rely a lot on technology in teaching students to solve differential equations because for the most part that is exactly how they will solve them in their professional life, if indeed they ever come across them.
Bear in mind that the bulk of my students are engineering majors.
However, I do show them some elementary techniques for exact solution of differential equations, including the use of integrating factors for first-order linear equations.
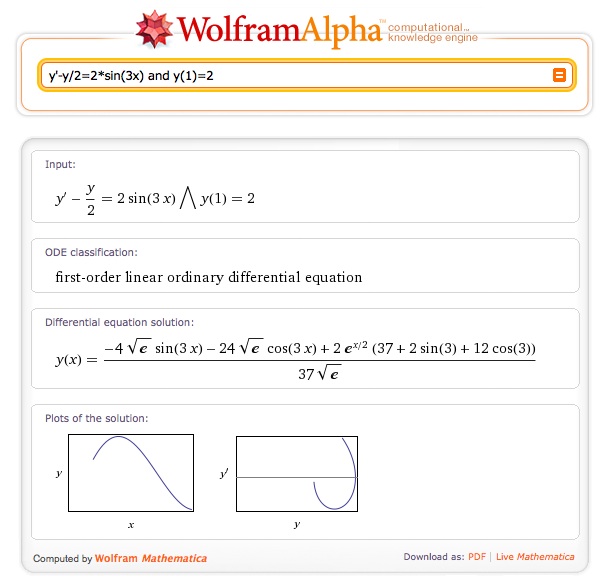
Here is an example I set for them recently:
……..(*)
So typically one writes the differential equation (*) in the standard form:
…….(**)
and multiplies (**) through by the integrating factor to get
…….(***)
We then recognize the left side of (***) as so integration gives us
.
This gives us the answer for so long as we can carry out the integration and determine the constant of integration from the initial condition
.
Now here’s my dilemma in a differential equations course: rarely, if ever, can any of the students, all of whom have successfully completed calculus 2, recall how to calculate the integral .
Rarely, very rarely, someone will mention integration by parts, but then not be sufficiently proficient to actually carry out that procedure.
What should I do at that point?
What would you do?
I know I tell them to look up the integral in Mathematica (or MATLAB, or Maple).
I must admit the students are becoming more resourceful – many more of them are looking up the integral in Wolfram Alpha.
But then those who do that wonder why they cannot just put the original differential equation (*) into Wolfram Alpha to get an exact answer.
What would you say to them?
I am not trying to teach techniques of integration in a course on differential equations, nor am I trying to reinforce such techniques.
I am concerned with such fundamental issues as:
- What do the solutions of differential equations look like?
- How could you tell from the form of the differential equation?
- If there is an exact solution how does the formula determine the shape of the solutions, and could we have seen that better from the differential equation itself?
- How do we find accurate and stable numerical solutions to differential equations – especially systems of differential equations – for which there is no known exact solution?
I imagine that in 5 years time these – by then – practicing engineers will have forgotten every technique they ever supposedly learned for integrating, and for finding exact formulas for solutions to differential equations
What I hope they will recall is how to use technology to get a more or less accurate picture of a first-order differential equation, and reconcile that picture with the form of the differential equation. I hope they will recall that Euler’s method is a hopeless numerical method, and that there is too much loss of accuracy – both theoretically and machine accuracy – in its use. I hope they are able to interpret numerical solutions of systems of equations that model real-world phenomena.
But I could care less if they forgot how to integrate, when Wolfram Alpha can do it for them.
Or am I wrong?



