Arc length: the sad and intriguing case of the length of a circle
Posted by: Gary Ernest Davis on: February 16, 2011
When I was a little fellow in secondary school I was puzzled by my teacher imagining string placed around a circle and straightening the string to find it’s length. I was also very uneasy about Ï€ as the ratio of the circumference of circle to its diameter.
For some time all I had was a vague feeling of unease about π and lengths of circles.
 Then, at about age 16, I read Godfey Hardy’s “A Course of Pure Mathematics” in which, as I recall, he stated that in order to find the length of a circle we first had to show that a circle HAD a length.
Then, at about age 16, I read Godfey Hardy’s “A Course of Pure Mathematics” in which, as I recall, he stated that in order to find the length of a circle we first had to show that a circle HAD a length.
This, of course, presupposes an advanced mathematical concept: the length of a curved line, in the plane, or in space.
The reason this is an “advanced” concept is not because it is especially difficult, but because it is based on a mathematical definition, and not taken for granted as something that is perceptually obvious.
When I understood this, I knew why my teacher’s string straightening worried me: how did he know that the straightening operation preserved length, if he could not even say what the length of a curved line was?
Of course, my teacher took the string straightening exercise as his informal definition of the length of a curved line. But it seemed to me, even as a young fellow, that the basis of mathematical reasoning could not, or should not, lie in manipulating pieces of string.
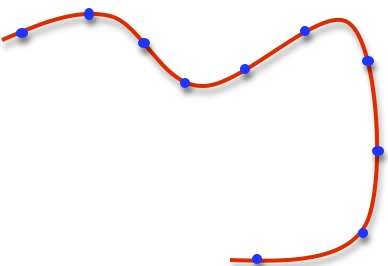
Well, the definition of the length of a curved line stems from taking a (finite) number of points on the curved line and joining them, in order, by straight line segments:
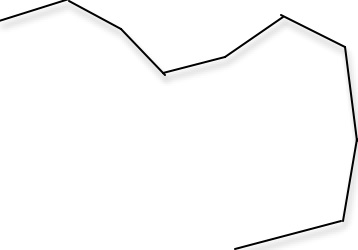
These straight line segments taken together, give us a broken line approximation to the curve:
Now we can calculate the length of the broken line by adding together the lengths of the individual straight line segments.
What is the length of the curve that the broken line approximates?
The idea is to take more and more points on the curved line, and see if the lengths of the corresponding broken lines approach some definite number.
If they do that number is called the length of the curved line.
In other words, we find the length of a curved line by approximating it by broken lines and seeing how the lengths of these broken lines behave.
In more advanced mathematics this involves a process of integration, in which the major difficulty is the idea of a limit.
It is VERY important that we choose points actually on and not just near, the curved line to join together. Even for a straight line segment, let alone a curved one, things can go badly wrong if we choose points close to, but not actually on the line whose length we are trying to find.
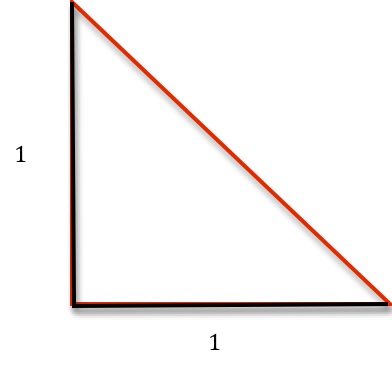
As an example, think about approximating the hypotenuse of the following right triangle by broken lines:
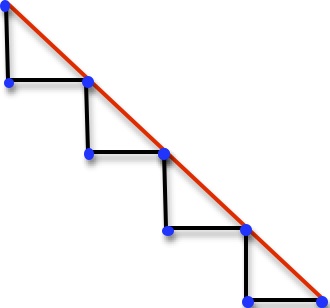
If we use points not exactly on the red line, but close, we get a length of the broken line that is not even close to the length of the red line:
If we repeat this process, halving the black line segments each time, we get a total length of the broken line equal to 2, at each step, but the blue dots get as close as we like to the red line.
It is very important, therefore, in obtaining broken line approximations to a curve, to find the length of the curve, that we choose endpoints of the segments actually ON the curve and not merely close.
Length of a circle
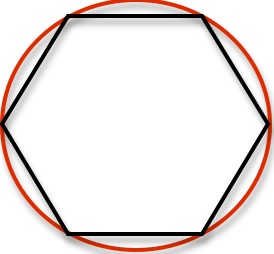
A circle is a curve, so how can we can we use this concept of length to find the length of a circle, say a circle of radius 1?
Of course we approximate a circle by polygons, with corner points placed ON the circle:
This is what Archimedes did to approximate the area of a circle.
But at each step of our approximation we are only ever approximating the length of the circle, not actually finding it.
So, at no stage do we ever actually know what is the length of a circle of radius 1.
Following Euler we now call this length 2Ï€. But that’s just a name.
Do we actually “know” what is the value of Ï€?
To paraphrase a well known and recent US President, it depends what we mean by “know”.
If we mean, can we exactly locate Ï€ as a decimal number, the answer is: “No”.
That is what is sad.
It is also tremendously intriguing: so much so that generations of mathematicians have worked on finding better ways to calculate approximate values for the length of a unit circle.
"This is a good way for me to learn math because I like art."
Posted by: Gary Ernest Davis on: February 14, 2011
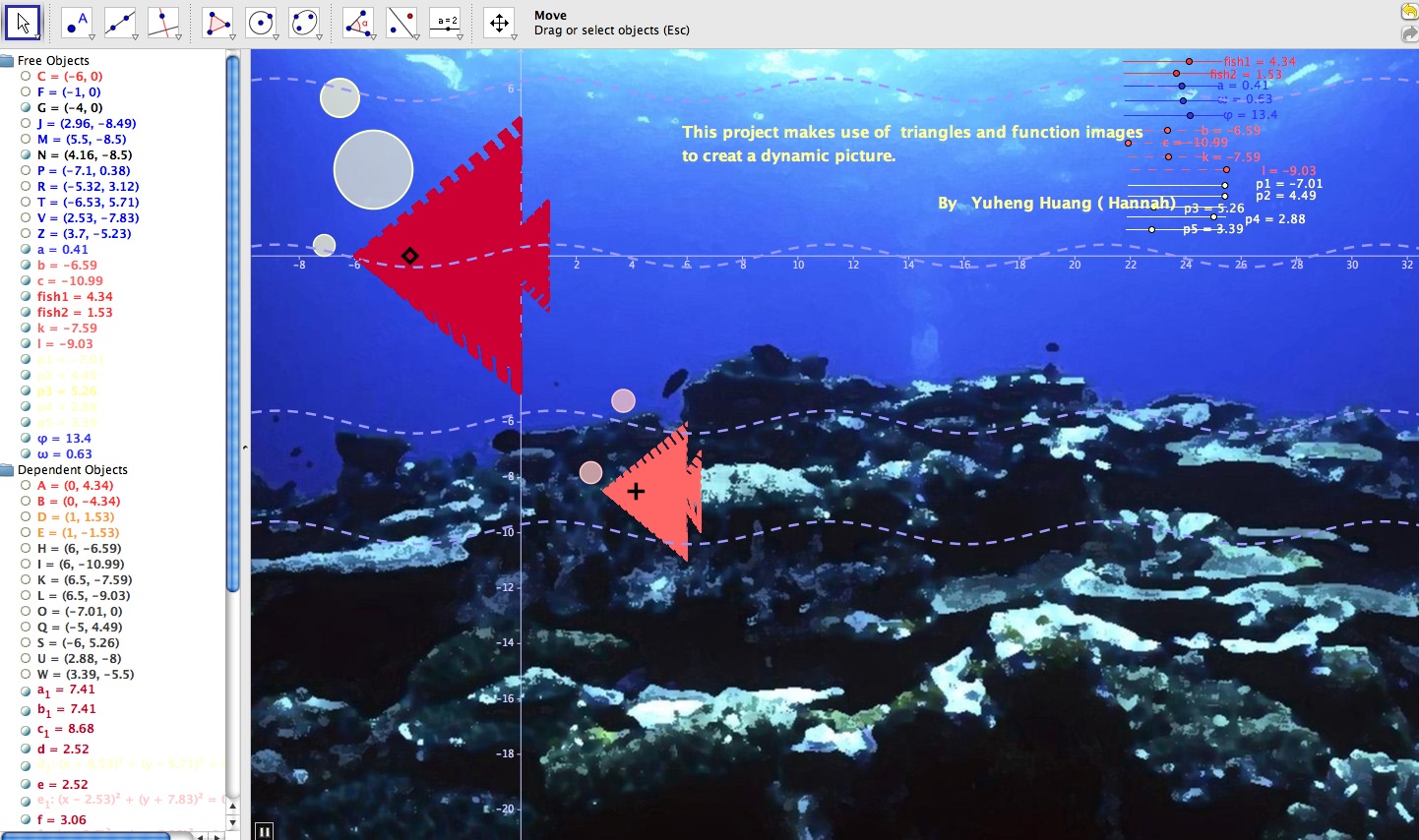
Michel Paul teaches mathematics at Beverly Hills High School in California. One of his students, Hannah, recently completed a GeoGebra project over winter break.
Hannah had never used GeoGebra before, and had recently arrived in the US from China.
Below is a screenshot of her GeoGebra project (click on the image for a larger version):
And here is a version of Hannah’s dynamic GeoGebra application.
Hannah explained how she came to create this GeoGebra applicaton:
“I am Hannah, the project “fish†is my works. Now, let me introduce how I create it.
Before I did it on the GeoGebra, I would draw my ideas on the paper.
“Interesting that she says she sketched it out first and then experimented with ways to implement it.
When I initially congratulated her on such a great project and asked her how she did it, she just laughed and said it took a long time.
I like her last statement, “This is a good way for me to learn math because I like Art.”
I had the kids in the lab on Friday, and I was watching what she was coming up with on her own while I was trying to help the others get up to speed. She was spontaneously creating all kinds of cool stuff.
This is an FST class (Functions, Statistics, Trig). The class is designed for students who have completed Algebra 2 but might not be ready for Analysis.
Hanna transferred to the school and was originally put in Analysis but was switched to FST because of language issues.
She had not been in the class more than a week or two when I assigned the project to do over winter break.
I had used GeoGebra previously with the other students, but Hanna had never seen it before, so I was hoping she wouldn’t feel overwhelmed. But she clearly took to it like … a fish in water. : )
The instructions for the project were simply to use GeoGebra to illustrate any of the concepts we had been studying about the various types of functions, such as quadratics, exponentials, step functions, transformations of functions, even and odd functions, and so on. Typical stuff.
I showed the kids how they could import pictures and create text boxes and sliders. I told them that they could be as creative as they wanted and to above all have fun with it.
The interesting thing is that we had not yet studied any trig – we are doing that now. So Hanna clearly had some prior background in trig in order to create this.”
- allowed and encouraged to follow their interests.
- given appropriate technological tools to help them.
- given time to complete longer projects.