What multiplication is … the central role of the distributive property
Posted by: Gary Ernest Davis on: January 7, 2011
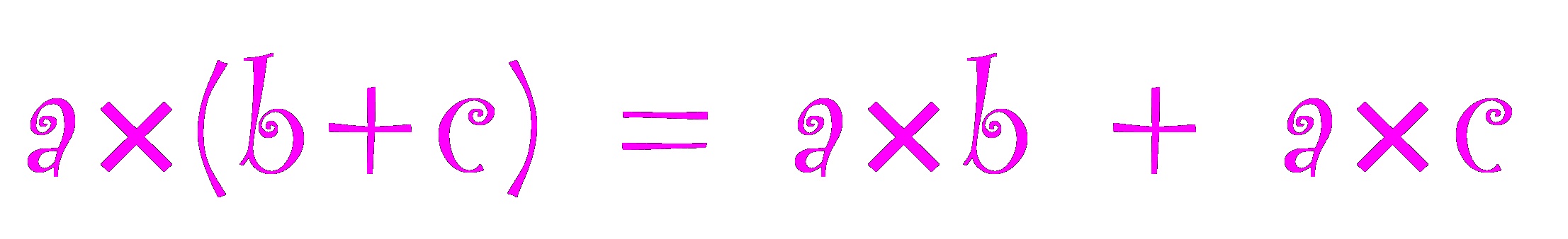 Tad Wattanabe raised some interesting points in his comments on the post Multiplication of whole numbers, and how we think about it.
Tad Wattanabe raised some interesting points in his comments on the post Multiplication of whole numbers, and how we think about it.
Part of what he said is that in Japanese texts, authors distinguish what multiplication IS as distinct from HOW TO multiply.
The issue of – psychological – models of whole number multiplication and repeated addition seem to raise the ire, if not the blood pressure, of many mathematics educators.
In this post I want to do something a little different: I want to demonstrate that there is one, and only one, candidate for multiplication of whole numbers.
As part of that demonstration it will become patently clear that multiplication is indeed repeated addition, by which I mean, as do most school teachers of mathematics, addition of a fixed number several times over, (as in but NOT as in
). See more about this in the postscript at the bottom of this post.
This is a very elementary demonstration, of a sort that most mathematics undergraduates experience in their degree studies.
In this demonstration, not all details will be filled in completely, but all can be, relatively easily.
The mathematics
First some notation.
The symbol will denote the set of all integers – positive or negative – and
will denote the set of pairs
of integers
.
A function is called bilinear if
for all integers
.
I claim: there is one and only one bilinear function for which
.
Here’s how we can establish this claim:
(1) First we will establish there is only one such bilinear function, by showing how it is determined. So suppose that
is a bilinear function with .
(2) For all integers we have
(by bilinearity) so .
Ditto, for all integers
.
(3) Let be a positive integer. Then
Similarly, if , we have
More generally (by induction)
(4) Similarly, for .
(5) For we have
If we have
More generally, (by induction) .
(6) For all integers we have
so
Ditto, for all integers
.
(7) Using (6) we can see readily that for
.
Hence is uniquely determined by its values for positive
as
(8) This establishes that there is at most one bilinear function
with .
(9) To see that there is a bilinear function
with we define
for positive integers
.
We extend the definition to general integers by defining
and
for positive integers .
It is usual to write .
This function is bilinear and .
(10) So there is indeed one and only one bilinear function
with .
That’s what multiplication IS; it is a a bilinear function  with
.
Moreover, we have shown that this unique bilinear function (normalized to give the value 1 at the point ) is just repeated addition, in the sense explained at the beginning of the post.
Some people have suggested that this inductively defined multiplication is not “really” multiplication; it is, they say, just a model of multiplication. This reminds me of Karl Gauss’s assertion that the complex numbers as defined in the Argand diagram did not capture his more general understanding of a complex manifold. That may well be so, since Gauss was a supremely gifted mathematician, yet no one since has ever found a need to, or indeed been able to, express an understanding of complex numbers other than that which is now standard in textbooks.
I suspect a similar situation holds for multiplication of integers.
Mental models
No one in their right minds imagines that is a way to tell school students what multiplication of whole numbers is.
So what do we tell them?
That, I feel, is at the heart of the arguments over multiplication as repeated addition (which it clearly is).
No one that I am aware of has a good cognitive root for multiplication of integers … with the possible and outstanding example of Peter Braunfeld and his ideas of stretchers and shrinkers.
But that’s a topic for another post (to follow…)
The distributive property
The bilinearity of multiplication is just the distributive property: .
This, together with the property , uniquely determines multiplication for integers.
So the demonstration above tells us that the most central, critical, and indeed defining, property of multiplication for integers is the distributive property.
This is the point that teachers need to emphasize when dealing with multiplication of whole numbers, because it is what tells us, together with , both what multiplication is, and how to calculate with it.
There are traps for an unwary teacher in using the most common form of modeling the distributive property through rectangular arrays. The danger is that adult teachers imagine young children see arrays in the same way they do. There is strong evidence that this is not so.
I discussed the distributive property and problems with rectangular arrays at length here.
Postscript on repeated addition
The issue of repeated addition is a constant source of irritation for some people. What seems to be the source of that irritation, so far as I can tell, is that the bilinear operation of multiplication is not an operation of repeated addition: rather it corresponds to an infinite number of repeated additions, one for each positive integer.
That, I would have thought, is obvious from the definition of multiplication. Multiplication by a number is determined inductively – via the distributive property (that is, bilinearity) – as
. This is repeated addition of the number
.
The common school statement of “multiplication is repeated addition” refers exactly to this situation: multiplication by a given integer corresponds to repeated addition by that integer. At worst, this is an abus de langage. One does not hear the phrase “muliplication is repeated addition” outside of school, at least not in my experience, and it is, as anyone who reflects on the matter will appreciate, a shorthand for what I wrote above.
School teachers, particularly elementary teachers, will often refer to subtraction as the inverse of addition.
Strictly speaking this is not correct: addition is a binary operation, giving a result for every pair of integers
.
Subtraction, as a binary operation, or partial operation on positive integers, is not the inverse of addition as a binary operation.
Nonetheless, for every integer addition of
does have an inverse which is subtraction of
.
To put it another way, every integer determines a unary, not binary, operation
. This unary operation has as an inverse the unary operation
.
Similarly, every integer determines a unary, not binary, operation
. That unary operation is indeed repeated addition of the number
If this is the essence of the long standing feud in the mathematics education community over multiplication as repeated addition then I think it is a rather silly feud, and could easily have been resolved through careful listening and a little flexibility of thought.
Elementary teachers, and a majority of middle and high school teachers, do not have the language of unary and binary operations, so they do not have that vehicle to express their thoughts. Mathematics educators, at least those with a degree in mathematics, should have such language to hand, and should be able to explain, in a productive and non-hectoring way, the connection between the two.
Practical Applied Mathematics (wherein multiplication is treated as repeated addition)
Posted by: Gary Ernest Davis on: January 6, 2011
Writing in the Newburyport Daily News, Regina Rita Ryan Allin of Louisville, Tennessee, recalled her memories of Joseph Woodwell Ledwidge Hale.
She wrote:
When I was in school, I was having problems with algebra and he (Hale) tutored me and gave me a book he had written, and signed, which was titled “Practical Applied Mathematics.” I still have the book, which was published in 1915, and I cherish it.
How wonderful that the author remembered with fondness a book on applied mathematics, and algebra, after so many years.
When I mentioned this story on Twitter John Rowland (@SofARMaths)tweeted:
Wonder if I can still get a second hand copy of Practical Applied Mathematics 1915…
I checked in Google books and sure enough, the entire book, published originally by the McGraw-Hill Book Company Inc. in 1915, is available for download as a pdf: Practical_applied_mathematics_Hale
The author wrote the book for trade and vocational schools, building on his experience with railroad schools. The book is intended to present mathematics as a useful tool to trade students.
Early in the book – page 5 to be exact – Hale introduces multiplication of whole numbers. Here is what he writes:
It is clear from this passage that Hale regards multiplication as simply shorthand for the process of repeatedly adding a given number: in short, as repeated addition.
What, if anything, does this illustrate or prove?
I think it proves nothing, but in the context of the entire book it illustrates something important: Hale was seeking a direct approach to mathematical topics so that his trade school students could use the mathematics as a tool. He did not introduce wrong thinking, or wrong methods of calculation, but often simply cut to the chase as if to say “this is how it is”.
Hale sets some multiplication problems as exercises. Some of these are straight arithmetical problems, with no other context. But the majority of them are practical problems likely to be encountered by trade students. These are not contrived problems, such as one often sees nowadays in textbooks, problems that pass for practical problems but are simply artificial situations invented by an author who knows little of the applications of mathematics.

 Hale gives approximate rules for many calculation. For example he introduces
Hale gives approximate rules for many calculation. For example he introduces as 3.1416 and he states the areas of polygons as a set of rules, without explanation. In this regard, his practice is not that much different from contemporary mathematics teachers.
He introduces some beautiful geometric problems in a practical trade setting:
Hale’s book is, in my view, a rich source of ideas and problems for all students of mathematics. He treats multiplication of positive whole numbers explicitly as repeated addition and that seems to work well for his purposes.
This does not mean multiplication SHOULD be taught as repeated addition, and certainly not that it should be taught only as repeated addition.
Hale’s book, as good as it is for the purpose he intended, is quite old and does not take into account many years in between of knowledge of how students learn mathematics (but, to be fair, neither do most contemporary text books, which are differentiated from Hale’s mainly in their exorbitant cost).
To the best of my knowledge no one has yet to come up with a model for multiplication that acts as a cognitive root -Â a way of thinking about a concept that, while not formally correct, nor complete in all details, is sufficiently powerful to allow students to use the concept, and to not have to throw their ideas overboard as their learning advances:
“A cognitive root is a concept that:
(i) is a meaningful cognitive unit of core knowledge for the student at the beginning of the learning sequence,
(ii) allows initial development through a strategy of cognitive expansion rather than significant cognitive reconstruction,
(iii) contains the possibility of long-term meaning in later developments,
(iv) is robust enough to remain useful as more sophisticated understanding develops.”