Happy mathematical new year: 2011 is the sum of 11 consecutive prime numbers
Posted by: Gary Ernest Davis on: January 1, 2011
- In: 2011
- 39 Comments
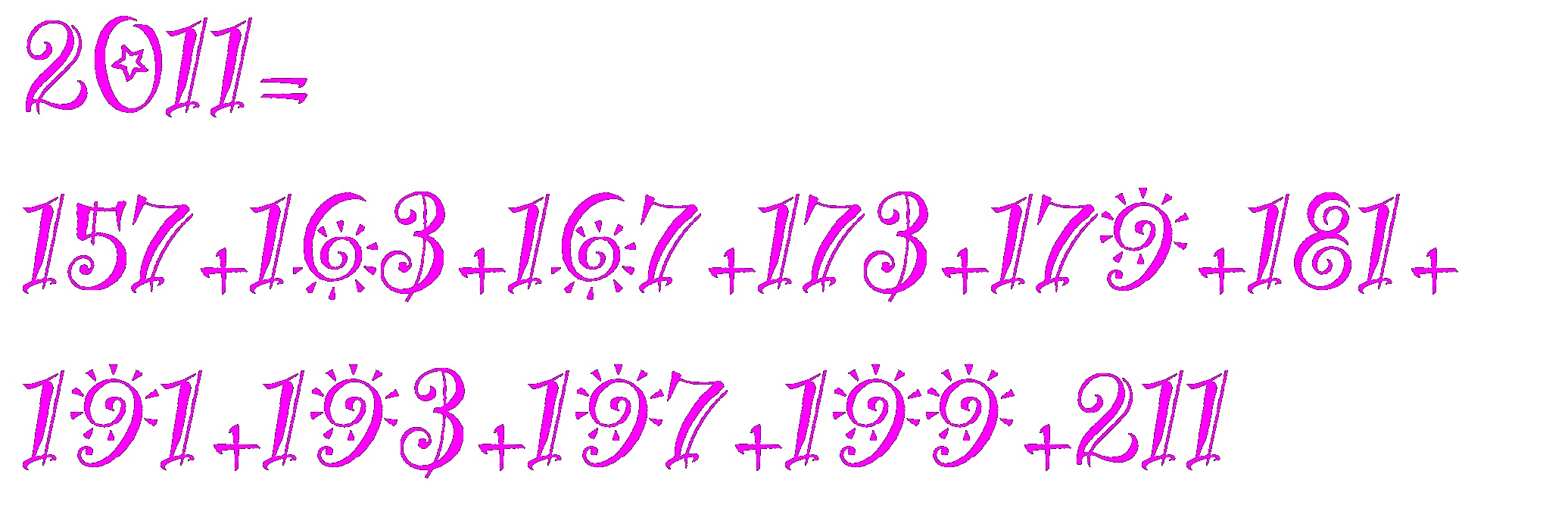xOn December 31, 2010 @mathematicsprof posted two interesting tweets:
@mathematicsprof 2011 is also the sum of 11 CONSECUTIVE prime numbers: 2011=157+163+167+173+179+181+191+193+197+199+211
x
Two prime numbers are “consecutive” if they follow one upon the other, in the collection of prime numbers. So, for example, 3 and 5 are consecutive prime numbers, as are 7 and 11.
These tweets, re-tweeted, attracted a fair amount of attention, deservedly so, because the second observation is both funny and thought provoking.
_____________________________________________________________________________________________________
Many people said to me they wished they had the “2011=157+163+167+173+179+181+191+193+197+199+211” on a T-shirt, so …. by popular demand I am happy to say that you can now purchase just such a T-shirt:
_____________________________________________________________________________________________________
I asked the question “Which prime numbers are sums of consecutive prime numbers” and David Radcliffe (@daveinstpaul) tweeted:
Primes expressible as the sum of consecutive primes: http://bit.ly/dKuh9S (2011 is an example!)
The link leads us to an entry in the On-Line Encyclopedia of Integer Sequencesâ„¢ in which there is some data on prime numbers that are sums of two or more consecutive prime numbers.
This On-Line Encyclopedia of Integer Sequencesâ„¢ entry includes Mathematica code to find such prime numbers.
The problem of finding prime numbers that are sums of two or more non-consecutive primes is a non-trivial computational exercise for school students and, it seems to me, one that many of them would find fun.
Here’s a variant of that problem, stemming from @mathematicsprof’s observation:
2011 is the sum of a prime number (11) of consecutive prime numbers.
Which prime numbers are a sum of a prime number of consecutive prime numbers?
Enjoy, and Happy New Year!
Postscript
The next year after 2010 that is a prime number and a sum of consecutive prime numbers is 2027 = 29+31+37+41+43+47+53+59+61+67+71+73+
79+83+89+97+101+103+107+109+113+127+131+137+139
but that year is not a sum of a prime number of consecutive prime numbers.
However, 2027 does have the curious and interesting property that it is prime and the sum of its digits 2+0+2+7=11 is also a prime number. It is the first year after 2003 that has this property.
The next year that is a prime number and a sum of a prime number of consecutive prime numbers is 2081 =401+409+419+421+431.
The following modification of Vladimir Orlovsky’s Mathematica code produces prime numbers that are a sum of a prime number of consecutive primes:
p = {};
Do[a = Table[Prime[i], {i, n, 100}];
l = Length[a];
k = 1;
While[Prime[k] < l + 1, b = Plus @@@ Partition[a, Prime[k]];
k++;
p = Append[p, Select[b, PrimeQ[#] &]]], {n, 1, 99}];
S =Union[Flatten[p]]
The first prime number that is a sum of two or more consecutive primes but is not a sum of a prime number of consecutive primes is 17 = 2+3+5+7
@mathematicsprof further tweeted on January 1, 2011:
2011 is also the sum of THREE consecutive primes 2011 = 661+673+677 . Can you write 2011 as the sum of 5, 7, 9, 11, 13, … primes?
This, of course, leads us to ask:
in how many ways can a prime number be written as a sum of consecutive primes?
(allowing, for convenience, a sum to have only 1 term, so that, for example 7 =7 can be written as sum of consecutive primes in only 1 way, whereas 5= 5 = 2+3 can be written as a sum of consecutive primes in 2 ways).
R packages that might be useful
People familiar with R might want to recode the above-mentioned Mathematica code in R.
Here are details of two packages that should prove useful in doing this:
Partitions: partitions
Primality checking: schoolmath
Multiplication of whole numbers, and how we think about it
Posted by: Gary Ernest Davis on: December 31, 2010
I want to take a – relatively minor – exception to Keith Devlin’s post, What Exactly is Multiplication?, on multiplication as repeated addition, and then largely agree with what he writes, with some amplification.
Multiplication is a defined notion for whole numbers and is provably commutative
Devlin claims that multiplication is not repeated addition and that “the mathematician’s concept of integer or real number multiplication is commutative: M x N = N x M. (That is one of the axioms.).”
I believe he is wrong on both counts.
First, both addition and multiplication are defined notions on the integers, rational numbers, and real numbers. For the positive integers, multiplication is defined recursively as 
This makes multiplication exactly repeated addition.
Secondly, the commutative property 
It is an axiom for general structures such as rings or fields, where one posits a commutative operation of multiplication, but it is a provable property of the defined notion of multiplication of natural numbers.
Why we shouldn’t (only) think this way
One can prove properties of multiplication from the definition of multiplication of natural numbers – essentially defined as repeated addition – but, as Devlin points out very well, this is not a productive or creative way of thinking about multiplication.
The inductive definition of multiplication of whole numbers is like a lawyer’s definition: it’s designed for safety reasons, to ensure that we are able, at some low level, to prove statements we make about multiplication.
However, the legalistic inductive definition of multiplication is not really helpful in thinking in other ways about multiplication as an operation on whole numbers.
What is needed for younger students is a sound psychological – not simply logical – way of thinking about multiplication.
Concept definition and concept image
Keith Devlin is, to my mind, essentially blurring over the distinction between concept definition and concept image.
The inductive definition of multiplication is a concept definition and, as such, is a part of advanced mathematical thinking, as defined and elucidated by David Tall.
Defined notions are, in general, not especially suitable for younger students, who do not yet see the necessity for such rigor.
Much more importantly for students is what David Tall refers to as a cognitive root. This is a way of thinking about a concept that, while not formally correct, nor complete in all details, is sufficiently powerful to allow students to use the concept, and to not have to throw their ideas overboard as their learning advances:
“A cognitive root is a concept that:
(i) is a meaningful cognitive unit of core knowledge for the student at the beginning of the learning sequence,
(ii) allows initial development through a strategy of cognitive expansion rather than significant cognitive reconstruction,
(iii) contains the possibility of long-term meaning in later developments,
(iv) is robust enough to remain useful as more sophisticated understanding develops.”
An example of a sound cognitive root is the idea of a function as a machine with inputs and outputs.
A cognitive root is essentially a solid foundation for thinking about a concept that can be later modified, and made more rigorous, but which remains as a basis for understanding.
What is important for younger students is a solid concept image of multiplication, based on firm cognitive roots.
Devlin addresses this issue explicitly (but without the language of concept image and cognitive roots, when he writes:
“So what is my mental conception of multiplication? It’s a holistic amalgam of all the above and several variants I have not listed. That’s why I say multiplication is complex and multi-faceted. The dominant mental image I have is very definitely the continuous one of scaling, and I see all the others in terms of that. This means that my conception of scaling within this context is a very general one, that encompasses examples like my bags of apples. I can view the computation “3 bags each containing 5 apples gives 15 apples altogether” as “scaling” a bag of 5 apples by a factor of 3. In my experience, acquiring the concept of multiplication amounted to creating this mental amalgam – the amalgam that is my concept of multiplication.”
One problem we know the scaling concept of multiplication produces when fractions come into the picture is that scaling by (positive) whole numbers never produces a smaller result, yet multiplication by fractions less than 1 does produce a smaller result.
Students often take on board from the scaling notion of multiplication the idea that “multiplication makes bigger”. That is one danger of seeing multiplication as scaling, and is why this concept image is probably not a good candidate for a cognitive root.
Multiplicative thinking in my view is largely based around lots of units. Some things – for example, candies – come in bags, and having a certain number of bags of candies, each containing a fixed number of candies, is not a bad candidate for a cognitive root for multiplication.
When those unit “bags” are capable of being split we can see multiplication of fractions in much the same way as multiplication of whole numbers.
