Numbers and patterns in nature
Posted by: Gary Ernest Davis on: December 31, 2010
Do mathematically less able students unnecessarily complicate things?
Posted by: Gary Ernest Davis on: December 30, 2010
A few anecdotal experiences, separated widely in time and space, have led me to speculate that less able mathematics students might be unnecessarily complicating procedures and examples, to the point where the complication impedes their learning.
Guess my number
A colleague at the University of Melbourne in Australia told me, many years ago, about her experiences with students trying to guess a whole number she had in mind. The game, as I recall, was for students to have 10 guesses to identify a whole number between 1 and 1000 that she knew but the students didn’t.
Let’s say the number, unknown to the students, was 473.
One way to go about this might be to ask: ” Is the number less than, or greater than or equal to, 500?”
The answer would be: “Less than 500.”
Then a reflective student might ask:” Is the number less than, or greater than or equal to 250?”
The answer might be: “Greater than 250.”
So, now, this reflective student, with a good strategy to hand, would ask: “Is the number less than, or greater than or equal to, 375?”
The answer: “Greater than 375.”
Now the student halves the difference between 375 and 500 as best they can, and asks: “Is the number less than, or greater than or equal to, 437?”
The answer: ” Greater than 437.”
The student has now used up only 4 questions, and is honing in on the number.
“Is the number less than, or greater than or equal to, 468?”
“Greater than.”
“Is the number less than, or greater than or equal to, 484?”
“”Less than.”
“Is the number less than, or greater than or equal to, 476?”
“Less than.”
“Is the number less than, or greater than or equal to, 472?”
“Greater than.”
“Is the number less than, or greater than or equal to, 474?”
“Less than”
Is the number 473?
“Yes!”
This took the student just 10 questions!
Of course the halving strategy works because .
One does not expect that a student will have worked this out before hand, but what is it that students actually do?
My colleague observed that the students who were more mathematically able, as estimated by prior achievement in class, adopted strategies similar to this. They chose numbers easy to remember and seemed to try to maximize the information that each answer gave them.
The less able students, in contrast, seemed to choose numbers more or less at random and chose numbers harder to recall. For example, they might ask: “Is the number 279?” “Is it 123?” “Is it 457?” and then forget which numbers they had already asked about.
The less able students seemed to minimize the information they obtained at each guess, and chose numbers that were harder for them to recall.
Complicating programming
During a mathematical inquiry class with undergraduates, we were investigating random walks with memory on a rectangular grid.
We wanted to obtain empirical estimates of the average distance such random walks got from their starting point. To that end students worked in groups using different programming environments: MATLAB, Python, Mathematica, to get some empirical data.
I worked with two students in a group.
As we developed our algorithm the details were becoming a little complicated. I put it to the students that we needed to radically simplify our approach. One of the students objected to this strenuously, telling me that a good program was one that was complicated. When I quizzed him about this he stated that the instructor would be impressed by a complicated program, but not by a simple one. To no avail I pointed out that I WAS the instructor and I valued simplicity and clarity over complication.
Was this student – whose GPA was significantly below 3.0 – unnecessarily complicating his approach to problem solving by an attitude of “complicated is good”?
Choosing surfaces in multi-variable calculus
This past semester I taught multi-variable calculus and when discussing surfaces, contour plots, and gradient fields, got the students, in pairs, to choose their own surfaces to work with.
What struck me was how the distinctly less able students in the class, in terms of GPA and prior work, chose very complicated surfaces to work with, while the most able students chose much simpler examples.
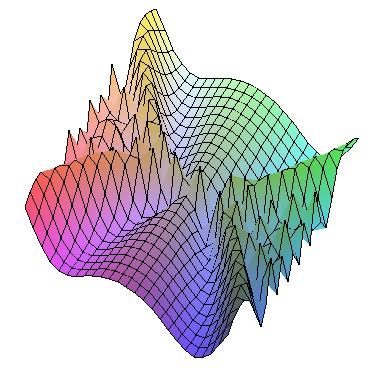
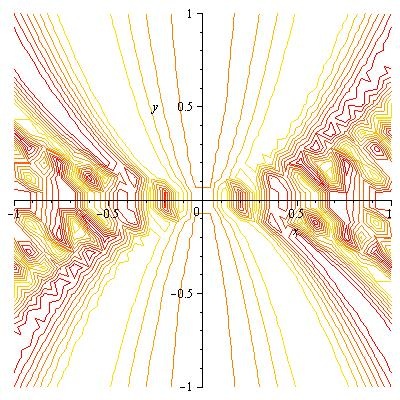
For example, two less able students working together studied the surface with the following pictorial representation:
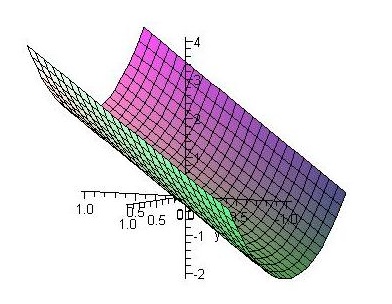
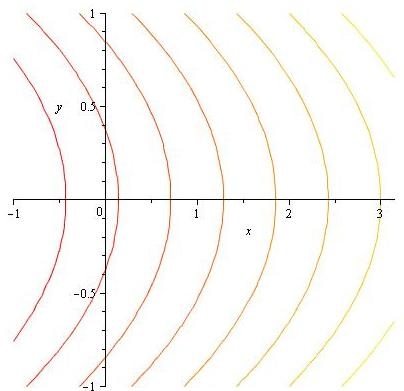
On the other hand, a highly capable student chose the surface with plot:
Is there a hypothesis here?
So long as we can come up with a measure or indicator of complication of examples – perhaps related to the information or lack of it that the example provides to a student – we could hypothesize that students with pre-existing lower mathematics achievement, estimated by tests and assignments, choose significantly more complicated examples than do mathematically more able students. This should be empirically testable.
I am very interested to hear about other clear examples of less able students choosing complicated examples to think about and more able students choosing simpler examples.
Cause and effect may be difficult to separate here, even if more able students do generally pick simple examples when learning a topic. Perhaps they are more able just because they DO choose simplicity as they are learning.
And just to cap it off …
Really simple math made complicated:
Postscript
I have been thinking about Peter Flom’s comment that ” … students who are mathematically able beautifully simplify things.”
I believe that to be true, and I also believe the work of Krutetsky showed that to be true.
However, the students in my mutli-variable calculus class did not simply fail to make things simple: they actually made them much more complicated. They deliberately chose examples of curves and surfaces with complicated and whistles, and then found those curves and surfaces hard to analyze analytically.
Their marked tendency to choose complicated examples impaired their ability to learn and analyze basic concepts related to these examples, such as the velocity, acceleration and curvature of a curve, and the gradient and directional derivatives on a surface.