To work in groups or not to work in groups? Is that the question?
Posted by: Gary Ernest Davis on: December 7, 2010
 This past Thursday and Monday #mathchat had a Twitter conversation on “Is groupwork or collaborative learning always possible in mathematics?”
This past Thursday and Monday #mathchat had a Twitter conversation on “Is groupwork or collaborative learning always possible in mathematics?”
As one would expect, much of the conversations revolved around whether and under what circumstances groupwork or collaborative learning was possible or desirable in mathematics.
Frequently, contributors discussed what parts of mathematical activity – for example, calculation – might be better carried out individually.
I think it fair to say that my attitude was mostly incredulous.
My comments on Thursday probably indicated as much.
Of course group work and collaborative work is always possible in mathematics,.
Of course sometimes people go off and do calculations by themselves, and at other times not.
What was, or is, the fuss all about?
Then today it hit me.
The discussion was not about group or collaborative work in mathematics.
Rather, it was about school students collaborating, or not, as the teachers saw fit, to solve exercise problems set by the teacher.
In other words, it was not about students doing mathematics, which of course is best done collaboratively.
Rather it was about students doing exercises.
Re-thinking the question
So, I feel the question is not whether groupwork or collaborative learning always possible in mathematics, but whether authentic mathematical activity is possible in school.
If it is, another question is whether it is possible in a significant number, even a majority, of schools.
Is authentic mathematical activity possible in schools?
Yes, it is. I have seen it.
My colleague Nigel Smith, now deceased, would engage his grade 5-8 students at Twyford School in Hampshire, UK in mathematical investigations where he himself did not know an answer, and did not know what route the students would take to a possible solution.
 And James Tanton, who teaches mathematics at St Marks’ school in Southborough, Massachusetts, engages his students in authentic mathematical investigations. Again, he does not always know where the investigation will go or what the students will produce, despite him having a Princeton Ph.D. in mathematics.
And James Tanton, who teaches mathematics at St Marks’ school in Southborough, Massachusetts, engages his students in authentic mathematical investigations. Again, he does not always know where the investigation will go or what the students will produce, despite him having a Princeton Ph.D. in mathematics.
Jim Tanton has written accounts of his work with students in the Mathematical Association of America’s Focus magazine, and regularly discusses mathematical problems on his website and on Twitter, where he is @jamestanton.
Is authentic mathematical activity possible in a majority of schools?
I suspect not.
Not unless a sea-change in teacher confidence, and what’s possible and valued in school mathematics occurs.
It does not require a critical mass of Ph.D. trained mathematicians teaching in schools.
What it does, and will, take is adherence to Lave and Wengers’ idea on legitimate peripheral participation.
Let’s think about the experience of school mathematics from this perspective.
Is school mathematical legitimate activity?
That is, would anyone involved in it – teachers or students – do it if they didn’t have to?
You bet they wouldn’t.
Well that’s not quite correct. Some people would. My former colleague Nigel Smith would – he loved thinking about mathematical problems and how to use those in his classes. James Tanton it seems to me is always thinking about mathematical issues and problems, and also how to use those in his classes.
Doubtless there are many other such mathematics teachers of whom I am unaware.
But many, many teachers I have known would not think a tap more about mathematics if they did not have to teach it.
Their mathematical activity is not legitimate. It is not driven by an inner compulsion, such as a potter has to make pots, or a knitter to knit.
Does school mathematical activity involve peripheral participation by students?
Overwhelming it does not.
Most teachers of mathematics are not masters to their apprentice students.
Their students do not participate in a community of learning with their mathematics teachers.
Students do not start peripherally, carrying out those simpler parts of a mathematical investigation and work their way along to where they are more expert.
Because – most mathematics teachers are not doing mathematics in their classes.
What they are doing is poring through text books to find exercises, or searching high and low for good class activities that might engage their students for a while – keep them productively busy.
The college experience
A Ph.D. in mathematics is no guarantee of legitimate classroom mathematical activity, and legitimate peripheral participation by students.
Just look at the thousands upon thousands of mathematics classes in colleges were students continue to carry out routine and – let’s face it – relatively boring and mind-numbing exercises.
Would the mathematics professor continue to work on these problems left to her or him self?
You bet they wouldn’t.
They might – and only might – go away and think about mathematical problems of an entirely different nature. A Ph.D. in mathematics will do that to you.
Teach mathematics more like pottery
 We are short changing our students by not allowing and encouraging our mathematics teachers to share a passion for mathematical problems
We are short changing our students by not allowing and encouraging our mathematics teachers to share a passion for mathematical problems
Students learn by initiation and by participation – peripheral at first, and more expert as time progresses.
Teachers, though, have to be doing authentic mathematics.
Teaching mathematics should be more like teaching pottery.
Then groupwork or collaboration is not even an issue.
Some curly questions on the base 3 digits of powers of 2
Posted by: Gary Ernest Davis on: December 6, 2010
Representing positive integers base 3
Positive whole numbers can easily be written in base 3, there where we allow the digits 0, 1, 2
For example: which we write as
, where the notation picks out the digits
and puts a subscript “3” to remind us that these digits need to be multiplied by appropriate powers of 3 and then added.
Using this notation and
because
Base 3 digits of powers of 2
How do the base 3 representations of powers of 2 look?
Here are the base 3 digits of the first 50 powers of 2:
| n | Base 3 digits of |
| 0 | 1 |
| 1 | 2 |
| 2 | 11 |
| 3 | 22 |
| 4 | 121 |
| 5 | 1012 |
| 6 | 2101 |
| 7 | 11202 |
| 8 | 100111 |
| 9 | 200222 |
| 10 | 1101221 |
| 11 | 2210212 |
| 12 | 12121201 |
| 13 | 102020102 |
| 14 | 211110211 |
| 15 | 1122221122 |
| 16 | 10022220021 |
| 17 | 20122210112 |
| 18 | 111022121001 |
| 19 | 222122012002 |
| 20 | 1222021101011 |
| 21 | 10221112202022 |
| 22 | 21220002111121 |
| 23 | 120210012000012 |
| 24 | 1011120101000101 |
| 25 | 2100010202000202 |
| 26 | 11200021111001111 |
| 27 | 100100112222002222 |
| 28 | 200201002221012221 |
| 29 | 1101102012212102212 |
| 30 | 2202211102201212201 |
| 31 | 12112122212110202102 |
| 32 | 102002022201221111211 |
| 33 | 211011122110220000122 |
| 34 | 1122100021221210001021 |
| 35 | 10021200120220120002112 |
| 36 | 20120101011211010012001 |
| 37 | 111010202100122020101002 |
| 38 | 222021111201021110202011 |
| 39 | 1221120000102112221111022 |
| 40 | 10220010000212002212222121 |
| 41 | 21210020001201012202222012 |
| 42 | 120120110010102102112221101 |
| 43 | 1011010220020211212002212202 |
| 44 | 2022021210111200201012202111 |
| 45 | 11121120121000101102102111222 |
| 46 | 100020011012000202211212000221 |
| 47 | 200110022101001112200201001212 |
| 48 | 1100220121202010002101102010201 |
| 49 | 2201211020111020011202211021102 |
x
How do the numbers of base 3 digits of vary with
?
Below are plots of the number of occurrences of digits 0, 1, 2 in the base 3 representation of for
:
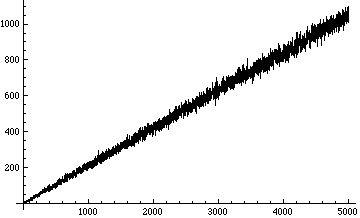
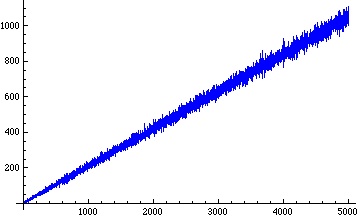
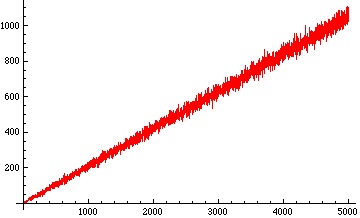
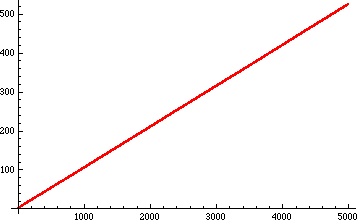
When we plot the running average of the number of occurrences of the digit 2 in the base 3 representation of – that is, the average of the numbers in the third (red) plot above from the very beginning – we get a remarkably straight line:
Erdös conjecture on the digit 2
Paul Erdös noticed that the base 3 representation of contains no 2 digit, but that after that the base 3 representation of powers of 2 seem to always contain the digit 2. He conjectured this is so, and to this day no-one knows whether this is true or not.
If we look again we see that in this list the base 3 representation of contains the digit 2 twice, and that seems to be true for the other powers
with
Put another way, seems it might be the last integer for which the base 3 representation of
contains just one occurrence of the digit 2, just as
seems to be the last integer for which the base 3 representation of
contains no occurrences of the digit 2.
We can carry out a search for those integers that are the last integer for which the base 3 representation of
contains
 or less occurrences of the digit 2.
The search reported below was restricted to .
| k | N(k) = largest n such that |
| 0 | 8 |
| 1 | 24 |
| 2 | 26 |
| 3 | 26 |
| 4 | 36 |
| 5 | 36 |
| 6 | 37 |
| 7 | 42 |
| 8 | 48 |
| 9 | 54 |
| 10 | 76 |
| 11 | 76 |
| 12 | 76 |
| 13 | 76 |
| 14 | 76 |
| 15 | 78 |
| 16 | 110 |
| 17 | 111 |
| 18 | 121 |
| 19 | 134 |
| 20 | 134 |
Note that .
This means that for all integers the base 3 representation contains more than 2, and more than 3, occurrences of the digit 2.
As we can see from the first table above, when it seems that the base 3 representation of
contains at least 4 occurrences of the digit 2. This remains true in the range
.
A plot of the estimates of is shown below:
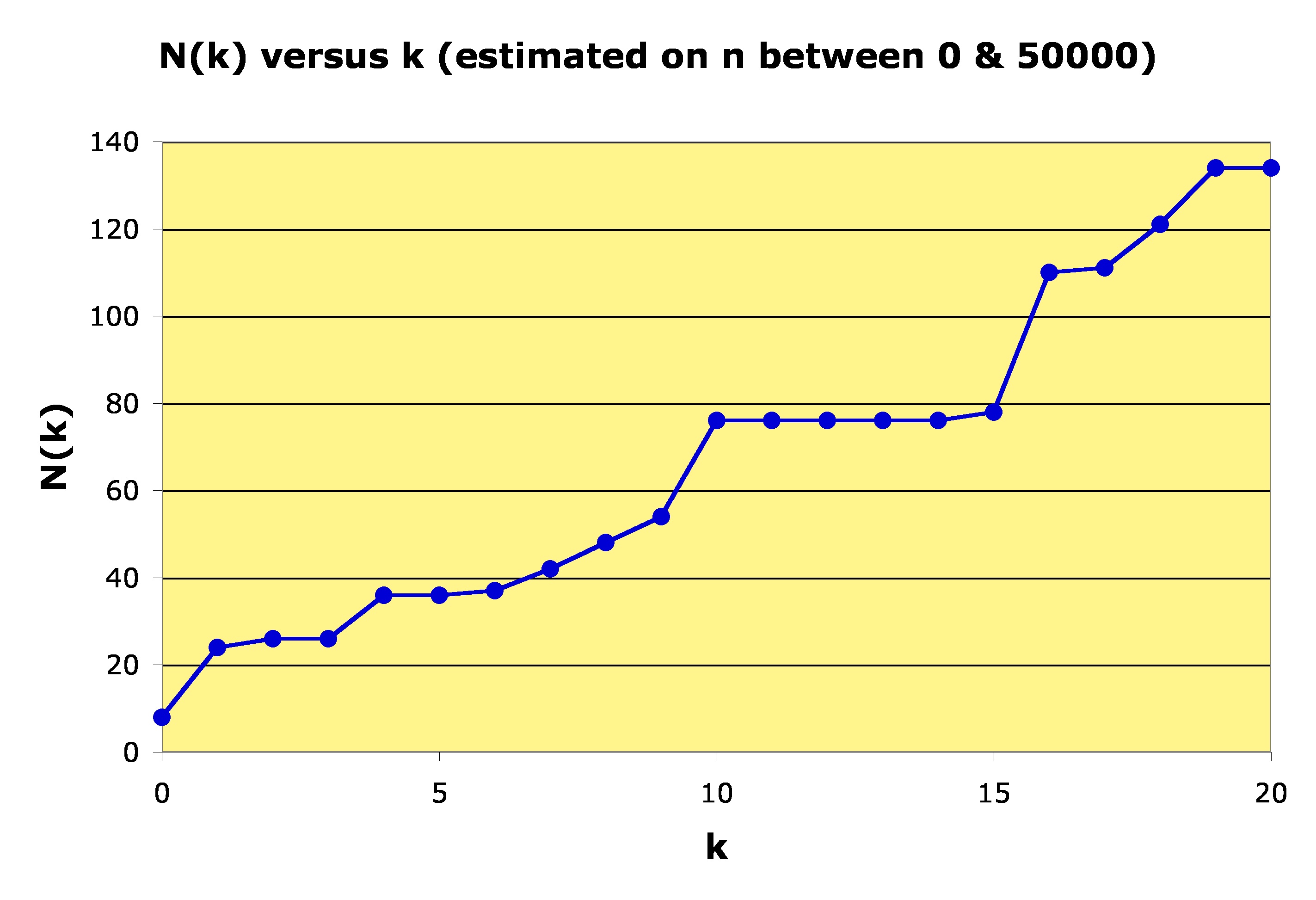 These are only estimates because we do not know for sure that further calculations for a larger range of
These are only estimates because we do not know for sure that further calculations for a larger range of might not change these values.
We do not have proofs for any of these estimates.
The occurrence and growth of the digits of in base 3 offer plenty of scope for experimentation by school students and undergraduate students of mathematics.
It seems we can obtain good guesses about the appearance of these digits, without yet knowing in any way how to prove any of these guesses.

