Some stubborn problems associated with the number 3/2
Posted by: Gary Ernest Davis on: December 4, 2010
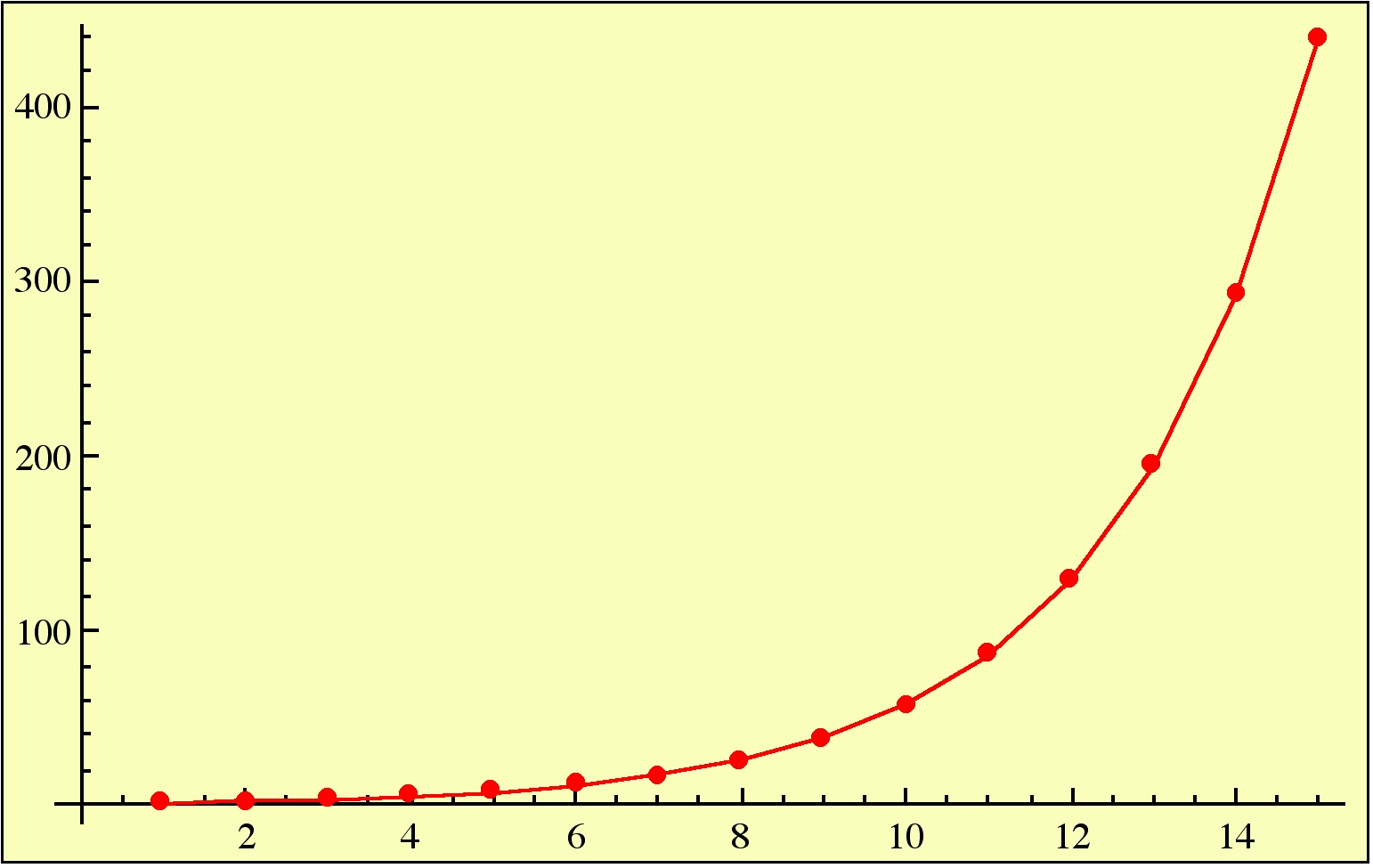
Fractional parts of powers of 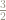
The powers of increase exponentially:
However, if we keep only the fractional part of – that is,
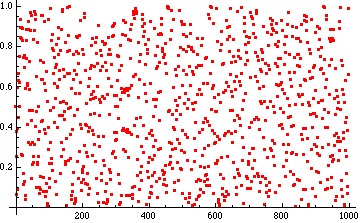
– quite a different picture results:
The first few of these numbers are 1/2, 1/4, 3/8, 1/16, 19/32, 25/64, 11/128, 161/256, 227/512, 681/1024, 1019/2048, 3057/4096.
Despite much study, there are things about this sequence of fractional numbers that are not known.
Equidistribution
If we take an interval of numbers such as and for each
count how many times
lies between
, will the ratio of the number of times to
approach the length of this interval – namely, 0.1 – as
increases?
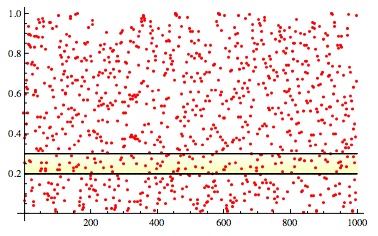
For example, in the second picture above, it is true that for exactly 101 values of we have
, and
.
This property, when true for any interval is known as equidistribution of the sequence of numbers
.
Back in 1914 Hardy & Littlewood proved that for “most” numbers the numbers
are equidistributed in the interval
.
(Hardy, G. H. and Littlewood, J. E. “Some Problems of Diophantine Approximation.” Acta Math. 37, 193-239, 1914)
It is not known if is one of those numbers.
Density
An equidistributed sequence of numbers must land in every interval
because the
must land in
the right number of times.
The property of landing in each interval at least once is called density of the sequence
.
It is not even known if the sequence is dense, let alone whether it is equidistributed.
A powerful, but stubborn, inequality
It is widely believed, but still not known, if the fractional part of , namely
, satisfies the inequality:
for all
………………..(*)
If this inequality is true then a famous problem of number theory – Waring’s problem – is known to be true.
The inequality (*) seems innocent enough, yet no-one to date has been able to prove it is true.
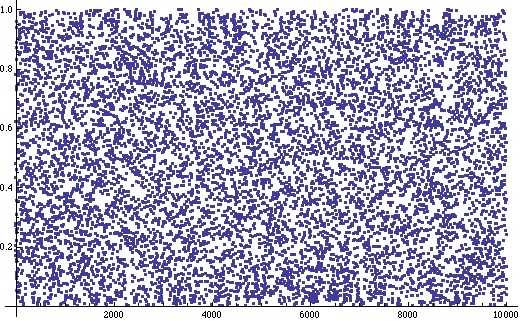
If (*) is true and we plot versus
we should never get a negative value.
A plot of the first 10,000 of these numbers looks as follows:
Of course it’s hard to see from this plot how close to 0 the values of get.
There are values of for which
is smaller than
for all previous
.
The first few of these values of and the corresponding values of
are:
| Values of n for which F(n) is less than any previous F(i) | F(n) |
| 5 | 0.168945 |
| 14 | 0.0529218 |
| 46 | 0.0317909 |
| 58 | 0.0297681 |
| 105 | 0.0144072 |
| 157 | 0.00725365 |
| 163 | 0.00449855 |
| 455 | 0.00314395 |
| 1060 | 0.00110873 |
| 1256 | 0.000564205 |
| 2677 | 0.000363945 |
| 8093 | 0.0000809868 |
| 28277 | 0.0000604566 |
| 33327 | 0.0000549506 |
| 49304 | 0.00000736405 |
x
Is this a “good” problem?
The inequality (*) is intriguing, and if you can prove it you will undoubtedly become (mathematically) famous.
But it is it a good problem to work on?
A graduate student should not work on this problem because the chances of getting anywhere new are very slim.
A professional mathematician might play with it, in the hope of having a few ideas.
School students might also play with it in the hope of getting a sense of what the problem means and why it is hard: there are very few such hard problems in mathematics, with such strong implications, that are so easily stated.
A good starting point for school students to experiment is with the the fractional part of the powers of .
Why, exactly, is the square root of 2 not a rational number?
Posted by: Gary Ernest Davis on: December 3, 2010
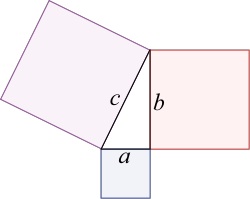
Right angled triangles and 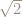
The Pythagorean theorem tells us that a square erected on the hypotenuse of a right-angled triangle will have an are equal to the sum of the areas of squares erected on the other two sides:
In particular, a right-angled triangle with the two sides adjacent to the right angle having length 1 will have a hypotenuse whose square is 2.
Pythagoras’ school of mathematics discovered that there is no ratio of whole numbers – or as we say nowadays, no rational number – whose square  is 2.
is 2.
This was shocking to the Pythagoreans because it showed that numbers, as they thought of them (whole numbers and ratios of whole numbers), could not measure all lengths. The reason this was shocking to them is that they assumed, as a matter of deep belief, that the numbers known to them could measure all known quantities.
So how can we see that is not a rational number?
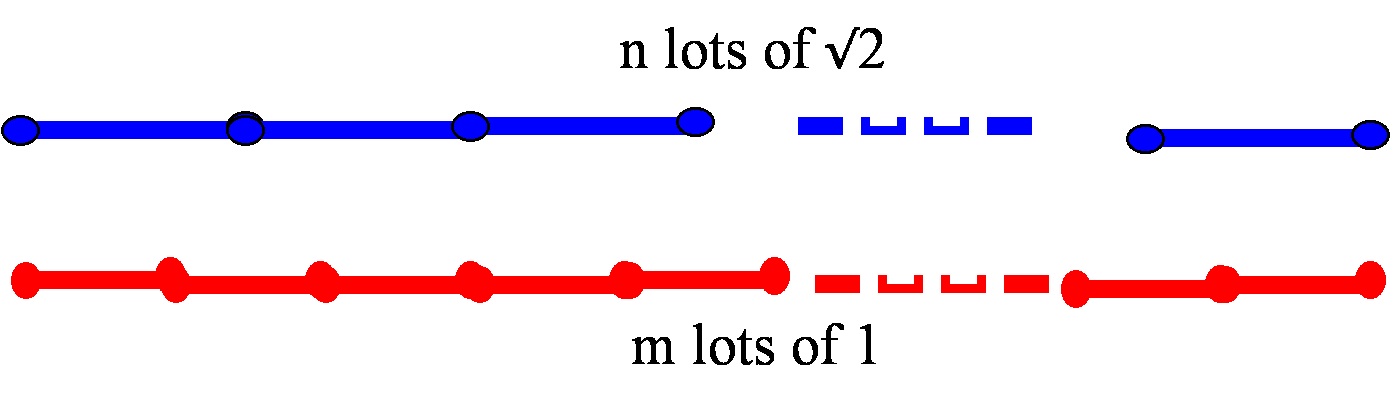
Let’s think about it the ancient Greek way: we will see that a line of length is not commensurable with a line of length 1.
By this we mean that if we step out a line of length a whole number of times the resulting length will never be the same as stepping out a line of length 1 any number of times:
How we see this is so is by stating a counterfactual situation: we enter an imaginary, potentially wholly fictitious, world in which it IS possible to exactly match a length that is a whole number multiple of with a length that is a whole number of multiples of 1:
The essence of the idea
Prior to a general argument let’s look at the basic idea in a manufactured, but illustrative, example.
Let’s imagine that .
We know this is, in fact, not quite right, because – not quite 2, but close.
Let’s just imagine, however, in a spirit of playfulness, that turned out to be exactly equal to 99.
In that case, let’s look at the number .
This number, , is a positive whole number less than 70, and we can check that:
In other words, we now have a situation where .
Now we can do this over again.
Let’s look at the number .
This new number, , is a positive whole number less than 29, and we can check that:
Now we have a situation where .
Well, you can see where we are heading; let’s do it again, with .
The number is again a positive whole number and it’s less than 29.
We can again check that is a positive whole number:
.
So now we have .
if we do this again we will get which is clearly not so.
So what? you may say. If we start with a falsehood , namely , and end up with a falsehood, namely
, what does this show?
Logically, it shows nothing, but it gives us the essence of a productive idea.
The productive idea is simply that:
if we ever have a positive whole number multiple of equal to a positive whole number then we can find smaller positive whole numbers that do the same job.
The general case
So imagine, that it is possible to match some whole number multiple of with some whole multiple of 1.
In other words, there are positive whole numbers such that
.
We will see that in this imaginary world we are lead to a contradictory state of affairs, from which we conclude that such an imaginary world does not exist.
There is a first occurrence of this phenomenon, by which we mean a smallest value of for which this happens.
Now lets look at the quantity .
First, because
. This is so because
.
Second, is a whole number because
.
Third, because
. This is so because
, since
.
Fourth,
In other words, we have found an earlier occurrence of a whole number multiple of that is a whole number multiple of 1, contrary to
being the first such occurrence.
This contradictory state of affairs means our imagined word does not exist, so a whole number multiple of can never be exactly equal to a whole number multiple of 1.
The short summary of the idea of this proof is as follows: if a positive whole number times
is a whole number, then the same is true for the smaller positive whole number
.
“Standard” proof by infinite descent
The commonly presented proof of the irrationality of is actually relatively complicated for students. When it is dissected as a structured proof one sees many subtle points in it such as knowing how and why a fraction can be written in its lowest terms (using Euclid’s algorithm). See here for more details.
Irrationality of other square roots
This is a follow up to a question from max@mathforum.
The essential point that makes the argument for the irrationality of work is that
.
Because of this fact, when we have a positive whole number n for which is also a positive whole number, then
is a positive whole number with the same property, and is less than n.
If we were to replace the number 2 by 5, for example, we would have to consider in order to get a number that is both positive and less than 1.
In general, for a non-square number p we use where
is the integer part of
.
Clearly this does not produce a positive number when p is a perfect square, so the technique breaks down then – as it should!
Cut The Knot
Alex Bogomolny has about 20 proofs that is not rational at his “Cut The Knot” site.