The axis of symmetry of a quadratic function
Posted by: Gary Ernest Davis on: November 27, 2010
Jim Tanton (@jamestanton ) Tweeted:
“x=-b/(2a) ugh!For y=3x^2-12x+7 factor first 2 terms y=3x(x-4)+7 See x=0 & x=4 give same output. Axis of symm must be x=2.Try this on y=ax^2+bx+c!”
This, in my experience, is a simple yet typical example of Jim’s thinking: highly relational and generally avoiding instrumental procedures.
In this post I simply want to elaborate on this idea.
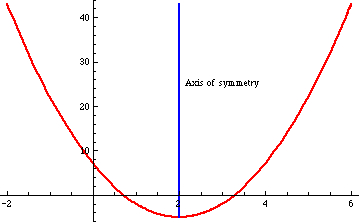
A quadratic polynomial function is symmetric about some line
. Also,
is either entirely increasing, or entirely decreasing, to the left of the line of symmetry, and to the right of the line of symmetry it is doing the opposite:
Students are often – usually? – taught that the axis of symmetry is without any rhyme or reason.
Knowing this is “knowledge that” something is so, without any relational understanding of why: students can “know that” without “knowing why”. Richard Skemp elaborated on the differences between relational and instrumental understanding, and his article is worth reading (again) in this context.
Let’s look in more detail at Jim Tanton’s example, above.
The quadratic polynomial can be written as
. This simply results from the common factor of “
” in
and
.
We can make the term equal to 0 in two ways: by making
and by making
.
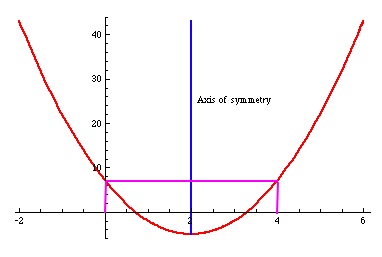
For both these values, , we have
.
In other words, at the function
takes the same value (namely, 7).
Because is symmetric about some line
, and decreasing/increasing differently on opposite sides of the line of symmetry, this axis of symmetry occurs midway between
, that is, at
:
Let’s take another example: the quadratic polynomial .
Using Jim Tanton’s idea we factor from the first two terms to get
.
From this we see, as before, that .
Again, because the quadratic polynomial is symmetric about a vertical line and decreasing/increasing differently each side of that line, the line of symmetry is .
Applying this idea to a general polynomial , where
we see that
so the axis of symmetry is midway between
, that is at
Instrumental “understanding” involves being able to follow a set of instructions without knowing why you are doing so.
Relational understanding involves understanding the relationship of one thing to another to help guide you to a correct conclusion.
As Richard Skemp points out, relational understanding sometimes takes a little more mental effort to get what is going on, but pays off in terms of both flexibility, and a feeling of genuine understanding, stemming from seeing the relationship between various things.
Should students memorize the quadratic formula?
Posted by: Gary Ernest Davis on: November 26, 2010
 Recently, Dan Meyer @ddmeyer Tweeted:
Recently, Dan Meyer @ddmeyer Tweeted:
x
x
x
The quadratic formula
Rote memorization
This is about a useless a technique as was ever thought of for educational purposes, yet it is trotted out often by teachers: “Why won’t they just rote memorize it?”
What this concern betrays, in my experience, is a lack of understanding of human memory systems – the aspect of brain functioning that is critical to education.
The definitive study on rote memorization was done by Hermann Ebbinghaus and published in 1885. He studied the rate of learning and forgetting of nonsense syllables by himself, and formulated his law of forgetting in which an exponential decay describes the rate at which rote memorized information is lost.
One might argue that mathematical terminology, facts, procedures, and formulas are not nonsense syllables, having a great deal of logical structure.
This argument misses the point that to many students the mathematics they are expected to remember appears to them to be more or less nonsense syllables, devoid of any real meaning.
Mathematical experience is not, for these students, something that they can fit into a broader scheme of related memories.
As a result their knowledge decays exponentially and, as experience shows, with a quite small half-life.
Rote memorization decays exponentially and we can only safely rely on recall of something rote-memorized if it is continually practiced and refreshed.
Permastore memory
Harry Bahrick studies very long term memory.
Here’s what he had to say about long term memory and education in the Oxford Handbook of Memory:
“Educators have emphasized the immediate achievements of students, paying little attention to the effects of their instruction on long-term retention of content.”
His research has unearthed a number of important issues:
- Instructional techniques that favor rapid learning may yield poor retention.
- Spaced rehearsals can dramatically enhance accessibility of even marginal content for long periods of time.
- Content that is not frequently accessed (e.g. mathematics) could remain accessible by implementing brief appropriately spaced retrieval practice sessions.
The major lessons for mathematics teachers that result from Bahrick’s research are that focusing on rapid achievement is likely to inhibit longer term retention. Practicing recall of earlier learned material at spaced intervals can dramatically increase longer term recall.
Schema
Theory of quadratic equations
How “should” a student solve quadratic equations?
- Divide by the coefficient of
. This gives us the equation
- Move the constant term to the other side of the equation:
- Add as much to both sides of the equation as is needed to make the left side a perfect square:
- Re-write the equation as a perfect square equals a constant:
- Recognize there are solutions if the right side of this equation is not negative:
- Take square roots:
(remembering that a number and its negative square to the same result)
- Rearrange to find the solutions:
- Make things a little simpler if possible:
Postscript
- We multiply through by
to get
- Recognize this as
- Rewrite as
- Take square roots to get
- Rearrange to get
- Simplify if possible: