Ore numbers: how do they grow?
Posted by: Gary Ernest Davis on: November 15, 2010
An Ore number (also known as a harmonic divisor number) is a number whose harmonic mean of its divisors is an integer.
The harmonic mean of a set of numbers is
.
When the are the whole number divisors of the number n, then we get the harmonic mean of the divisors of n.
These numbers were named for Øystein Ore who proved that all perfect numbers are Ore numbers. Recall a whole number is perfect if the sum of the divisors of the number is exactly twice the number. 6 and 28 are well-known perfect numbers.
For example, the divisors of 3 are 1 and 3, so the harmonic mean of these divisors is which is not an integer, so 3 is not an Ore number.
More generally, if is a prime number then the harmonic mean of its divisors is
which is not an integer, so no prime number is an Ore number.
On the other hand, the divisors of 6 are 1, 2, 3 and 6 so the harmonic mean of these divisors is so 6 is an Ore number.
Using a computational language such as Maple, Mathematica, MATLAB or Python one can calculate a few Ore numbers.
Here is a list of the Ore numbers up to 10,000,000:
1, 6, 28, 140, 270, 496, 672, 1638, 2970, 6200, 8128, 8190, 18600, 18620, 27846, 30240, 32760, 55860, 105664, 117800, 167400, 173600, 237510, 242060, 332640, 360360, 539400, 695520, 726180, 753480, 950976, 1089270, 1421280, 1539720, 2178540, 2229500, 2290260, 2457000, 2845800, 4358600, 4713984, 4754880.
How fast do these Ore numbers grow?
Let’s write for the
Ore number.
So, and so on.
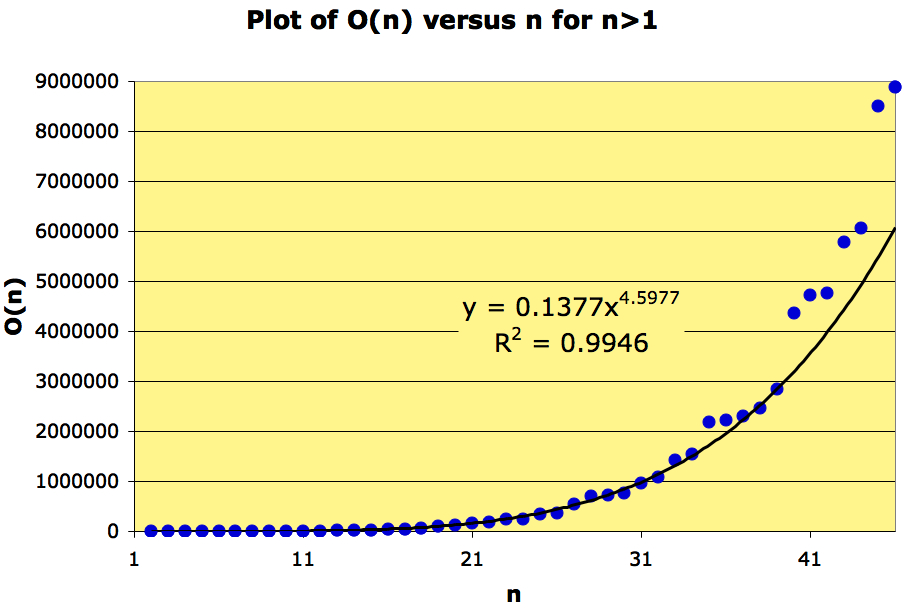
What does a plot of versus
look like?
A regression indicates that grows as a power of n, at least in the range
A plot of should therefore look like a straight line, and it does:
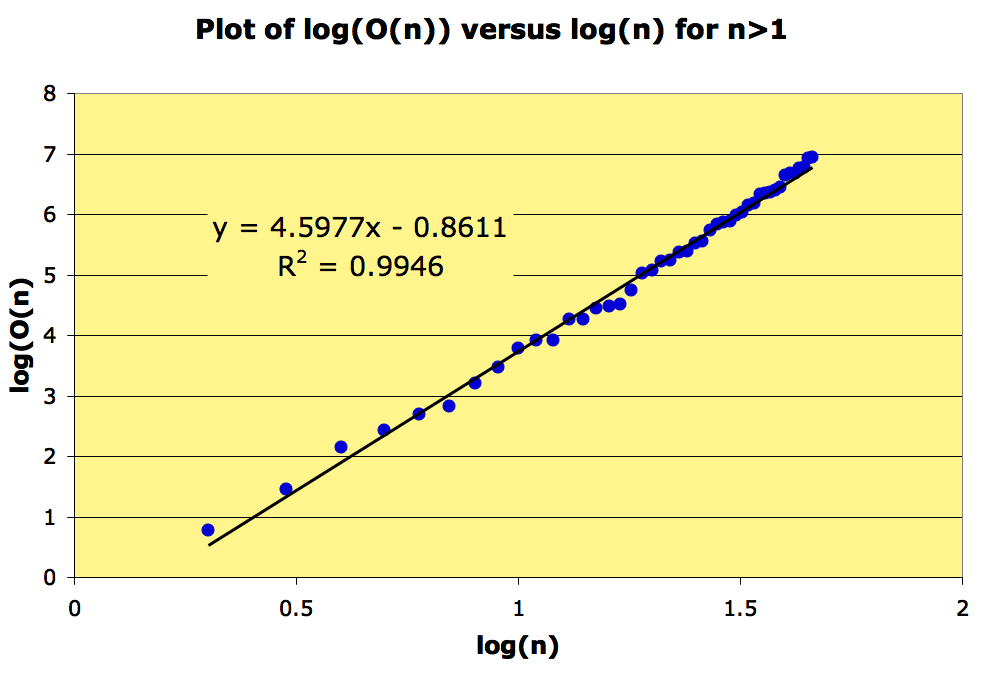 This suggest that there are constant
This suggest that there are constant such that as n increases,
.
If this is so, then .
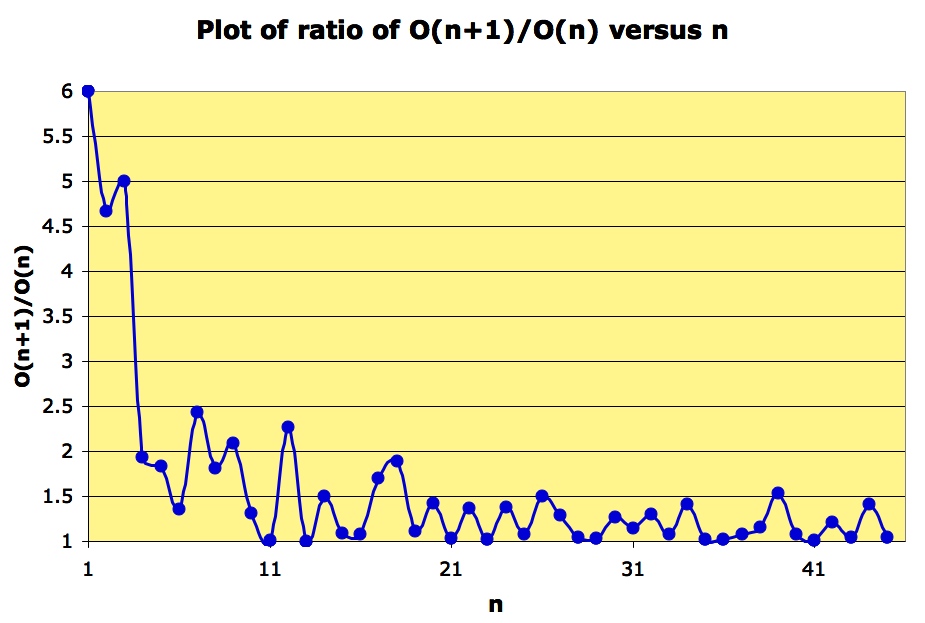
From the data we have for the Ore numbers less than 10000000 the plot of looks as follows:
So, does ?
This is a weaker question than: “is for some constants
“.
Postscript
- There is a Facebook page for Ore numbers.
- Here are the Ore numbers up to 1 billion ( = 1,000 million):
1, 6, 28, 140, 270, 496, 672, 1638, 2970, 6200, 8128, 8190, 18600, 18620, 27846, 30240, 32760, 55860, 105664, 117800, 167400, 173600, 237510, 242060, 332640, 360360, 539400, 695520, 726180, 753480, 950976, 1089270, 1421280, 1539720, 2178540, 2229500, 2290260, 2457000, 2845800, 4358600, 4713984, 4754880, 5772200, 6051500, 8506400, 8872200, 11981970, 14303520, 15495480, 16166592, 17428320, 18154500, 23088800, 23569920, 23963940, 27027000, 29410290, 32997888, 33550336, 37035180, 44660070, 45532800, 46683000, 50401728, 52141320, 56511000, 69266400, 71253000, 75038600, 80832960, 81695250, 90409410, 108421632, 110583200, 115048440, 115462620, 137891520, 142990848, 144963000, 163390500, 164989440, 191711520, 221557248, 233103780, 255428096, 287425800, 300154400, 301953024, 318177800, 318729600, 326781000, 400851360, 407386980, 423184320, 428972544, 447828480, 459818240, 481572000, 499974930, 500860800, 513513000, 526480500, 540277920, 559903400, 623397600, 644271264, 675347400, 714954240, 758951424, 766284288, 819131040, 825120800, 886402440, 900463200, 995248800
Turning a heel: can knitting contribute to mathematics education?
Posted by: Gary Ernest Davis on: November 14, 2010
 Turning a heel when knitting a sock is a big deal for beginning knitters.
Turning a heel when knitting a sock is a big deal for beginning knitters.
The Yarn Harlot (Steph Pearl-McPhee: @YarnHarlot) writes in her book “Knitting Rules!“, that:
“Turning the heel is a mythic act, one that sock knitters speak of with reverence. Turning the heel is when you, through an incredibly simple but clever series of short rows …Â make the sock change direction and move from leg to foot. I’ve done a hundred socks and I feel smart every time.”
Knitting is an intellectual activity: knitters have to think, solve problems, count, and think some more. Yet it is an activity with a physical product: in the case of turning the heel, the product is a sock, or two.
x
From the Yarn Harlot’s words I feel that turning a heel in knitting is a metaphor for many of life’s successful problem solving attempts:Â turning the heel is a mythic act, one spoken of with reverence, and one feels smart every time one does it.
Knitting is a very democratic activity. As the Yarn Harlot writes in “Knitting Rules!: “there are no knitting police.”
Knitting is also something that people of all ages -Â very young to very old – can do.
Mathematics is full of problems, and problems solving is a major part of mathematical activity. One might argue that all professional mathematicians do is solve problems. Mathematics also has no math police, and people of all ages can successfully do mathematics.
Yet mathematics does not, in general have such physical products as socks, or sweaters.
Generally mathematics is more about analysis, using calculation and reasoning.
So, my question is: “Is there a mathematical activity that corresponds to turning the heel in knitting?”
My colleague Sigal Gottlieb says that for her the mathematical activity that might be close to turning the heel in mathematics is finding the formula for the volume of a sphere by integration.
So, dear reader, is there a mathematical activity that for you corresponds to turning the heel? Or is it just that mathematics consists of a series of intellectual and emotional highs that come from successful problem solving, and that there is no one thing that might correspond to turning the heel?