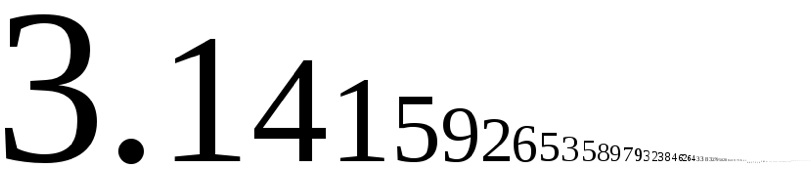What does it mean to know a number? Pi for elementary teachers
Posted by: Gary Ernest Davis on: November 12, 2010
Area and “amount of stuff”
The area of a region is often colloquially thought of as the “amount of stuff” in that region.
This is not a good way of thinking about area because it leads to odd thinking such as the area of a region does not change if the perimeter changes “because the amount of stuff” hasn’t changed – as if the boundary of the region contains “stuff” that is conserved as the shape of the boundary changes.
There is obviously something wrong with this “amount of stuff” model because a square of side lengths 1 cm has the same perimeter – 4 cm -Â as a rectangle with side lengths 
Square and rectangle have the same perimeter. Each small square has area 1/4 square cm
So, the “amount of stuff” model of what’s inside a boundary leads to silly situations.
Conclusion? There is no “stuff” inside a boundary in the plane – that is, inside a closed non-intersecting figure drawn on a sheet of paper:
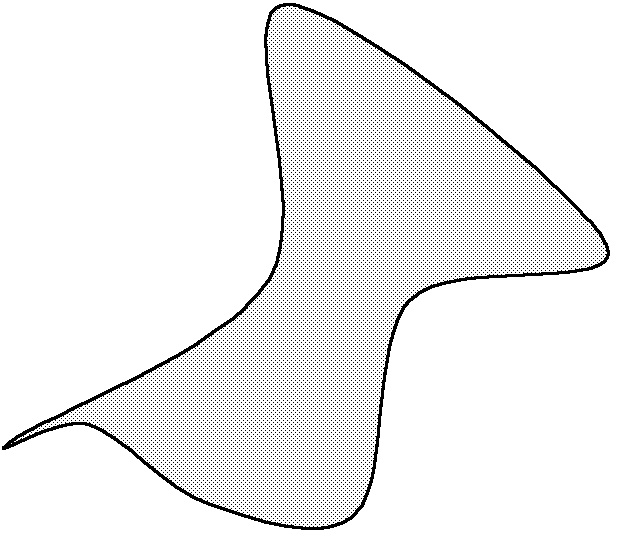
Contrary to appearances, there is no "stuff" inside this closed figure that is conserved as the shape of the boundary changes.
The area of a region therefore has nothing to do with any hypothetical “stuff” surrounded by the boundary of the region.
What then is the area of a region?
Part of the answer goes back to activities that teachers get children to do in the earliest grades – counting squares.
Many years ago when I was sitting in on a grade 2 class the teacher had the students draw objects on a gird of squares and asked them to count squares to estimate the area of the object they drew. I drew a robot that consisted of either rectangles of triangles (which are half rectangles). I did this because it would be easier to count squares if there weren’t any curvy bits to my figure. The children went “Ooh!’ when they saw my drawing, and of course, made me feel very clever!
This is a correct way of thinking about area: the number of unit sized tiles that it takes to exactly cover the figure, with no ties overlapping. For the children the grid squares were the unit tiles.
This way of thinking about area is a cognitive root: it is not the whole story about area, but it is easy for children to understand and does not have to be ditched when we learn more sophisticated notions of area.
Area of a circle
Some years ago, sitting with my friend and colleague Neil Pateman and a group of prospective teachers, in the sunshine at the University of Hawai’i at Manoa, one of the students said: “That’s what I don’t get. How do you measure a round circle in square inches?”
She was referring to the measurement of the area of a region bounded by a circle:
How many square tiles cover the circular region?
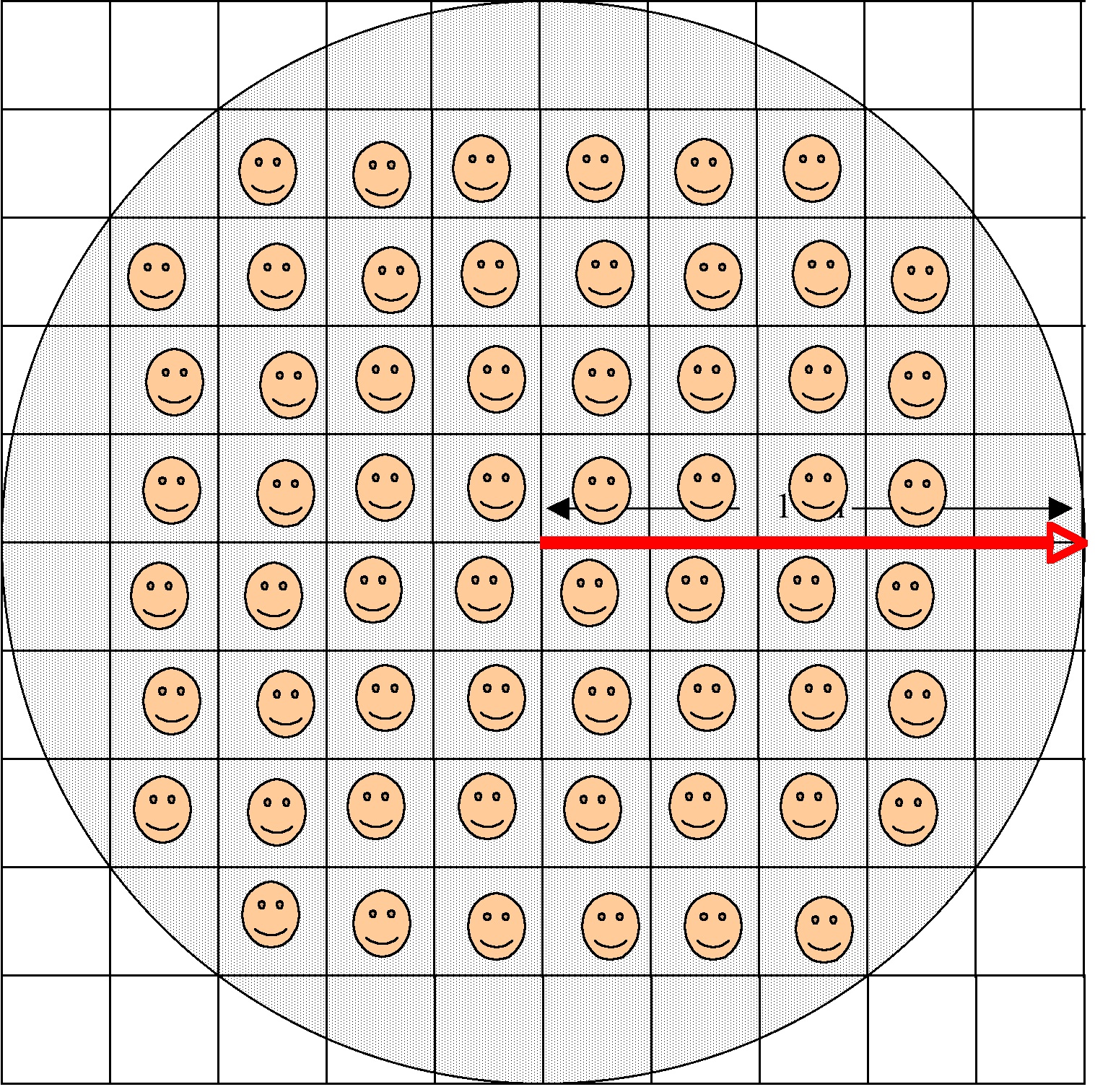
We can see that the question “How many square tiles cover the circular region?” does not have an exact whole number answer for the grid we have drawn.
It does not even seem to have an obvious fractional answer, due to the curvature of the circle as it passes over the grid lines.
Can we make an estimate of how many small tiles cover the circular region?
There are 60 small squares – those with smiley faces – that fit inside the circular region.
There are some other small squares – 28 of them – that contain either large or small pieces of the circular region.
So we know that 60 small squares lie inside the circular region, and 28 others overlap. Let’s estimate, roughly, that half of each these 28 other squares lies inside the circular region. This gives us an estimate of 60+28=88 small squares that either lie inside, or overlap by about half, the circular region.
What’s the area of these 88 small squares that lies inside the circular region?
With the radius of the circle shown as 1 cm, each small square has side length 
60 of these small squares lying inside, and 28 lying about halfway inside, the circular region gives us an area of 
This answer is not exact, because we made rough estimates.
Another way to estimate the area of the circular region would be to take the average of the area of the small squares lying inside it and the area of the large square containing it. This average is 
To get better estimates we could take a finer grid.
What is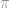 
?
Because we can take finer and finer girds to estimate the area of a circular region it seems reasonable to assert that the circular region actually has an area. In 1706, William Jones introduced a name,
This just a name, yet we have estimated that, roughly, 
What then is really the value of
How might we try to answer this question?
One way would be to try to write 
Unfortunately, this is not possible:
This is not unlike 
Yet 
Can we write
Much effort has gone into this question.
As of September 26, 2010, Alexander J. Yee & Shigeru Kondo had calculated 5 trillion digits of
The fact is that we do not know, and never will know the exact numerical value of
We know a lot of other things about
Adding structure to solve a problem
Posted by: Gary Ernest Davis on: November 9, 2010
James Tanton (@jamestanton) tweeted the following problem:
“25 people stand in a 5×5 grid of squares,1 per cell. At blow of whistle each is to take one step L, R ,U or D to a new cell, 1 per cell. How?”
The problem does not state the grid is in a plane, but if, for example, it were on a cylinder or a torus then everyone could just move left, so that would easily solve the problem.
Let’s look at a possibly easier version of the problem using a 3 x 3 gird:
| A | B | C | |
| 1 | |||
| 2 | |||
| 3 |
Here the columns are labeled A, B, C and the rows labeled 1, 2, 3.
The person at B2 has to move somewhere – so let’s assume that person moves to B1; the other cases will be dealt with in an exactly similar way. Now the person at B1 has to move either to A1 or to C1. Let’s assume it’s to A1: the other case is dealt with similarly.
Now the person at A1 can only move to A2. What about the person at C1? That person can only move to C2. But someone has to move to C1, and the only person who can now do that is at C2, so C1 and C2 swap places. Now the person at C3 has to move to B3, and there is no-one who can move to C3, since C2 has already moved to C1.
In other words, on a 3 x 3 grid, it is not possible to move the 9 people up, down, left or right, so that each moves to a new square, occupied by only 1 person.
This reasoning applied to a 5 x 5 grid would lead to many more possibilities.
When we get into this situation of having to consider many branching possibilities, one trick to help us is to put some extra structure on the problem. This extra structure cannot change the problem statement, but can add a dimension, such as color, that allows us to see more clearly what can and cannot happen.
So let’s color a 5 x 5 grid as follows:
Every person is on either a red or a yellow square.
When a person moves they move to a square of a different color.
There are 13 red squares.
Each of the 13 people on these red squares will move to a yellow square.
But there are only 12 yellow squares.
So 2 people on a red square before the whistle blows will have to occupy the same yellow square after they move.
So the proposed move is not possible.
This is an example of Dirichlet’s pigeon hole principle.
The added coloration – not originally part of the problem – allows us to see finer detail through the colored lens, and allows us to solve the problem relatively easily.
A lot of mathematical problem solving is like this: finding extra structure that adds fine detail, so allowing us to more easily solve a problem.
Now that we can see what happens when we color the 5 x 5 grid we can also see that the number 5 is not important; what is important is that 5 is odd. So the same conclusion would apply to a (2n+1) x (2n+1) grid.
Of course on an even grid – a 2n x 2n grid – we can move in 2 x2 , 4 x 4, 6 x 6 … circles, so it IS possible for the people to move on a 2n x 2n grid.
Postscript
James Tanton shows another use of Dirichlet’s pigeon-hole principle to show that some power of 3 must end in the digits 01.
He also gives an answer to his own problem analyzed in this post.
