Republic of Mathematics blog

The moving pointer and 0.999…. A useful cognitive root

Posted by: Gary Ernest Davis on: November 1, 2010

In: Uncategorized
7 Comments

Debates arise periodically as to whether 0.999… is equal to 1.Â Here, the the 9’s never end in the expression “0.999…” .

To paraphrase at least one U.S. President, the answer depends on what we mean by “equal”.

Equality

Equality takes some explaining in a mathematical setting.

As an example that is familiar to almost everyone, the fractions $\frac{1}{2}$ and $\frac{500}{1000}$ are commonly regarded as equal and we write $\frac{1}{2}=\frac{500}{1000}$ .

Yet $\frac{1}{2}$ is not identical with $\frac{500}{1000}$ . There are least two ways in which this is so. First, we do not see a $500\textrm{ or } 1000$ in the fraction $\frac{1}{2}$ . The form of these two fractions is different. Secondly, 1 part of an object – such as a cupcake – that has been divided into 2 equal pieces is quite different from 500 pieces of a cupcake that has been divided into 1000 equal pieces.

So what do we mean when we say that $\frac{1}{2}$ and $\frac{500}{1000}$ are equal?

We mean that $1\times 1000=2\times 500$ .

More generally, two fractions $\frac{a}{b}, \frac{c}{d}$ are equal when $a\times d = b\times c$ . Here, we take it for granted that we know what we mean by equality of whole numbers.

Decimals

Fractions can be written as – possibly infinite – decimal strings using the digits $0, 1, \ldots 9$ .

The basic idea of a decimal string $x=0.a_1a_2a_3\ldots$ is that multiplication by 10 moves the digits to the left: $10\times x = a_1+0.a_2a_3a_4\ldots$ . The reason for this is that we are thinking – in the back of our minds – that $x=0.a_1a_2a_3\ldots$ should mean $\frac{a_1}{10}+\frac{a_2}{100}+\frac{a_3}{1000}+\ldots$ , whatever a possibly infinite sum might mean.

We avoid thinking about infinite sums by just focusing on the decimal strings themselves.

How could we write a fraction such as $\frac{1}{3}$ as a decimal string: $\frac{1}{3}=0.a_1a_2a_3\ldots$ ?

Using the basic property of decimal strings, described above, we would have $10\times\frac{1}{3}=a_0+0.a_2a_3a_4\ldots$ . But $10\times\frac{1}{3} = 3+\frac{1}{3}$ so we would have $a_1=3 \textrm{ and } 0.a_2a_3a_4\ldots =\frac{1}{3}$ . Now we are right back where we started, so we will have $a_n=3\textrm{ for all } n$ .

In other words, using the basic property of decimal strings that multiplication by 10 moves the digits to the left, we have theÂ decimal representation $\frac{1}{3}=0.333\ldots$ . Here the “3”s go on forever, without end.

This is a cute trick, but what could it mean? We cannot resort to infinite sums if we do not know what real numbers are, so we need another interpretation to guide our intuition. This is not so much a matter of mathematical logic, which is well-covered by any number of ways of constructing the real numbers, as it is of an intuitive understanding of equality of real numbers, represented as decimal strings. Our aim is to increase, not decrease, understanding for students and teachers.

A decimal string as a sequence of instructions

Let’s think about a decimal string $0.a_1a_2a_3\ldots$ as a sequence of instructions: each of the digits $a_n$ is instructing us to move a pointer to a certain place on a line. We will use the decimal representation $0.333\ldots \textrm{ for } \frac{1}{3}$ to illustrate what we mean by a sequence of instructions for moving a pointer on a line.

Imagine a pointer pointing at 0 on the number line:

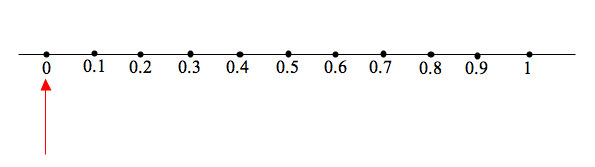Here the decimal strings $0.1, 0.2, \ldots 0.9$ have been placed on the line at spots that divide the numbers between 0 and 1 into 10 equal-sized intervals. These decimal strings represent the numbers $\frac{1}{10},\frac{2}{10}, \ldots , \frac{9}{10}$ .

The first digit – namely 3 – in the decimal string for $\frac{1}{3}$ indicates that we should move the pointer somewhere between the $0.3 \textrm{ and} 0.4$ spots:

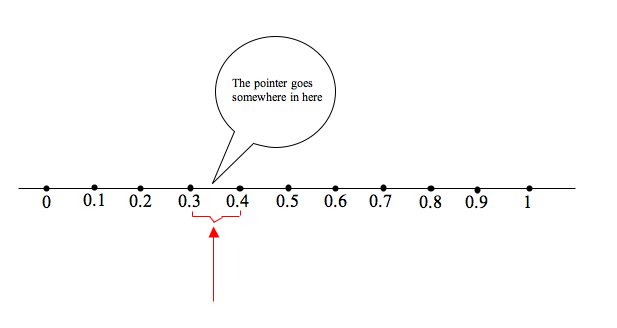To figure out where between 0.3 and 0.4 the pointer goes, we divide the space between 0.3 and 0.4 into 10 equal size intervals. We label the new endpoints of these intervals $0.31, 0.32, 0.33, 0.34, 0.35, 0.36, 0.37, 0.38, 0.39$ .

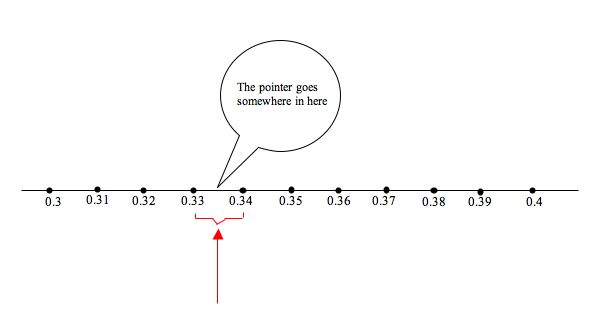The second digit – namely 3, again – in the decimal string for $\frac{1}{3}$ indicates that we should move the pointer somewhere between the $0.33 \textrm{ and} 0.34$ spots, as in the diagram.

Again, this does not pin down the pointer exactly. So we take the interval between 0.33 and 0.34 and divide it into 10 equal sized intervals. The new labels for the endpoints of these intervals will be $0.331, 0.332, 0.333, 0.334, 0.335, 0.336, 0.337, 0.338, 0.339$ .

We read the thirdÂ digit-Â 3, again – in the decimal string for $\frac{1}{3}$ and move the pointer somewhere between the $0.333 \textrm{ and} 0.334$ spots.

This process of moving the pointer will never end, because there is a never ending sequence of 3’s in the decimal string for $\frac{1}{3}$ . The pointer never stops: it never actually points at $\frac{1}{3}$ at any stage we move it.

In terms of the moving pointer, how can we interpret $\frac{1}{3}=0.333\ldots$ ?

One way to answer this question is to say that as we move the pointer according to the instructions encoded in the decimal string $0.333\ldots$ , the distance between the pointer and $\frac{1}{3}$ becomes progressively closer to 0.

If we had placed the pointer at the left hand end of an interval at each step, the distance between the pointer and $\frac{1}{3}$ would reduce by $\frac{1}{10}^{th}$ each time.

That it is one way to think about the “=” in $\frac{1}{3}=0.333\ldots$ .

This is what is known as a “cognitive root” in the learning and teaching of mathematics:

It is an idea that is based on something relatively easy to grasp.
It is not the whole story – more sophisticated mathematical thought adds to, and enriches the idea.
The idea is not thrown away as a student encounters more sophisticated mathematics: it is simply built upon.

The same idea of “equals” applies to $0.999\ldots = 1$ .

We imagine a pointer located at 0 and move it to 0.9. The distance between the pointer and 1 is $\frac{1}{10}$ .

We take the next digit in the decimal string – 9 – and move the pointer to 0.99. The distance between the pointer and 1 is now $\frac{1}{100}$ . Each time we move the pointer according to the instruction encoded in the next digit in the decimal string the distance between the pointer and 1 is reduced by $\frac{1}{10}^{th}$ .

That is the sense in which we mean “=” in $0.999 \ldots = 1$ .

It all depends,Â to paraphrase a former US President again, what we mean by “equals.”

For a related discussion, see James Tanton’s video “Point Nine Forever”:

James rightly points out, in different terminology,Â that if the decimal string $x = 0.999\ldots$ is to represent a number at all, then, by our fundamental operation of multiplying the decimal string by 10 we have $10\times x = 9+0.999\ldots = 9+x \textrm{ so } 9\times x = 9 \textrm { and therefore } x=1$

Vertical integration of mathematics K-20

Posted by: Gary Ernest Davis on: October 28, 2010

In: Uncategorized
2 Comments

The @mathchat topic for Thursday October 28, sale 2010 is: “How can we facilitate vertical (cross-curricular) integration of mathematics teaching from early years to graduate-level?”

In this post I want to think about the vertical integration aspect of this question.

Below are some issues that I feel need to be addressed in a genuinely productive and transformative mathematics curriculum K-20.

Number-sense – a strong understanding of numerical operations – does not stop in elementary school. Number sense needs to be re-visited, there in increasingly deeper ways, help K-20.
Geometry – particularly the visual aspect of geometry, – needs to be integrated with algebra from the very beginnings of algebra. This is especially so for “Early Algebra”. Visual processing and syntactic processing seem to be different brain activities – integrating them would seem to lead to deeper mathematical understandings, and longer lasting memories.
Computation and computational devices need a coherent K-20 focus. Computation is not just about getting an answer but knowing how to reason that the answer is correct. Computation involves necessary approximations ( $frac{1}{3}approx 0.333$ ); machines make approximation errors; errors propagate; analyzing errors is critical.
Trigonometric functions are circular functions, not triangular functions. Focusing on the unit circle from the beginning of trigonometry paves the way for deeper understanding of, and facility in, calculus.
Statistics runs through everything: analysis of data is basic to all mathematical activity. Going back to statistical basics – mean, mode, variance, skewness, is critical every time data – from records, experiments, or situations – is analyzed.
Algorithmic thinking is basic to mathematics. Applying an algorithm, understandingÂ it, analyzing it, finding its run time are progressively deeper engagements with basic algorithmic thinking.
Thinking in terms of functions, from the early years. The organizing idea of a function is foundational to modern mathematics: it needs to take precedence over formulas.
Inquiry driven mathematical investigations.
Extended project work at least as often as repetitive homework.
Learning lessons from, and at, all levels. Teachers of mathematics should see themselves as part of a community that includes K teachers as well as graduate advisers. Research mathematicians and university professors need to take issues of teaching and learning in the early grades seriously. Equally, elementary and secondary teachers need to learn about mathematical topics out of their comfort zone, and learn about research problems. We are all learners in one way or another. We should emphasize our common interest rather than divisions.
Above all, teachers of mathematics at all levels should see mathematics as a very cool, very empowering subject, that can raise young minds to new heights.

Math is a critical part of the education of all people. We can write math worksheets, offer math homework help, design math games – even cool math games, find math tutors, and set challenging math problems. But until we come together as a K-20 math community to discuss our understandings of mathematics, to voice our concerns about teaching, we will not begin to tackle the fragmented and piecemeal nature of mathematics teaching and learning.

Tags: integration, math, math homework, math worksheets

Republic of Mathematics blog

The moving pointer and 0.999…. A useful cognitive root

Equality

Decimals

A decimal string as a sequence of instructions

Vertical integration of mathematics K-20

Math Blogging

Great mathematics sites

Visitor map