Probabilities: when do we add and when do we multiply?
Posted by: Gary Ernest Davis on: October 27, 2010
 @davidwees asked on Twitter: “Looking for ideas so students can experiment with the difference between mutually exclusive & independent events in probability.”
@davidwees asked on Twitter: “Looking for ideas so students can experiment with the difference between mutually exclusive & independent events in probability.”
My Twitter response was: “May sound strange, but: when do probs add, when do they multiply? Explore.”
In this post I want to think about mutually exclusive and independent events from a teaching point of view.
One issue, as I Tweeted to @davidwees is that we have a definition of mutually exclusive other than probabilities add, but we have no definition of independent other than probabilities multiply (or something immediately equivalent: see the postscript, below).
So let’s look at a simple example where students might explore addition and multiplication of probabilities.
Tossing a coin and rolling a die
This example involves tossing a fair coin and rolling a fair die.
The elementary events are pairs where
and where
.
We can lay out these elementary events in a table, as follows:
|
(H, 1) |
(H, 2) |
(H, 3) | (H, 4) |
(H, 5) |
(H, 6) |
|
(T, 1) |
(T, 2) |
(T, 3) |
(T, 4) |
(T, 5) |
(T, 6) |
There are 12 elementary events and so compound events in total.
Let’s take the event A, consisting of pairs where the die rolls an even number, and the event B where the die rolls an odd number.
So we have:
and
Is ?
Yes, because .
Is ?
No, because .
Here are 2 events, both of size 4, chosen at random from the elementary events:
and
Is ?
No, because .
These events were chosen randomly using the folowing Excel commands:
| =IF(RAND()<1/2,”H”,”T”) | =INT(RAND()*6)+1 |
| =IF(RAND()<1/2,”H”,”T”) | =INT(RAND()*6)+1 |
| =IF(RAND()<1/2,”H”,”T”) | =INT(RAND()*6)+1 |
| =IF(RAND()<1/2,”H”,”T”) | =INT(RAND()*6)+1 |
x
When do probabilities add?
The answer of for
is just
short of
.
That comes from the elementary event
being in both
but only once in
.
This situation is typical: any time have elementary events in common, those elementary events will only be counted once in
but will be in both
. In this situation we will have
.
On the other hand, if then the number of – equally likely – events in
is just the sum of the number of lelmentary events in
and the number of elementary events in
.
So, at least for the example above, exactly when
.
When do probabilities multiply?
When might we have ?
In the situation of our example, .
So:
while
.
and we have exactly when:
An example would be when and
For example: .
There are many other pairs of events
Student exploration
Because “independence” is a name given to events it seems pedagogically sensible to first encourage students to explore, in simple examples like that above, how it might happen that
.
When students have many examples of this phenomenon, it then – and only then – makes sense to give it a name: “independence”.
To first define “independence” in terms of is to enter the realm of advanced mathematical thinking – a realm where examples conform to abstract definitions, and properties are logical deductions from the definitions. Beginning students need to see definitions as organizing names for an idea, that “begs to be organized” from many examples.
Postscript
Many Tweeps, and some commentators, have opined that the basic way of expressing independence is .
This is fine if one knows what is .
An answer such as “The probability that A happens given that you know B has happened” is not very helpful in actually calculating probabilities.
For that one needs a more precise definition and the usual one is .
One can then define independence by but that is exactly equivalent to
.
Conditional probabilities are, in my experience, quite difficult for students of all ages to get their heads around.
If someone can suggest a series of explorations that assist high school students to become comfortable working with conditional probability then that would, of course, be another route to independent events.
If you have such explorations, or know of them, I would be very glad to hear of them, as would the mathematics teachers whose questions prompted this post.
Sharing such knowledge about the learning and teaching of mathematics is what the Republic of Mathematics is all about.
An example that illustrates – to me at least – how thorny are both conditional probability and independence for students comes from geometric probability.
Suppose we consider measurable subsets of a unit square – sets that have a well-defined area.
Define a probability measure on such sets by area: .
Now consider the following two sets .
Then so
are independent.
Is this any more or less intuitive than ?
How much does that glass of wine cost?
Posted by: Gary Ernest Davis on: October 27, 2010
No: the answer depends on how old you are when you drink it, and what you would do with the money otherwise.
I was watching a recent Suze Orman show and I admired the way she drove home the real cost of spending by relating it to a single everyday item.
Here’s my take on her message.
Suppose a young person spends 0 each month on entertainment which amounts mainly to drinking in clubs and bars. This was, in fact, the figure quoted by the young man on the Suze Orman program.![]()
Over a working lifetime from 21 to 67 years of age this amounts to over a – staggering – $220,000 on alcohol.
But the financial cost is actually much greater.
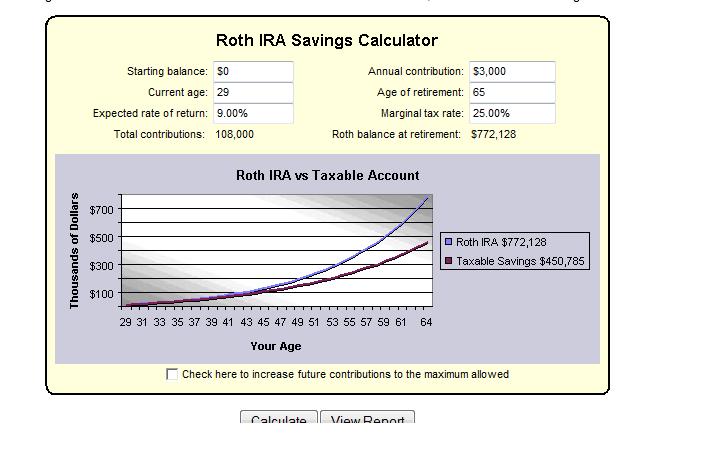
Suppose the $400 each month is invested instead in a Roth IRA with an annual return of 8% per annum.
At age 67, after years of investing $400 each month from the age of 21, the accumulated savings amount to $2,290,000: tax free.
 These are today’s dollars, so we have to think about inflation. Currently that’s low, but it might, and probably will, rise in the future. By the same token the return on the Roth IRA will also likely rise as inflation rises.
These are today’s dollars, so we have to think about inflation. Currently that’s low, but it might, and probably will, rise in the future. By the same token the return on the Roth IRA will also likely rise as inflation rises.
So let’s say a 21 year old does not put $400 each month into a Roth IRA but spends that $400 on alcohol until, at the age of 30, they decide to change their ways and start saving for their retirement.
Now the $400 each month in the Roth IRA is being invested for 9 less years. Not so bad, you think: this person is still young.
The accumulated savings from 30 to 67 yeas of age is now $1,087,000: again, tax free.
By drinking for 9 years the young person has lost over 1,200,000 tax free dollars.
The drinks in those 9 years cost $43,200.
So a drink that, on the face of it, costs $10 with tip in that person’s 20s, in fact cost them over $278 in lost savings.
The $10 drink effectively costs $278.
That’s the price you are really paying when you are young.
Just one more reason, by the way, that G.V. Ramanathan is wrong: quantitative literacy is important for everyone.