Teaching a range of mathematics: content and development
Posted by: Gary Ernest Davis on: October 13, 2010
The topic of this Thursday’s #mathchat on Twitter looks like being : “Does the nature of mathematics change as students get older or is it only the teaching methods that change?” This topic is the current runaway favorite as of Wednesday morning.
So this morning I’m trying to get a head start on thinking about this topic.
The nature of mathematics
Before we can sensibly discuss whether the nature of mathematics changes as students get older, it would help to have some idea in our minds of what it might be that is changing: what, in other words, we mean by “the nature of mathematics”.
Now this could get very philosophical indeed, so to avoid lengthy philosophical debates about “what is mathematics?” let’s focus on what might be the intent behind the #mathchat question. Let’s begin by looking at a specific example or two, always a good idea to anchor our thoughts. Let’s compare counting with trigonometry. Is this a real change in the “nature of the mathematics” that students learn, or is it more about different methods of teaching?
What is the nature of the mathematics involved in counting? And what is the nature of the mathematics involved in trigonometry?
Counting
 Many students come to school with some counting skills. Teachers regularly restrict counting to smaller numbers – typically up to 20 – in the earliest year at school, although many children are already familiar with much larger numbers such as one hundred, one thousand, and one million. One 4 year old boy in England told me that $2,500 was a big number. When I asked why he said because that’s what his mum paid for her car. Some 4 and 5 year olds already know about infinity.
Many students come to school with some counting skills. Teachers regularly restrict counting to smaller numbers – typically up to 20 – in the earliest year at school, although many children are already familiar with much larger numbers such as one hundred, one thousand, and one million. One 4 year old boy in England told me that $2,500 was a big number. When I asked why he said because that’s what his mum paid for her car. Some 4 and 5 year olds already know about infinity.
Counting always involves establishing one-to-one correspondences. This is as true when kids are counting their steps as they walk down stairs as it is when Galileo showed there are as many squares of whole numbers as there are whole numbers.
Kids first learn number names, in order, and learn to say them as they point at, or touch, objects in order to answer the question: “How many?” Then children undergo a process of development in counting, the details of which are largely unknown to early childhood classroom teachers. This development includes such things as being able to count hidden items, being able to count-on from a given number, and being able to count in units, to be able to answer questions such as “If I counted by 2’s to 24 how many times would I have counted?”
What is the “nature” of this mathematics of counting? Essentially it boils down to ever more flexible ways of establishing one-to-one correspondences.
Think about that for a moment: the mathematics of counting is the development of ever more flexible ways of establishing one-to-one correspondences.
Development! Development? since when has “development” been part of the topics of mathematics, of the “nature” of mathematics? Actually, since forever. Since Pythagoras and his school discovered that the square root of 2 is not commensurate with counting numbers, since algebraists in Italy discovered their correct formulas lead to the square root of negative 1. The content of mathematics has always been about personal and historical development of new ways of thinking and new ways of looking at old things. It’s only textbook revisionism that portrays mathematical content as devoid of human development. The reality is that mathematical content is all about human development, both personal and historical.
Trigonometry
Students usually learn trigonometry in the context of triangles: calculating lengths or angles of triangles. This is generally not a good idea: the standard trigonometric functions sin and cosine are called the “circular functions” for a good reason:
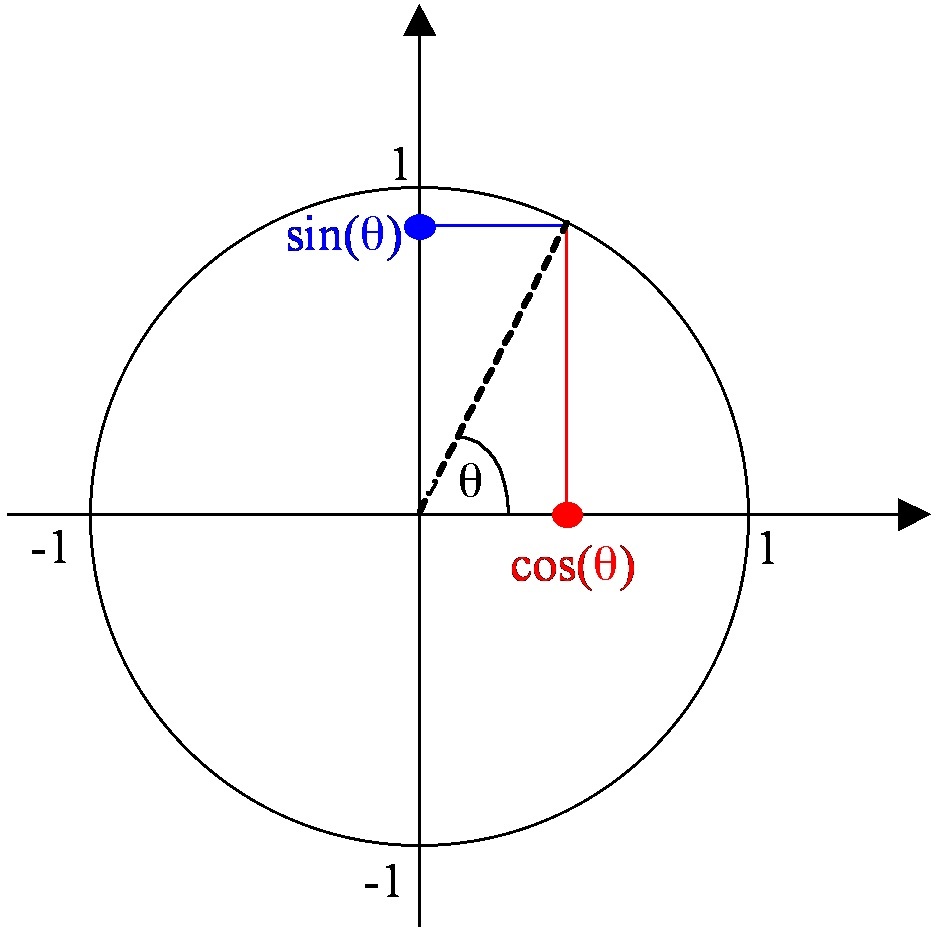
Circle of radius 1, with sin and cosine of an angle shown as vertical and horizontal projections of the end-point of the radius vector
What is the “nature” of trigonometry that students are expected to learn? In my experience, what passes for mathematical content in trigonometry are the slogans “sin = opposite/hypotenuse, cosine = adjacent/hypotenuse, tan = opposite/adjacent“. Of course these rote-memorized slogans make it difficult to see where sin and cosine will be positive or negative, whereas simply looking at the unit circle picture tells us. Proved we are familiar with Pythagoras’s theorem on right-angled triangles we can also “see” immediately that for all angles
.
 What is the “nature” of the mathematics that students are engaged with in trigonometry? Is there a developmental aspect to this as well?
What is the “nature” of the mathematics that students are engaged with in trigonometry? Is there a developmental aspect to this as well?
Early travelers used trigonometry to navigate the oceans and their early calculations soon evolved into spherical trigonometry, a topic not usually discussed in school or college mathematics. Knowledge of trigonometry traveled slowly from middle-eastern and Indian societies to Europe. European mathematicians and scientists were largely ignorant of trigonometry in the century. So there was a great deal of historical development around the topic of trigonometry.
What about personal development, for an individual student? A salient point about development is that viewed from afar it has the appearance of stages, or levels. Students seem to progressed through fairly well-defined stages of development. Of course looked at in fine detail development is nothing like that at all: it is messy, progressing in fits and starts, with lots of regression, and only a general overall appearance of permanent change after a long enough time.
Trigonometry focuses student understanding of angles, and of measurement both of angles and lines – both straight and curved. The circular functions are essentially making straight what is curved. Students are used to measuring angles the ancient, and arbitrary way, in terms of degrees. The circular functions introduce the possibility of another, more intrinsic angle measure: the length of arc swept out by an angle. This, of course, is radian measure which even engineering students do not understand well enough.
Teaching methods
Of course we need to have some idea of what we mean by “teaching methods”: if we are to be in a position to address the #mathchat question.
Teaching methods are, in my experience as a mathematician, mathematics educator, and teacher educator, those means and ways a teacher can utilize to begin to teach a particular mathematical topic. In my engagement with prospective and in-service teachers I have always focused on student development. What this means in practice is assessing where students are in their thinking, and then designing means to assist them to develop. Significant areas of mathematics where I have used this approach are children’s counting (Steffe counting types) and geometry (van Hiele levels).
My answer?
My tentative answer to the #mathchat question: “Does the nature of mathematics change as students get older or is it only the teaching methods that change?” is: Neither.
Mathematics is, and always was, about changing understandings of number, space, and arrangement. Teaching methods should, in my view, always be about developmental issues in students’ deepening engagement with these broad aspects of mathematics. As students get older the only thing that does seem to change is the pace at which this development is expected to take place.
Postscript
Once again Ryan R (@suburbanlion) has written a beautiful post that has given me pause for thought. I congratulate him on this post. He argues that the nature of mathematics DOES change for a student, as they encounter truly surprising mathematical developments. And with that I agree. I think it is implicit in my view that development is an important part of all mathematical topics: that we cannot separate out “geometry”, number theory”, calculus” and pretend these are cut and dried subjects that never underwent historical development, and do not imply personal development. So, I agree with Ryan that the nature of mathematics does change for a student over time.
Depression and problem solving in mathematics: the art of staying upbeat
Posted by: Gary Ernest Davis on: October 12, 2010
@reasoningmind I agree. But the best of us cannot always solve problems. Trick is to learn how to stay upbeat. Teachers job IMO #mathchat
x
Of course, by “us” here I mean the human race, and not any one particular individual. If problem solving is seen as a race or a competition, then yes, of course, there will be many problems that will defeat even the most talented students, and they may well become disheartened. Less mathematically able students can become disheartened a lot earlier.
 Probably the most upbeat mathematical problem solver on this planet is Terry Tao. Chances are no one has ever been a better mathematical problem solver than Terry. He tackles some of the deepest and toughest mathematical problems there are, and manages to stay very upbeat about it all, so there’s something to be learned from him about a positive attitude to problem solving and to mathematics in general. Terry wrote a helpful blog post “Solving mathematical problems“. He recommends playing with a problem:
Probably the most upbeat mathematical problem solver on this planet is Terry Tao. Chances are no one has ever been a better mathematical problem solver than Terry. He tackles some of the deepest and toughest mathematical problems there are, and manages to stay very upbeat about it all, so there’s something to be learned from him about a positive attitude to problem solving and to mathematics in general. Terry wrote a helpful blog post “Solving mathematical problems“. He recommends playing with a problem:
“I find that “playing†with a problem, even after you have solved it, is very helpful for understanding the underlying mechanism of the solution better. For instance, one can try removing some hypotheses, or trying to prove a stronger conclusion.”
He also strongly advises that you ask yourself dumb questions – and answer them!
You may so it’s all very well for Terry Tao to be positive about mathematical problems: he’s shown a remarkable ability to solve hard mathematical problems since he was very young. That’s not how it is for me or for my students.
Ed Burger writes: “… my math teacher taught me how to ask questions and not give in until I was able to understand. My math teacher taught me how to look at the world and see it in a crystal focus. My math teacher taught me how to think and create.”
So how can mathematics teachers help students feel positive and upbeat about solving mathematical problems – from simple to hard? How can, as ReasoningMind suggests, even the best mathematics teachers overcome the dispirited feeling students get when they cannot solve mathematical problems?
I have a few suggestions to offer – only a few – but I hope they may go some way to helping classroom teachers work to keep an upbeat spirit for all students in their mathematics classrooms.
Ask yourself dumb questions – and answer them! (Terry Tao’s advice)
This is about the simplest and most useful piece of advice I know for keeping upbeat about mathematical problems. Here’s a good way to implement it. Start a diary for a problem. Use an exercise book, or a word document on a computer, in which a student records what they found each day they worked on the problem; a summary of calculations they did and conclusions they reached. The next time the student begins work on the problem read the previous diary entry and get them to ask the simplest dumbest question to which they do not yet know the answer – and set about answering it! This way, progress becomes palpable.
This assumes that the problems students are working on will not necessarily be expected to be completed in a single class period. For harder problems, limiting students’ working time to a single class is highly likely to lead to frustration, depression and a general air of being dispirited. Not good! Keep the problems that are expected to be completed in a single class session or for a set homework period, to routine problems.
Reduce cognitive load (John Sweller’s advice)
 I wrote in an earlier post about my conversion to John Sweller’s viewpoint on problem solving. This is about reducing the demands on students’ working memory. Teachers of mathematics need to think about and analyze the problems they set for students to see – as a best estimate – how certain problems might be stressing working memory of their students. Teachers need to instruct students in ways of reducing cognitive load – the demand on working memory made by certain problems. When most problems a student tackles stress that student’s working memory beyond its capacity the student will soon give up, feeling defeated. The teaching issue is that this feeling of defeat never had to happen if the teacher had instructed students in ways of reducing the load on working memory.
I wrote in an earlier post about my conversion to John Sweller’s viewpoint on problem solving. This is about reducing the demands on students’ working memory. Teachers of mathematics need to think about and analyze the problems they set for students to see – as a best estimate – how certain problems might be stressing working memory of their students. Teachers need to instruct students in ways of reducing cognitive load – the demand on working memory made by certain problems. When most problems a student tackles stress that student’s working memory beyond its capacity the student will soon give up, feeling defeated. The teaching issue is that this feeling of defeat never had to happen if the teacher had instructed students in ways of reducing the load on working memory.
The problem might be really, really hard
Some years ago my colleague Elena Steencken at Rutgers came into my office excited to tell me how the students and teachers in her group had found a beautiful pattern for a counting problem. I cannot remember the exact formulation of the problem but I do recall what happened next. I must have frowned because Elena said: “Uh, oh! The look on your face!” I asked what she meant, and she said I looked worried. Well, I was was worried. I thought about the problem later that day and realized it was a reformulation of the problem of counting self-avoiding walks of a given length.
This is a famous, very, very difficult problem in mathematics. It is very unlikely that a group of teachers and students would solve it in an hour or two, and it was certainly not true that Elena’s simple algebraic formula was correct. I told her so the next day, and she said they had tested it for various cases. I asked her to test it for the next case where I knew the answer had been worked out in detail: her formula did not agree with the known answer!
The moral: really, really hard problems are lurking everywhere in mathematics. You may have stumbled across one. Check your answers and then ask a professional mathematician if they know, or knows someone who knows, something about the problem. This is not failure – it’s real authentic learning. It is discovering facts about the nature of the mathematical landscape – mathematical reality as distinct from textbook knowledge. It’s fun, it’s exciting, and anyone can do it. But beware that your problem might be genuinely really hard. Understanding why develops mathematical maturity.
 Here’s an example of how easy it is to misunderstand the difficulty of a problem. The Tower of Hanoi problem is a well-known and often used example in problem solving for upper elementary and middle school students. Often enough students will come up with a recursive solution to the tower of Hanoi problem. What have they solved? They have shown, essentially that with 3 pegs and n disks on 1 peg it is possible to shift all the disks, following the rules of moving only one disk at a time and never putting a larger disk on a smaller one, to another peg in
Here’s an example of how easy it is to misunderstand the difficulty of a problem. The Tower of Hanoi problem is a well-known and often used example in problem solving for upper elementary and middle school students. Often enough students will come up with a recursive solution to the tower of Hanoi problem. What have they solved? They have shown, essentially that with 3 pegs and n disks on 1 peg it is possible to shift all the disks, following the rules of moving only one disk at a time and never putting a larger disk on a smaller one, to another peg in moves. What they have not done is to show that this is the shortest number of moves possible: that takes a different, more subtle argument.
Now what happens when we move to the 4-peg version of the Tower of Hanoi? Many people suspect, but to this day no one knows, the correct answer for the shortest numbers of moves to complete the puzzle. That is hard mathematics, arising from a simple puzzle.
