Mathphobia: its existence, severity and possible remedy
Posted by: Gary Ernest Davis on: October 11, 2010
A recent Twitter #mathchat was devoted to mathematics phobia – “mathphobia” for short. The question addressed was: ” Does ‘mathphobia’ exist – how do we deal with it?”
My experiences with mathphobia
“I’m unusual I have mathphobia”
Several years ago I taught mathematical methods to elementary pre-service teachers in Washington State. These were students majoring in elementary education who were just about to begin their first classroom experiences and were enrolled in a mathematics methods class. I also taught mathematical methods to a group of older pre-service elementary teachers who were changing careers and undergoing teacher training through an 18 month Masters in Teaching program.
As is my custom in these courses, I asked students in a class to introduce themselves to each other, and to give us all some information about their backgrounds. One young woman responded, when it was her turn to tell us about herself, that she was unusual in that she was mathphobic. I used this opportunity to ask the class who else would regard themselves as mathphobic. More than half the class of about 30 students raised their hands. I then said: “Please only leave your hand raised if by mathphobic you mean shaking with fear or wanting to vomit when you have to do mathematics”. Not one person lowered heir hand.
Think about that for a minute: over 15 young adults, preparing to go into schools and teach elementary age children, shaking with fear or wanting to vomit when they had to do mathematics. Doesn’t bode well for young children learning mathematics does it?
“I need to vomit when I think about fractions”
My colleague Robert Hunting used also to teach mathematical methods to pre-service elementary teachers in Melbourne, Australia. One semester when he prepared to discuss teaching fractions to these pre-service teachers one of the students left the room hurriedly. Upon her return she told Robert she had to go to the bathroom to be sick. Robert asked if she was alright, and she responded that she feels violently ill when she has to think about fractions.
” I had a bad experience in a mathematics class”
Again in Melbourne I filled in for a colleague on leave and took her elementary pre-service mathematics class. One young woman in the class constantly talked over me when I was trying to make a point to the class. When I brought her constant chattering to her attention she asked why I was picking on her. I explained I wasn’t and that her talking interrupted my conversation with the rest of the class. At that point her friend came to her aid and again asked me why was I picking on this student. I repeated that she continually talked over me and over other students. The student in question was horrified and said she never did any such thing. I then indicated an older male student and said to her: “You talked all the way through his presentation last week.” She looked mortified and was even more upset when the male student nodded in agreement with me. The young woman then burst into tears, and told me she had a terrible experience once in mathematics class, and she now had a fear of mathematics. When I asked what the experience was she said she could not talk about it.
I was skeptical that her poor performance in mathematics class was radically different to her other classes until I heard her read beautifully, with excellent comprehension and clear expression. It was then clear to me and to the rest of the class that she had been traumatized and now had a morbid fear of mathematics.
“Here, catch the Stupid Rock”
At Washington State one of my professional colleagues told me about an elementary teacher he knew of who had a large papier-maché rock in his classroom labeled “STUPID ROCK”. When he asked the class a mathematics question he would throw the rock to the child who, in his judgment, gave the stupidest answer. Imagine going home after school and telling your mother, when she asked what you learned in school that day, that you are stupid at mathematics. This is nothing less than child abuse.
How bad is the fear?
Many years ago when I was at Simon Fraser University in Vancouver BC, Canada, I stepped into an elevator to descend to street level and go home. The elevator dropped as stepped into it – maybe a foot or so. My heart seemed to stop and I shook with fear of falling. All was well, however. I descended without incident. Next morning as I entered the building I went to use the elevator again but my legs would not move: I was frozen to the spot. It took my several months of working hard to overcome panic and retraining my body memory before I could get into an elevator again.
My stories about students with fear of mathematics are jut anecdotes. Yet I have hard such stories from many mathematics educators in Australia, the United States, England, and several other countries. I’ve heard them sufficiently often that I believe this morbid fear of mathematics – mathphobia – to be a very real and wide spread condition.
A couple of people made suggestions on #mathcat as to what mathphobia might be:
What can we do about a morbid fear of mathematics?
Postscript
Why are there triangles in buildings and bridges?
Posted by: Gary Ernest Davis on: October 7, 2010
When you look around at the geometry of the built environment – buildings and bridges, among other structures – you see quite a few triangles:

Why is this?
What is it about triangles that we see them in built structures? Do they look pretty, and are there for ornamentation? Are the architects and builders showing us they know some geometry?
The major reason for triangles appearing so often in built structures is that triangles are rigid.
Being rigid means that when the lengths of the sides of a triangle are specified, the angles are determined already.
This is quite unlike a quadrilateral (a four-sided polygon), for example, which can have a range of different angles for a given set of side lengths:
What is the reason that a triangle is rigid?
Looks look in detail at a triangle, it’s side lengths and angles:
The corners of this triangle are labeled A, B, C; the side lengths are a, b, c; and the angle measures are .
To assist us in analyzing this triangle let’s put a coordinate system on the triangle as follows:
This is by no means necessary, but it will help us quite a bit in working out why the triangle is rigid.
Since we have a coordinate system, with corner C conveniently located at the origin of that system, let’s put coordinates at the corners:
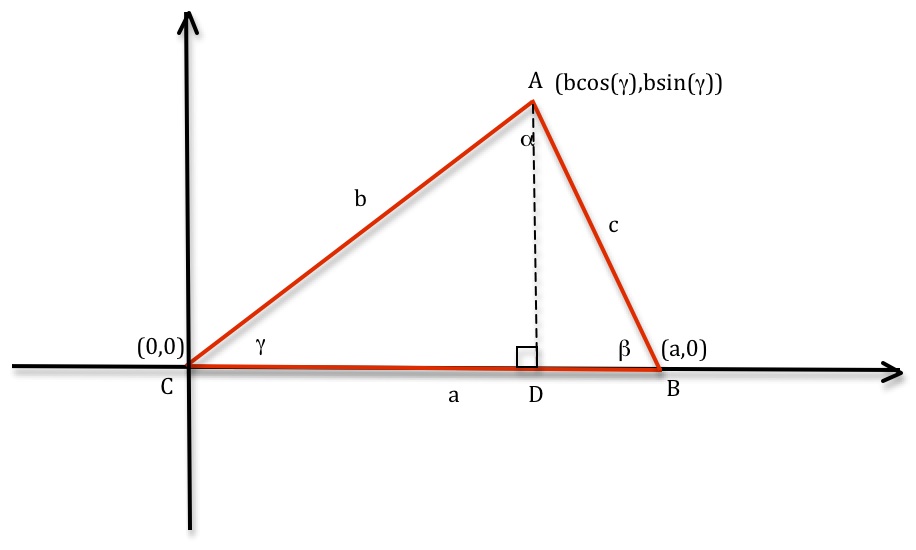 The coordinates of the corner A come from looking at the sin and cosine of the angle
The coordinates of the corner A come from looking at the sin and cosine of the angle in the right-angled triangle ADC.
Now from Pythagoras’s theorem we see that .
Expanding the right hand side of this equation we get .
Because we get
.
This means and therefore the angle
is determined by the side lengths a, b, c.
The same is true for the angles so the triangle is rigid: its side lengths determine its angles.