When academic textbook prices drop to $0.00 what will publishers do?
Posted by: Gary Ernest Davis on: October 6, 2010
Technology is like a universal acid to societal norms – it eats away away at all existing structures and modes of operation. People have lost jobs because technology has put them out of work, just as technology has created new jobs for others. Work, business and education are in high states of flux as more and more human activities are impacted by technology. And the pace is picking up, not slowing.
College students presently pay very high prices for text books.
This semester I am teaching Calculus 3, and the book the Department of Mathematics chose for our calculus sequence is by James Stewart, published by Brooks Cole and into its 6th edition. It’s priced at $224.95 (amazon.com price $165.45 + postage, at time of writing) and is a large book at 1344 pages. That works out at a little under 17 cents per page for the publisher’s list price and a little over 12 cents per page for the amazon.com price. The per page cost may not be excessive, but the initial cost is high for many college students or their parents. This is a book that is used for 3 semesters, so one might argue that at around $75 per semester it’s not overly expensive.
The other course I am teaching this semester is differential equations. A book I like as do many of my colleagues is Differential Equations: A Contemporary Approach by Paul Blanchard, Robert L. Devaney, Jong-Eao Lee Glen R. Hall, and Jong-Eao Lee. It is currently priced at $148.44 +postage on amazon.com. Instead I chose as a text this year Ordinary Differential Equations by Morris Tenenbaum and Harry Pollard, published by Dover Books, listed at $24.95 and currently $16.47 + postage on amazon.com
Another colleague and I work to find good texts at low prices.
Some months back this got me to thinking about how we might reduce the price of mathematics texts to very low prices – to $0.00 in fact.
One way to do this is for academic authors to simply give their books or notes away: to make them freely available to students in electronic format, as pdf or html files. Authors who do this are not going to get rich from royalties this way, but do it because they feel a responsibility of care for students. A stunning example of this – but by no means unique – is Paul’s Online Math Notes, where you can find beautifully written accounts of Algebra, Calculus I, II, II, Linear Algebra and Differential Equations.
As I thought about this issue it struck me that placing advertisements in text books might be a way to reduce the price to $0.00. Advertisers could obtain audited sales figures, and ads could be targeted to a well-defined audience. As I thought about this idea I came across bookboon.com who have already implemented it!
Open source textbooks are increasing in availability but have not yet really begun to take over from the high priced commercial texts. One reason for this, in my view, is that teachers – school and college – are addicted to the newest shiniest editions of texts pumped out by publishers. New editions appear every few years and students are told fairy tales such as “You need the new edition because the homework for chapter 3 is on a different page.”
The capitalist system is great when it works. It’s not great when publishers and authors are getting rich at the expense of students and their parents. Most students don’t want the texts they buy – they are told they have to buy them. It’s a captive market, and the teachers are cooperating with publishers to keep students enslaved to this expensive system.
The single biggest technology issue that will change this state of affairs, in my view, is cheap or open source homework grading systems that are relevant to a wide range of texts. Teachers care much more about not grading homework than they do about shiny new editions of text books. Current online homework grading systems for mathematics are relatively cheaper than textbooks – $37Â for Stewart’s Calculus. But if textbook prices were forced to fall you can bet prices for online grading systems would rise.
Advertisements in books can, and my guess is will, bring the price of textbooks down to $0.00. Then publishers will move – as they already are doing – into other profitable areas such as online grading systems, and videos of exemplary teaching.
It will take intelligence and skilled programming to produce an online grading system for mathematics that could grade across a variety of text sources and topics. Yet it could be done. In my view it should be done for the sake of care for our students.
Astonishing consequences of naive thinking about sets: Cantor's diagonal argument
Posted by: Gary Ernest Davis on: October 4, 2010
I have mentioned in several posts now that many people do not think it is problematic to bundle all the counting numbers together in a set: the set of all natural numbers, denoted .
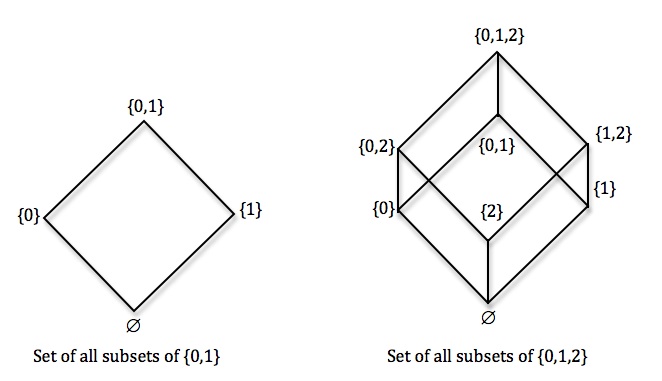
Another apparently harmless naive thought about set formation is that one can always construct the set of all subsets of a given set. For a set the set of all subsets of
is denoted by
. For simple sets such as
we can easily visualize
and the relations between its elements – i.e. the subsets of
:
where denotes the empty set, and rising lines indicate the set below is a subset of the set above.
Perhaps someone might balk at reflecting on a set consisting of all subsets of the natural numbers, yet there is a simple device to make this construction seem plausible.
The set of all subsets of a set
is in one-to-one correspondence with the set of all functions from the set
into the two element set
.
This correspondence is established as follows: for each subset define a function
by
; conversely, for each function
define a subset
of
by
.
So to think about all subsets of the set of natural numbers, it is equivalent, to think about all functions
.
Such functions give a value of for each natural number, and so correspond to sequences
where each
is either
.
Georg Cantor established the following extremely simple, yet devastating, result: for any set for which the set
of all subsets of
exists, there cannot be a one-to-one correspondence between
and
.
The argument is incredibly simple as it is elegant.
A one-to-one correspondence between and
is established by a function
that is invertible. Cantor shows that no function
is invertible. Here’s how he does it: let
be a function. Define the subset
by
. Then, for every
exactly when
. Because either
for every
it follows that
for all
, and therefore the function
is not invertible.
This is Cantor’s famous diagonal argument. Quite simple and relatively uncontroversial. Yet is has a devastating and astonishing consequence.
Given that, naively, we can always form the set of all subsets of a set
, we see that the set
of all subsets of natural numbers cannot be put into one-to-one correspondence with
itself. Because the mapping
from
is one-to-one, but not invertible, the set
has greater cardinality than that of
. That is, the set of all subsets of natural numbers is a set of greater order of infinity than the set of natural numbers itself.
What now stops us from forming the set which, by Cantor’s argument, has a higher order of infinity again, and so on, and so on(ad infinitum and beyond …) ? This is a glimpse of Cantor’s paradise from which, David Hilbert averred, no one shall expel us.