The strangeness of mathematical language
Posted by: Gary Ernest Davis on: September 30, 2010
The four branches of arithmetic: ambition, distraction, uglification and derision. The Mock Turtle
Polylaterals
We all know what a triangle is: its a closed figure with 3 sides.
 But the triangle’s generic name sounds like it should have 3 angles: TRI-ANGLE. Well, of course, it does have 3 angles, one opposite each of the 3 sides. So why do we call a closed figure with 3 sides a triangle? why don’t we call it a TRI-LATERAL, for 3 sides?
But the triangle’s generic name sounds like it should have 3 angles: TRI-ANGLE. Well, of course, it does have 3 angles, one opposite each of the 3 sides. So why do we call a closed figure with 3 sides a triangle? why don’t we call it a TRI-LATERAL, for 3 sides?
The next figure along, so to speak, would be a four sided figure which we do indeed refer to as a QUADRI-LATERAL, for 4 sides.
But why don’t we call it a QUADR-ANGLE? Because that name is reserved for a special sort of 4-sided figure associated with buildings. It’s generally rectangular – a square or oblong (now there’s a strange word) – surrounded by or abutting a building:
Hang on, how does rectangular mean a 4-sided figure, especially a square or an oblong? Shouldn’t RECT-ANGULAR mean right angles? Yes it does, and a plane figure with all right angles is a square or an oblong (but also known of course, as a rectangle).
Of course if we lived on a strange place, such as a sphere – thank goodness we don’t! – we could have a triangle with all angles right angles, so qualifying as a rectangle with only 3 sides:
So what’s an oblong, and who came up with a name like that? Well word on the street is that the name comes from OB (meaning quite, very, or rather) and LONG (meaning, … long). Someone named this around 1375–1425 in Middle English. So an OB-LONG is a rather long rectangle, meaning it’s not a square. But I think this use of “OB” is a little strange, because OB also means “in the way” as in OB-STINATE (in the way + stand), OB-JECT (in the way+ throw), and “against” as in OB-DURATE (against + hard). The OB seems a little bit of an overworked prefix.
So moving on we come to a 5-sided closed figure which, of course, we call a PENTA-LATERAL, meaning a 5-sided figure. Except we don’t: it’s a PENTA-GON meaning 5-angles. Hang on, that being the case, why isn’t a triangle known as a TRI-GON?
The next figure along would be a SEXA-GON – a 6-sided figure – except it’s not it’s a HEXA-GON, because we try to keep sex out of geometry.
So on we go now with lots of GONS – septagon, octagon, nonagon, … and not another LATERAL in sight.
Polynomials
The quadratic polynomial was being interviewed about his function in life:
INTERVIEWER: “So, p(x), I understand that you’re not often satisfied?”
p(x): “That’s correct. Only a couple of numbers satisfy me.”
INTERVIEWER: “I understand that is one of those numbers.”
p(x): “Yes. I find  very satisfying.”
INTERVIEWER: “Is that a bit irrational?”
p(x): “It’s quite irrational, but there’s no accounting for what satisfies a polynomial.”
INTERVIEWER: “And are there any other numbers that satisfy you.”
p(x): “Well there’s of course.”
INTERVIEWER: “That’s also a bit irrational, isn’t it.”
p(x): “Quite irrational, but there you are. I’m not easily satisfied.”
INTERVIEWER: “Are there any other numbers that satisfy you?”
p(x): “No, that’s it.”
INTERVIEWER: “Well there you have it – the strangely unsatisfying life of a quadratic polynomial. The numbers that satisfy polynomials are known as roots. Polynomials do not have many roots, being satisfied by a mere handful of numbers. This is a situation well understood by Australians.”
Abscissa
This just means the line in a Cartesian coordinate system over which the independent variable ranges, usually drawn horizontally.
The word AB-SCISSA comes from AB (meaning off or from) and SCINDERE (meaning to cut). So an abscissa is supposed to be something that cuts something off from something else. This was apparently named in 1694 by some dude. Nowadays you might just want to say: “the independent variable axis” or “the horizontal axis”. But if you want to appear knowledgeable and superior, especially if you are a high school mathematics teacher, or if you are a student out to impress your teacher, then”abcissa” will do it.
What is a gerbe?
I hoped you wouldn’t ask that. Wikipedia sums it up as succinctly as anywhere else:
“A gerbe on a topological space X is a stack G of groupoids over X which is locally non-empty (each point in X has an open neighbourhood U over which the section category G(U) of the gerbe is not empty) and transitive (for any two objects a and b of G(U) for any open set U, there is an open set V inside U such that the restrictions of a and b to V are connected by at least one morphism).”
Well, of course! Now you put it that way it’s more or less …. still unclear!
Why do mathematicians do this? Is it just to appear smug and superior to the rest of the world. Well no, but there is an element of that:
Piotr: “Heinrich, I think that gerbe you were talking about earlier must be locally trivial.”
Heinrich; “Why, yes, that’s so Piotr. Did I not make that clear?”
Let’s face it: who among us would not love to able to casually toss off such an apparently abstract discourse?
But not all mathematicians are just tossing off abstract discourse:
Heinrich: “So let’s take a transitive locally non-empty stack of groupoids over a torus …”
Michael: ” You mean a gerbe?”
Heinrich: ” Yes, that’s right. A gerbe on a torus.”
So you can see that it helps Heinrich not to have to say “a transitive locally non-empty stack of groupoids over a topological space” but to be able to say, simply, “a gerbe” instead. What a time saving shortcut!
This habit of strange names in mathematics comes from the relatively rarefied practice of high-octane advanced mathematics. It’s a matter of convenience, and quite different to when someone says “His Royal Highness, the Prince of Wales” when what you know they mean is “Charles Windsor”, or at least, “Charles Windsor in the capacity bestowed upon him by his mama.”

Thanks to proper naming conventions, no-one would mistake the Prince of Wales (a.k.a. Tywysog Cymru) for a gerbe.
There’s much more I could write about strange mathematical names … and at some point in the future I probably will.
Postscript
flyingcoloursmaths (Colin Beveridge) points out that we do see trigon in trigonometry, from “trigonon” + “metria”. This brought home to me the English-centered view of mathematical words I was using, as if all mathematics is written in English – which it was not, and is not. The Greek word for triangle is Ï„Ïίγωνο, and for quadrangle is τετÏάγωνο.
In french a triangle is a “triangle” and in German it is a “dreieck”; here “drei” is “three” and “ecke” is “angle”.
How do people in different languages refer to triangles and other polygons, I wonder.
By the way, the English translation of “gerbe” is “sheaf”, but that word was already in common use in mathematics when Jean Giraud introduced the definition of a gerbe in 1971.
"See, that’s the sickness right there. You find math fun, don’t you?"
Posted by: Gary Ernest Davis on: September 27, 2010
The title of this post comes from an interview with “Punk Mathematics” author Tom Henderson.
There are lots of websites with the words “Fun” and “Math” in their title. But many of these sites are just clowning around to be funny without making the math itself fun.
Bubblz
Bubblz is a math clown with a difference.
There’s no doubt that Bubblz is a clown. Yet, it seems to me that Bubblz is funny, entertaining, educates, and makes the math humorous too.
Martin Gardner: The man who made mathematics fun
Martin Gardner, who died this year, was a prolific writer on mathematics and science.
He seemed to induce people to think that mathematics is fun:
Inigo Montoya wrote, May 23, 2010:
Go well, Mr Gardner. For me, you made mathematics real. You made it fun. I can’t thank you enough.
MikeMoore wrote, 7:20 PM Saturday, May 22, 2010:
RIP Mr. Gardner…you introduced me to the world of math & science, and taught me it could be fun too! Without you I would have never considered studying mathematics, computer science, or linguistics…
Thank you!
Anon wrote, 7:59 AM Sunday, May 23, 2010:
RIP Master Methemagician Gardner. Thank you for allowing my students to discover the magically fun side of math!
Scientific American profile of Martin Gardner
A mathematician plays and has fun
Paul Lockhart, writes in “A Mathematician’s Lament“:
” …if I’m in the mood to think about shapes— and I often am— I might imagine a triangle inside a rectangular box:
I wonder how much of the box the triangle takes up? Two-thirds maybe? The important thing to understand is that I’m not talking about this drawing of a triangle in a box. Nor am I talking about some metal triangle forming part of a girder system for a bridge. There’s no ulterior practical purpose here. I’m just playing. That’s what math is— wondering, playing, amusing yourself with your imagination. For one thing, the question of how much of the box the triangle takes up doesn’t even make any sense for real, physical objects. Even the most carefully made physical triangle is still a hopelessly complicated collection of jiggling atoms; it changes its size from one minute to the next. That is, unless you want to talk about some sort of approximate measurements. Well, that’s where the aesthetic comes in. That’s just not simple, and consequently it is an ugly question which depends on all sorts of real-world details. Let’s leave that to the scientists. The mathematical question is about an imaginary triangle inside an imaginary box. The edges are perfect because I want them to be— that is the sort of object I prefer to think about. This is a major theme in mathematics: things are what you want them to be. You have endless choices; there is no reality to get in your way.
On the other hand, once you have made your choices (for example I might choose to make my triangle symmetrical, or not) then your new creations do what they do, whether you like it or not. This is the amazing thing about making imaginary patterns: they talk back! The triangle takes up a certain amount of its box, and I don’t have any control over what that amount is.
There is a number out there, maybe it’s two-thirds, maybe it isn’t, but I don’t get to say what it is. I have to find out what it is.
So we get to play and imagine whatever we want and make patterns and ask questions about them. But how do we answer these questions? It’s not at all like science. There’s no experiment I can do with test tubes and equipment and whatnot that will tell me the truth about a figment of my imagination. The only way to get at the truth about our imaginations is to use our imaginations, and that is hard work. In the case of the triangle in its box, I do see something simple and pretty:
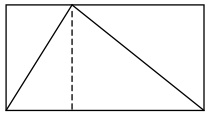
If I chop the rectangle into two pieces like this, I can see that each piece is cut diagonally in half by the sides of the triangle. So there is just as much space inside the triangle as outside. That means that the triangle must take up exactly half the box!
This is what a piece of mathematics looks and feels like. That little narrative is an example of the mathematician’s art: asking simple and elegant questions about our imaginary creations, and crafting satisfying and beautiful explanations. There is really nothing else quite like this realm of pure idea; it’s fascinating, it’s fun, and it’s free!”
Fun with problem solving
Several years ago I gave the following problem to a group of students enrolled in a pre-engineering course. A couple of them were adamant it was impossible to solve because the information given was not relevant to the solution. They persisted for about a half hour and when they got the answer there was much hilarity and incredulity that they could actually figure out an answer.
One day two people Erik and Deborah, meet in the street.
“Hello Erik, it’s been a while since I’ve seen you. How old are your 3 boys now?” asks Deborah.
Erik, knowing Deborah is a mathematician, poses a puzzle for her:
“When I multiply their ages I get 36.”
Rising to the challenge, Deborah sad she needed more information than that to work out their ages.
Erik pointed to a nearby house and said:Â “When I add their ages I get a number equal to the number of windows in that building.”
Deborah thought for a second, and said she still needed more information.
“OK”, said Erik, “my eldest boy has blue eyes.”
“Got it!” said Deborah, laughing.
How did Deborah work out the boys ages ?
Be careful! You might have fun!