Republic of Mathematics blog

Spring semester 2010 I ran a mathematical modeling course on protein-protein interaction networks in cells.

Interactions between proteins in cells are critical to the functioning of a cell.

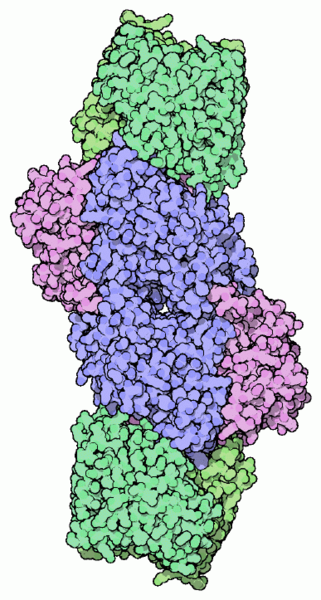
The bacterial nitrogenase enzyme is formed by a protein-protein interaction between two copies of two different proteins. One protein is shown in shades of green, the other in shades of blue and purple.

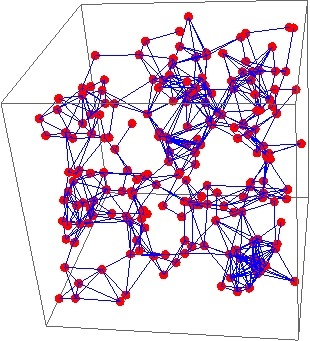
The collection of all proteins in a cell forms a network with the proteins as the points, or vertices, of the network, and interactions between proteins indicated by lines, or edges:

Network visualisation of the human cellular interaction network, where each point represents a protein and each blue line between them is an interaction.

In these networks an important role is played by cliques. These are collections of proteins in which each protein in the collection interacts with every other protein in the collection. In graph-theoretic terms, they are complete subgraphs. Finding cliques in protein-protein networks is a problem of biological significance (a, b, c)

The problem of finding cliques (=complete subgraphs) in a network -the clique problem – is NP complete, so if then there is no fast algorithm to solve this problem.

Leanne Silvia began as an honors student in our undergraduate computational science program when she was a freshman. Spring 2010 she was a student in the mathematical modeling course referred to above, and she became interested in the clique-problem, to the extent that she worked on it as a research project Summer 2010, as a student in our computational science program [lsilvia_siam2010poster].

Mathematica has in-built algorithms (in Combinatorica) to find maximal cliques. Leanne’s algorithm finds all cliques, and over a certain size of graph, does it faster than existing Mathematica algorithms. This Fall, as a beginning junior she will be presenting her research at the Wolfram Technology Conference in Champagne, IL. Her algorithm may prove to be especially useful to biologists working in this area.

x

Leanne is working now on applying her algorithm for finding cliques to random geometric graphs. These are graphs formed by placing a number of points – in a plane or in space – randomly, and joining points by an edge if they are “close” – i.e. within a specified distance of each other.

Random geometric graphs have, over the last few years, come to be regarded as a good model for protein-protein interaction networks. Therefore, any algorithm that finds all cliques in random geometric graphs – at least for a range of total number of points – will be of interest to biologists working on protein-protein interactions.

A random geometric graph in a unit cube: 200 uniformly random points, which are joined pairwise if they are less than 0.2 apart

In an earlier post, I wrote that my colleague Sigal Gottlieb was annoyed by her own approach at automatically solving the following problem – which she had asked of her elder son – via algebra, rather than thinking through the problem in a more direct way:

In a large group of children there are 3 boys for every 2 girls. 30 boys leave the group and then in the smaller group that’s left there are 2 boys for every 3 girls. How many boys and girls were there in the original group?

To give the same flavor of the problem but make it a little easier for her younger son, she asked him:

Two children Amy and Bob, each have collections of books. Bob has twice as many books as does Amy. Amy’s mother buys her 24 new books and then Amy has twice as many books as does Bob. How many books did Amy and Bob have to begin?

The second problem

Let’s look at the second problem diagramatically:

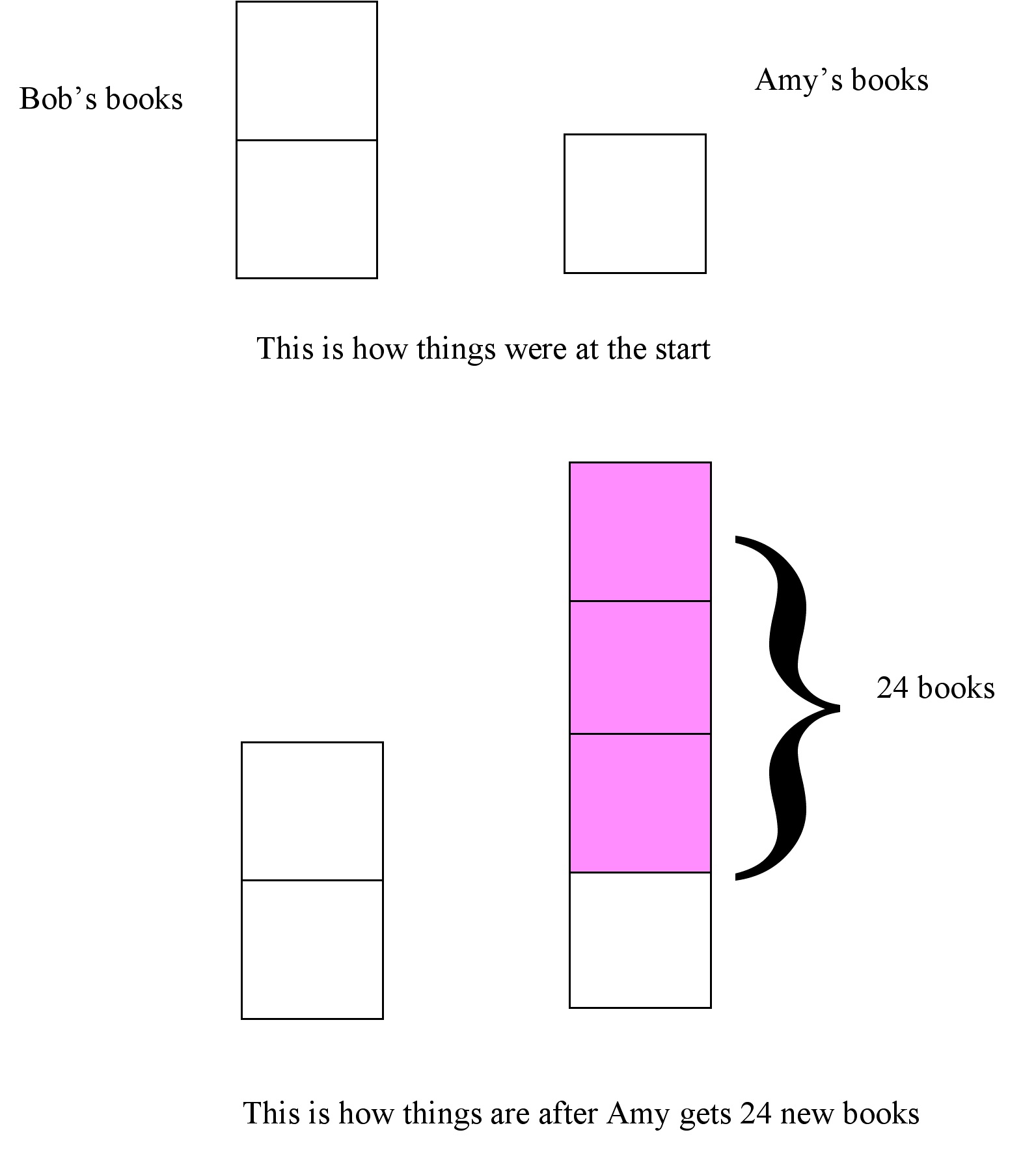In this diagram we imagine Bob and Amy’s books to be evenly distributed in boxes: each box holds the same number of books.

Bob has two boxes of books to Amy’s one box.

Amy then gets 24 more books.

Bob’s books stay the same so Amy has some more boxes.

In order to have a ratio of 2 to 1 Amy gets 3 extra boxes.

So 3 boxes, each with the same number of books, holds 24 books. Therefore 1 box holds 8 books.

So originally Bob, with 2 boxes, had 16 books and Amy, with 1 box, had 8 books.

The first problem

The first problem can be approached diagramatically in much the same way, but a little adjustment is in order because of the slightly more awkward ratio of 3:2

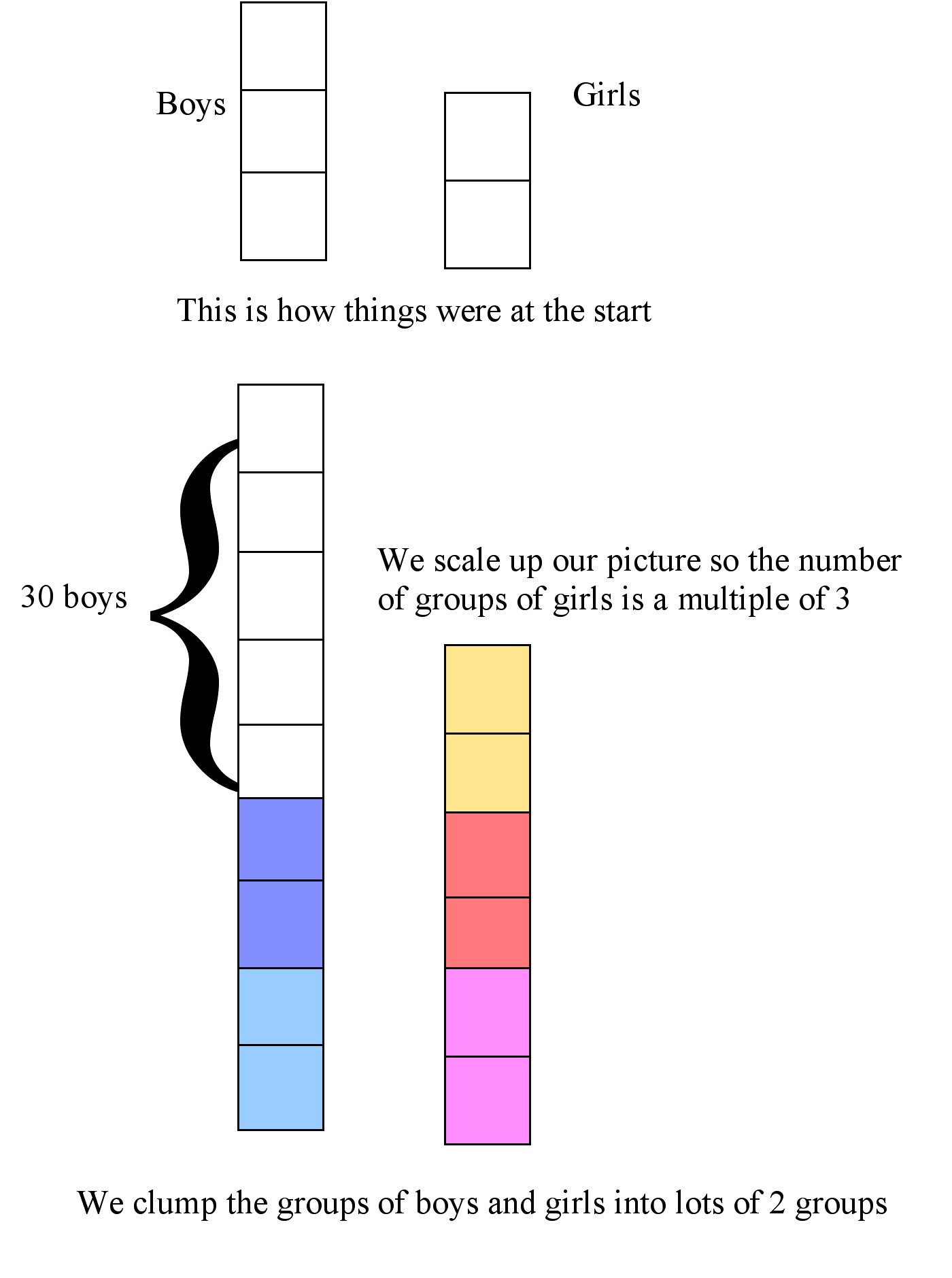In this diagram we begin with 5 equal size groups : 3 groups of boys and 2 groups of  girls.

We want to end up with a ratio the other way around, so one sensible thing to do is to scale up the picture by scaling the numbers of boys and girls by a factor of 3.

Then there are 9 groups of boys and 6 groups of girls – still a ratio of 3:2 for boys to girls.

Now let’s clump the groups into lots of 2, as shown by the coloring.

The girls now consist of 3 lots, each lot being 2 groups.

So the boys, after 30 leave, will have to be 2 lots, again each lot being 2 groups: 4 groups in all.

So, 9-4=5 groups of boys departed, and these 5 equal groups totaled 30 boys.

Therefore, 1 group has 6 students.

So originally there were 54 boys (9 groups of 6) and 36 girls (6 groups of 6).

Algebra

Of course algebra is pretty sweet too, just being arithmetic on names.

So, in the first problem, let b be the number of boys at the start, and g the number of girls.

Because there are 3 boys for every 2 girls we know that 2b=3g (think about it for a minute: it’s not the other way around, because “b” doesn’t stand for “boys” – it stands for “number of boys”, and “g” stands for “number of girls”, not “girls”).

After b has decreased by 30 we have b-30 boys and a ratio of 3 girls for every 2 boys.

So, 2g=3(b-30) (again think about it for a minute: it’s still not the other way around).

Let’s do some arithmetic on these names:

2g=3b-90 so 6g=9b-270.

Also, from 2b=3g we see that 4b=6g.

Combining these we see that 9b-270=4b.

Therefore, 5b=270 so b=54.

Then 3g=2b=108 so g=36. Ta-dah!

Notice I carefully avoided using fractional quantities.

Does it feel to you, as it does to me, that the diagrammatic solution and the algebraic solution seem to utilize different parts of our brains?