Computation and the golden mean
Posted by: Gary Ernest Davis on: September 8, 2010
This post is a slight variation on a theme of Cleve Moler, no rx founder of The MathWorks, from the first chapter of his book Experiments with MATLAB.
Cleve uses MATLAB as the computational engine for his computational explorations. This makes sense because Cleve wrote the early versions of MATLAB to do numerical calculations, and the experiments in his book are, to some extent, a showcase and advertisement for MATLAB, suitable for school students and their teachers.
A drawback to using MATLAB is that it costs – currently $99 for US students.
There are many Open Source alternatives to MATLAB, at least for numerical computation.
For this project we will use a computational tool that, while lacking in high level numerical accuracy, is available to almost everyone: a spreadsheet.
If you do not have a spreadsheet on your computer you can use a Web-based spreadsheet at GoogleDocs, or download the freely available Open Office.
Repeatedly applying a function to its own output
In the chapter on “Iteration” Cleve begins by repeatedly applying the function to a number. In fact, to be concrete, he starts by applying the function
at
and then repeatedly applies
to the output. We can think of this schematically as follows:
We can do this easily in a spreadsheet, because a spreadsheet allows us to apply a formula to a previous output:
| Starting value:Â x = | 3 | |
| Number of times    we apply the function F | Output | |
| 1 | 2 | |
| 2 | 1.732050808 | |
| 3 | 1.65289165 | |
| 4 | 1.628769981 | |
| 5 | 1.621348198 | |
| 6 | 1.619057812 | |
| 7 | 1.618350337 | |
| 8 | 1.618131743 | |
| 9 | 1.618064196 | |
| 10 | 1.618043323 | |
| 11 | 1.618036873 | |
| 12 | 1.61803488 | |
| 13 | 1.618034264 | |
| 14 | 1.618034074 | |
| 15 | 1.618034015 | |
| 16 | 1.618033997 | |
| 17 | 1.618033991 | |
| 18 | 1.61803399 | |
| 19 | 1.618033989 | |
| 20 | 1.618033989 | |
| 21 | 1.618033989 | |
| 22 | 1.618033989 | |
| 23 | 1.618033989 | |
| 24 | 1.618033989 | |
| 25 | 1.618033989 | |
We see that after the iteration of the function
the output does not change even in the
decimal place.
A plot of the output versus the number of iterations of the function shows how rapidly the outputs approach the  limiting value:
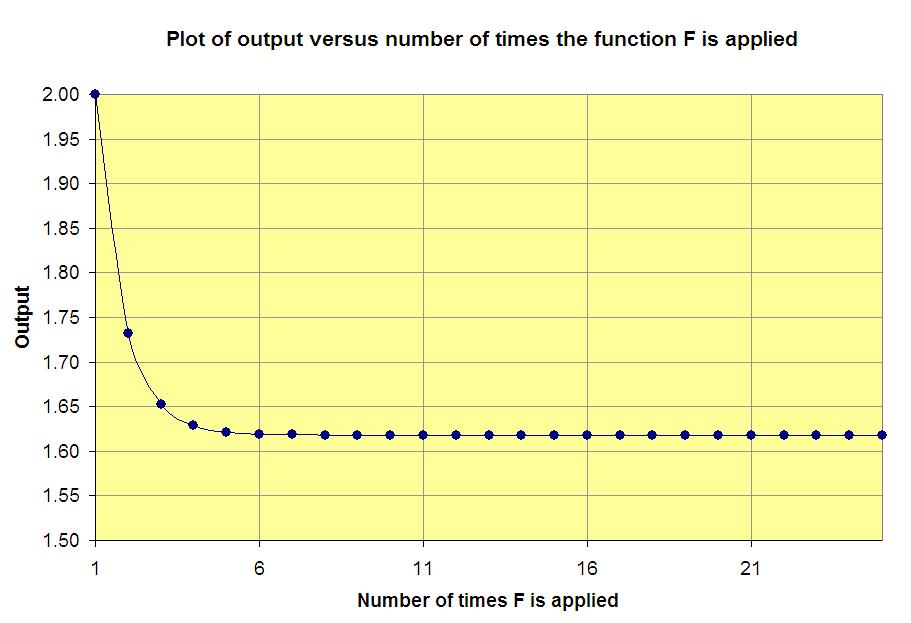
(Almost) any starting value will give the same result
If you experiment with different starting values, other than 3, you will see that repeatedly applying the function to the output leads, after just a few iterations, to what seems to be the same decimal number.
An exception to this is if we choose a starting value less than -1, for example . For then, we would have to take the square root of a negative number (and to do this we would have to use complex numbers, and get into all sorts of hot water about which value of the square root to take).
Cobwebs
When we carry out the iteration above we start with an input value, such as and get an output y-value
.
We than use this output y-value as the new input x-value: . This, in turn, produces a new output y-value:
.
We continue doing this – using the output y-value as the new input x-value -Â until the answer seems to stabilize.
There is a geometric way of seeing how this iteration process takes place, that helps us see how the output values stabilize.
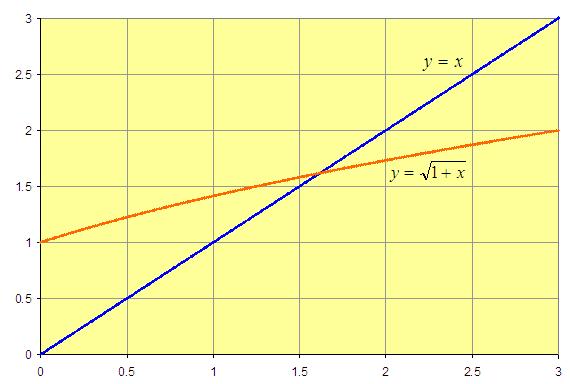
Suppose we start with the x-value .
We draw the graphs of  and
:
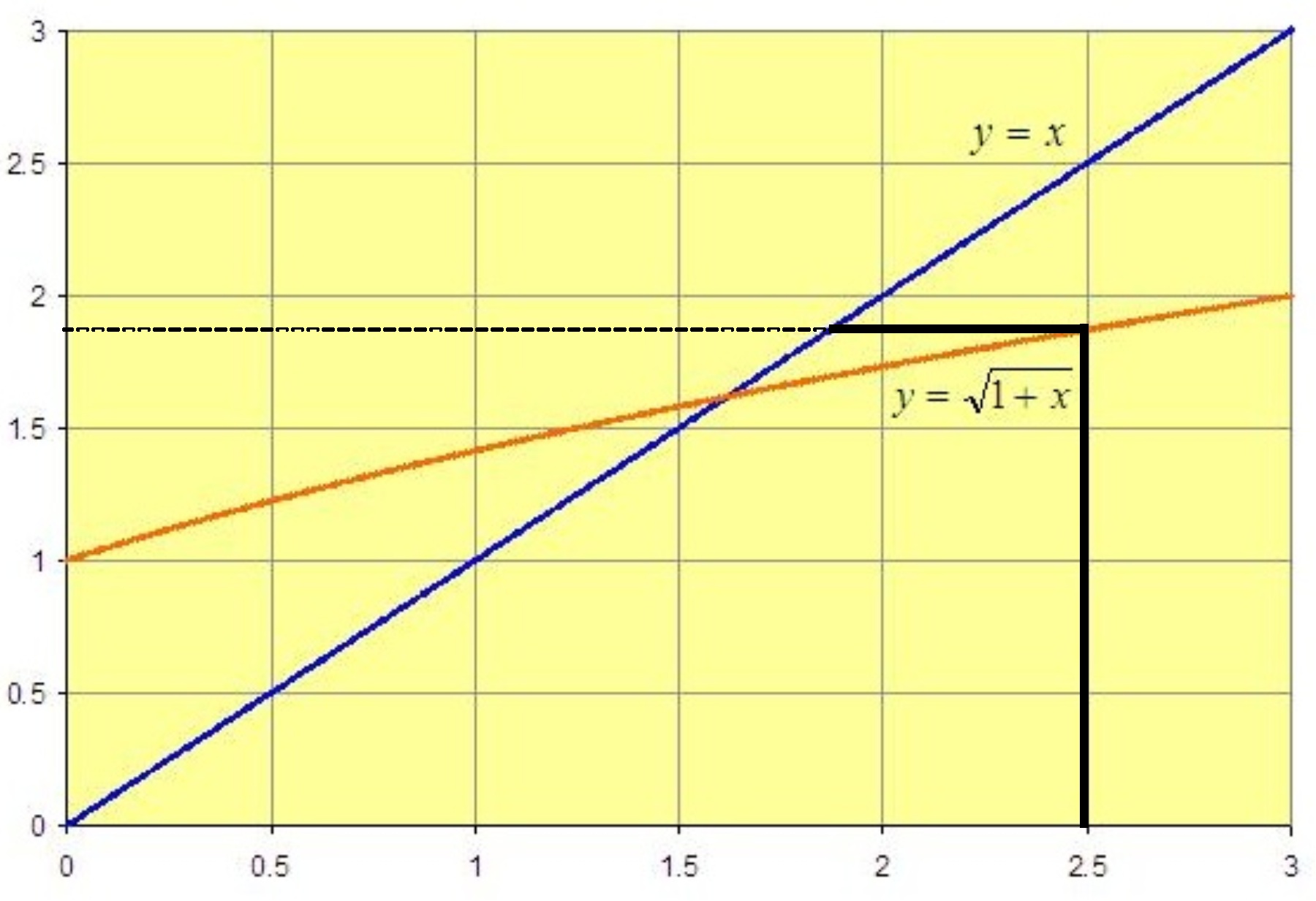
Geometrically, we find the output y-value by drawing a vertical line from the input x-value, , up until it meets the (orange) graph of
, and then drawing a horizontal line from that point to the vertical axis:
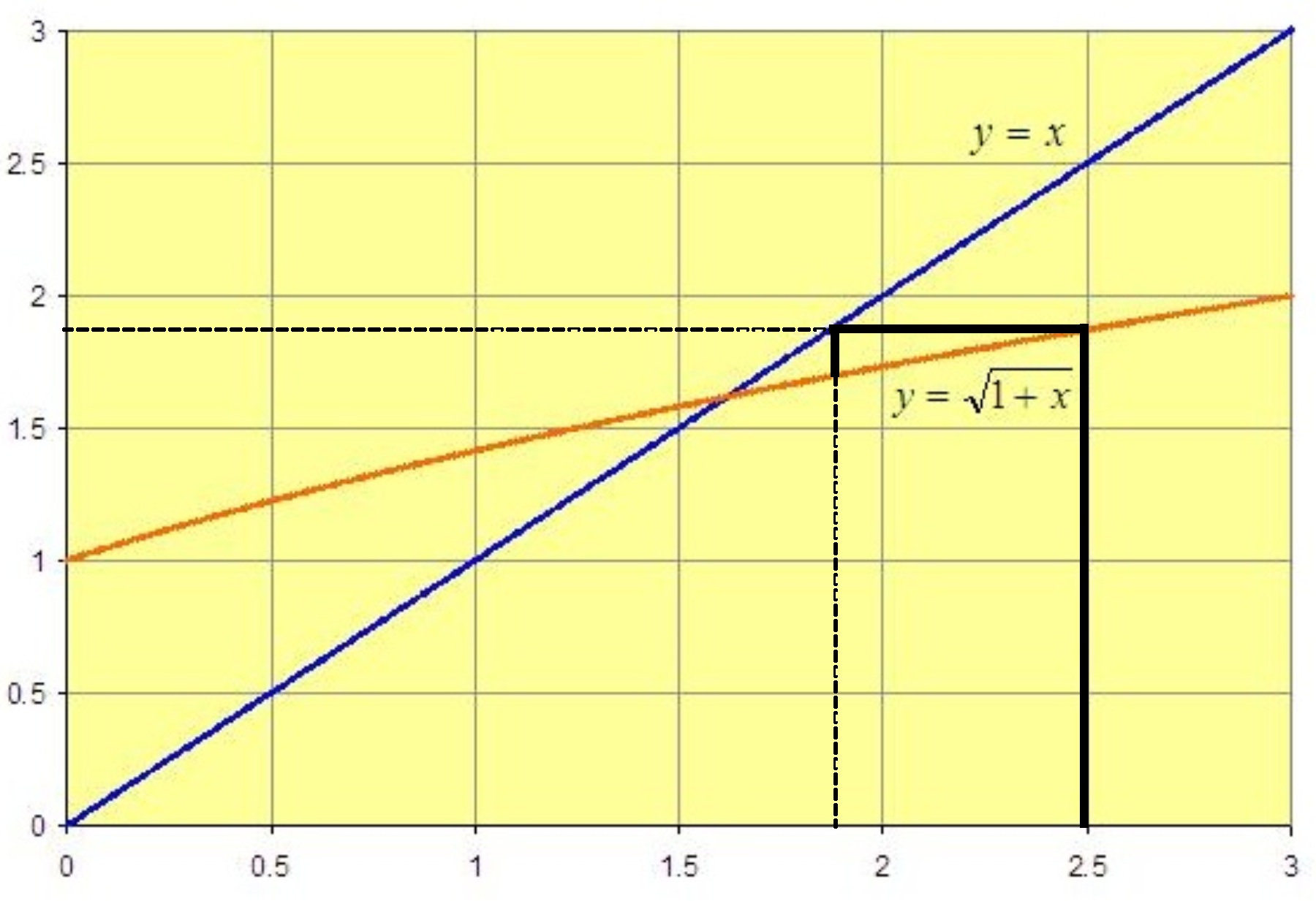
To take that output value as the input value we draw a horizontal line to the (blue) y=x line, and then drop a vertical line onto the x-axis:
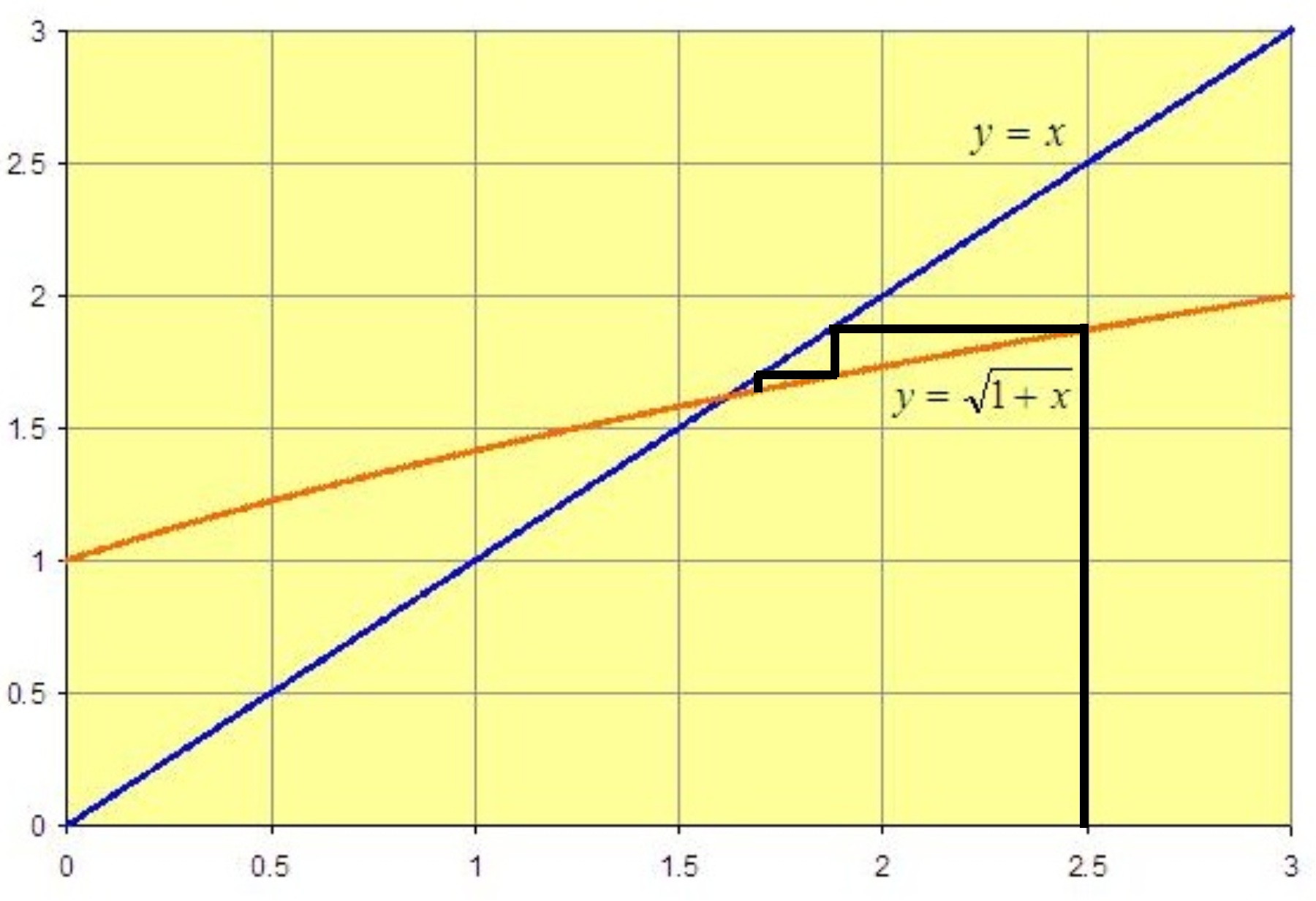
By eliminating the repetitious drawing of lines to the y-axis and the x-axis we get the following cobweb diagram, which shows geometrically what the iterations of the function do to the starting point:
The iterates – the successive outputs – are converging rapidly to a number where
. Using the formula for
we see that the iterates converge to the solution of
. Because this point of convergence is positive, this condition is equivalent to
which tells us that the point of convergence
is the positive root of the quadratic equation:
The quadratic formula tells us that this is .
Continued fraction
Cleve mentions in his chapter on iteration that the equation for the fixed point of the function
also satisfies
as one easily sees by dividing the quadratic expression for
by
.
This double mention of on both sides of the expression
allows us to write:
Applying that idea again we see that:
This makes it look like we should be able to write as an infinite continued fraction:
It is actually relatively easy to see that the fractions we get by terminating this infinite continued fraction at different points do converge to the positive root of .
These first few fractions are, successively:
The numerators and denominators of these approximating fractions should look familiar: they are just successive terms in the Fibonacci sequence
where if is the
term of the sequence then
and
for .
Kool math kids
Posted by: Gary Ernest Davis on: September 6, 2010
I am writing this post as a result of a prompt, a nudge, from some Tweeps, who wrote: “Why does our country often portray math enthusiasts as uncool? Discuss” with a link to:Â “Why is it that other countries celebrate math and science while we often portray them as ‘uncool’?”
This resonated with me because for several semesters now I have been deeply engaged with some seriously cool mathematics undergraduates. I realize, of course, that “cool” is a subjective term [understood deeply only by cool people :)] so in the interests of quasi-scientific research (= your opinons) I want to present you with some really cool mathematics kids, and ask for your feedback on how cool you think they are.
The students I want to present to you, along with some of their cool interests, are all undergraduates at the University of Massachusetts Dartmouth. They all are, or have been, participants in a National Science Foundation funded project designed to stimulate interest in computational science.
Sidafa Conde and Zachary Grant
Sidafa is a mathematics and business major, and Zach is a mathematics major. These two undergraduates work together on Fourier analysis and Fourier approximation of functions.
Sidafa spent Summer 2010 working with a group of undergraduates on Enabling Physiologically Representative Simulations of Pancreatic Beta Cells at the University of Maryland BC Â on the Interdisciplinary Program on High Performance Computing. Sidafa said to me when he returned to Dartmouth MA that other students at UMBC wondered how he knew so much about advanced topics. The answer lies in the stimulating and fun atmosphere that we promote in our program for these enthusiastic students.
Zach spent the Summer working on a research project with his mentor Professor Sigal Gottlieb, and presented a talk on his research – Adaptive Hybrid Trigonometric Polynomial Reconstructions [grant_siam2010presentation]-Â at the annual conference of the Society for Industrial and Applied Mathematics in Pittsburgh. At that talk a professor of mathematics from another university asked Zach to consider applying for graduate school there. Zach was then a sophomore so he had to respectfully decline. Zach’s work with Sigal Gottlieb will likely lead to a significant publication soon.
Sidafa and Zach have presented talks or posters together, and with other undergraduate students, at  Sigma Xi Research Exhibitions, the Mathematical Association of America regional meetings, and at the Massachusetts Statewide Undergraduate Research Conference.
Sidafa and Zach are exceptionally kool math students who we hope will, this Fall semester, go and talk to high school students about their love, passion and achievements in computational mathematics.
Leanne Silvia
Leanne Silvia began as a honors student in our undergraduate computational science program when she was a freshman. This Fall, as a beginning junior she will be presenting her research at the Wolfram Technology Conference in Champagne, IL.
Leanne’s current research project [lsilvia_siam2010poster] – not her first! – Â is devising improved algorithms for finding cliques in simple graphs. The clique problem is NP complete, so if then there is no fast algorithm to solve this problem. Mathematica has in-built algorithms (in Combanitorica) to find maximal cliques. Leanne’s algorithm finds all cliques, and over a certain size of graph, does it faster than existing Mathematica algorithms.
Leanne came to this problem as a result of being in an upper level course on modeling protein-protein interactions. Her algorithm may prove to be especially useful to biologists working in this area.
I think Leanne is one really kool math kid.
Chris Bresten
Chris entered the University of Massachusetts Dartmouth as an honors freshman student. In his freshman year he worked with his adviser Professor Jae-Hun Jung, now at SUNY Buffalo, on the rate of convergence of a parameterized family of quadratic maps to fixed points. This original work has since been published [C. L. Bresten and J.-H. Jung, A study on the numerical convergence of the discrete logistic map, Nonlinear Sciences and Numerical Simulations,14,pp. 3076-3088, 2009.]
Chris has worked on a range of research topics, including cryptography [cbcrypto], random noise generators & image processing.
Chris is now a graduate student in the Department of Mathematics at SUNY Buffalo.
Chris is, and will forever remain, one of the koolest math kids I have had the privilege of knowing.
Adelaide Hopkins
Adelaide is an exceptionally kool math student.
She graduated in 2010, and as an honors student worked on computational aspects of detecting terrorist networks [ahopkins_report].
Adelaide was a mathematics major and became passionately interested in Middle East politics, and terrorist networks in particular. We talked about how she could marry these interests and she came up with a project with her mathematics adviser, Professor Dana Fine, to explore computationally the aspects of terrorist networks.
Adelaide’s research is a fine example of how following one’s passions, however far apart they seem, with appropriate mentoring, can lead to exceptionally cool research.
Adelaide is a gem and a truly kool math kid.
_____________________________________________________________________________________________________________
We have the pleasure of working with these , and other, exceptionally talented passionate students. We mentor them to follow their interests, to talk in class, to present posters and talks at conferences, and to make a difference in the world. Â That’s kool!