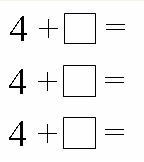Informal induction
Posted by: Gary Ernest Davis on: February 10, 2010
Th University of Massachusetts Dartmouth admits selected students, who do not qualify for regular university admission, into a special program with an extra foundation year.
Here’s the information from the University website:
“UMass Dartmouth offers two alternative admissions programs:
- College NOW
- START
They are intended for those who have completed high school or its equivalent, and who want to and can do university-level work, but whose academic achievements have been hampered by certain social, educational, or economic obstacles.
The university works with applicants to help them find the most appropriate avenue of admission either through regular admissions, or an alternative program such as College Now or START.”
Several semesters ago I was teaching a mathematics problem solving course in the START program. This course was devised by my late colleague Jim Kaput. The course has several aims including introducing students to  college level mathematics in an enjoyable way and increasing their problem solving skills.
Many of the students admitted to College NOW and START are first generation college students of Cape Verdean heritage. Â They have very deep and strong cultural and community ties, but are not especially attuned to an academic culture.
Apart from mathematics , English, and science, students in these programs take a course in study skills.
Among the many problems I set the class was the following:
Imagine a  square grid – same number of rows and columns – where the number of rows (and columns) is a power of 2: 2, 4, 8, 16, 32 ,…
Remove one corner square from that grid:
Is it always possible to tile the  grid with the corner removed by tiles of the following shape:
The class tried various combinations for a grid and, after a short time, found that they could tile a
grid, with corner removed, by L-shaped tiles:
The students struggled with an grid, until a young man, Mathias, declared he had the solution.
As is my custom, I asked him to go to the white board and share his solution with us.
Mathias was a confident, even brash, young man. He began to reconstruct his solution process on the white board, and become a little confused. The other students chimed in with suggestions, until Mathias quietened them, and carefully explained his basic idea:
Split the grid in half horizontally and vertically:
Remove corners from the full grids in the following way:
We know how to tile each of these grids with corners removed:
Put the grids back together again ,and put an L-shaped tile in the empty space in the middle:
 Mathias was very proud of his solution. He waved his hands to indicate the class could applaud, which they did. Mathias bowed and returned to his seat, beaming.
Mathias was very proud of his solution. He waved his hands to indicate the class could applaud, which they did. Mathias bowed and returned to his seat, beaming.
I asked Mathias and the class if they could now tile a grid with a corner removed. Mathias hesitated only slightly before saying that you would do the same thing – split the grid halfway horizontally and vertically  to get 4
grids, which we can tile, after we take away corners. So tile these grids, put them back together and put a single L-shaped tile in the middle.
When I asked why having a power of 2 number of rows and columns was important, a young woman in the class answered that it was because when you split a power of 2 in half, you still get a power of 2.
Mathias had essentially found for himself a  form of inductive construction – an informal inductive proof.
The inductive step is to split a grid in half horizontally and vertically, remove corners from the 3 full
grids, tile each of the smaller grids with corners removed, put them back together and add a single L-shaped tile in the middle empty space (where the corners were removed).
At the end of the class I asked Mathias what he had learned from his solution.
He asked “What I’ve learned?”
I repeated: “Yes. What have you learned from this?”
He thought for a moment, looked me in the eye, and said: ” What I’ve learned is that although we don’t know much, we’re not stupid.”
I think that sums up why we admit young people into these programs. Their  academic achievements have been hampered by certain social, educational, or economic obstacles, yet they want to learn and are capable of learning.
Further comments on induction
The solution to the tiling problem is a stronger statement than saying is  divisible by 3  for
.
This latter statement is often set as an exercise in induction, but, as my colleague Bob Speiser, an algebraic geometer, pointed out it’s a routine consequence of arithmetic modulo 3:
so Â
Counting-on: a basic counting skill
Posted by: Gary Ernest Davis on: February 9, 2010
5 year old Tim’s dad asked him: “Tim, you can see 8 crackers on the table. How many more would you need to have 13 crackers?â€

As he worked on this problem Tim moved his jaw from side to side 5 times, talking very quietly as he did, and then said: “Five”.
What was Tim doing, and what was he counting?
It seems that Tim counted how many times he moved his jaw as he said “nineâ€, “tenâ€, “elevenâ€, “twelve, “thirteenâ€, and so concluded that 13 is 5 more than 8.
In fact, when his dad asked him Tim said that’s what he did.
Tim can count in a way that many 5 year olds cannot. He does not have to always begin counting from “one”.
Tim is at the very beginning stages of learning how to count-on.
He uses body movements, coordinated with saying a number that does not begin at “oneâ€.
He counts his body movements as he does this. Tim has to focus his attention very carefully and coordinate his speech and his jaw movements.
Tim seems like a child who is counting physical objects except that he counts the movements of his jaw.
But Tim is doing much more than that.  He begins saying part of a number sequence, beginning at “nine’ – the point he would have been at if he had counted from “one†through “eightâ€.
What this tells us is that he can mentally extract a number like “eight†from the sequence of counting numbers and begin his counting from there.
Because Tim can begin saying counting numbers from points other than “one†he is at the beginning of being able to count-on.
Children who can count-on – that is, begin counting from a given number – will usually use this ability to figure out a problem such as “8 + ? = 13â€, much as five year old Tim did.
They will also use counting-on to solve addition problems. For example, a child who can count-on will typically answer a question such as “What is 7 and 4 more?†by counting-on from “sevenâ€: “eightâ€, “nineâ€, “tenâ€, “elevenâ€.
At first, children count-on to solve addition problems by starting from the first number presented to them: for 3 + 7 they will typically begin by counting-on from 3. Only later, as they have mastered this aspect of counting-on, will they begin by counting-on from the larger number (7, in this example.)
Tim, and other children who tap their fingers when they count-on, are focusing mainly on body actions. The children make body actions such as tapping, or biting their lips as they count-on. It may be that they do not have visual or other concrete images in their minds. They may be focusing on keeping in working memory the number of taps or bites they are making.
Whichever is the case – focusing on mental images or on real-time body movements – the thing these children are not doing is taking the number names from one: “one”, “twoâ€, “three†… as things to count or to recite.
Children who count-on have made a huge advance beyond being able to count physical objects, even hidden ones. They are flexible with regard to where their counting begins.
Many teachers and adult helpers believe that all children in the early grades of school should be able to count-on, and for those who cannot, the teacher should show them how it is done, by direct instruction.
For example, a grade one teaching assistant, Marie, was working with a small group of children. These children had been assessed by the teacher as the most needy in the class, on the basis of their counting skills. The task for them was to choose a small number of blocks from a container, and say how much more than 4 the total would be. The children had all been given a work-sheet with numbers and totals to be filled in:
Edward, a 5 year old, reached into the container and picked out 5 blocks.
Marie asked him to write 5 in the first box.
Marie already knew Edward would not be able to count the 5 blocks and 4 more without seeing the other 4, so she asked Edward to take out 4 more blocks. She then asked him how many there were in total.
He bunched all blocks together and counted: “one, two, three, four, five, six, seven, eight, nine.†He then wrote 9 after the equality sign.
Edward repeated the exercise, this time choosing 3 blocks from the container. Again he bunched all the blocks together and counted from 1 through 7, before writing his answer. At that point Marie said to him:
“Edward, you are always counting 4 more than what you choose, so just start from 4.â€
“OKâ€, said Edward.
He reached in the container, and took out 4 blocks. He then took out 4 more, bunched them together, and counted from 1 through 8.
Marie stopped him.
“Edward, did you listen to what I said? You can begin counting from 4. Like this: four, five six, seven, eight.â€
Edward nodded his head, reached into the container and took out 8 blocks. He took out 4 more, bunched them together, and counted from 1 through 12.
Marie shook her head in frustration.
Of course Marie was frustrated. She did not know about children’s developmental counting types, and to her, as an adult, it just made sense to count from 4 when you always had 4 to add to the new number of blocks from the container. All she was doing was showing Edward how to do that.
Sadly, for both Edward and Marie, Edward was not yet able to count-on.
Edward needed work on counting physical objects, and then help progressing to being able to count hidden objects he could not see, such as crackers in a box:

Edward first needs to learn to figure problems like: there are 2 crackers on the table and 4 more in the box. How many are there in all?
No amount of telling, in that class period, was going to help him count-on.
Careful assessment of a child is of the utmost importance if an adult is to help that child progress to more efficient methods of counting. A child’s self-esteem rises when an adult takes interest in what they can do, listens carefully, assesses thoughtfully, and then suggests new things for the child to do, at which they can be successful.
Edward was in a situation where Marie, meaning well, was rapidly lowering Edward’s self-confidence with counting.