It IS about the technology: mathematics has computational objects
Posted by: Gary Ernest Davis on: February 2, 2010
I read a lot – particularly on #edchat and #edtech on Twitter – that “it’s about the pedagogy, not about the technology.”
There’s something about this that bugs me in relation to my current mathematical teaching and mathematical experience.
Maybe in language or English teaching the technology is “only a tool”. I want to argue a point of view that, for certain parts of mathematics the technology, the practice and the pedagogy cannot sensibly be separated.
Note I did say “sensibly”. We can, of course, always separate these things. The issue is whether it makes any real sense to do that.
So here’s a few things that come to mind from my recent experience where  the pedagogy does not come before the technology, where the technology is part and parcel of the pedagogy and the experience of doing  mathematics.
Graphs.
By this I mean nodes joined by edges:
When the graphs are small – not many nodes, not many edges – we can calculate quantities associated with them, and work out their relevant features, by hand.
However, when the graphs get big, such as:
or:
we have no choice but to resort to technology to calculate and to discern deeper features- large and small scale – of such graphs.
This is not just a use of technology as a tool, for the reason that our object of inquiry – the graph itself- is presented to us as a computational object. It’s defining features- the nodes and their connecting edges – are given to us as lists in a database. Â We can draw stunning pictures, such as those above, but the results are too complicated for our eyes and brain to comprehend at a deeper level.
Our very object of inquiry is a computational object, so using technology to explore it, to teach about it, to find its properties, is  both necessary and natural.
Statistics.
I am currently teaching a statistics course in which the first descriptive statistics exercise is to ascertain if there is a significant difference between he birth weights of smoking versus non-smoking mothers.
There are thousands of mothers in the data from the study. We could – with much patience and a lot of error – do the laborious calculations by hand. However, the data is presented to us as a computational object. It is a list of birth weights and smoking indicators. As such, the data naturally presents itself as something to be addressed through technological means.
Most students are using R, some Excel. Again, the technology is not “just a tool”, useful but not essential. Rather, the technology both educates and provides a natural point of engagement with the data.
The pedagogy, practice, and technology are not separate, nor sensibly or easily separable.
Differential equations
For the first 3 weeks students are working on modifications of Newton’s law of cooling and could do all calculations and drawings of graphs by hand. They do not, because I prefer to get them used to using professional grade tools such as MATLAB. That is a matter of choice, not of necessity.
In a couple of weeks time students will be tackling the numerical approximation of non-linear systems of differential equations. Here they need to carry out many thousands of difficult calculations, many times over. Once again, the object of inquiry is presented to us as a computational object, so learning about it and working with the technology are one and the same thing – not easily or sensibly separated.
Biological modeling
This class is working through a book on protein-protein interactions. The data about these interactions are specified in large data-bases. Again the objects of our inquiry are presented as computational objects, so learning about them is initially linked with the technology we use. The technology is a tool that is not easily or sensibly separated from the learning or the study of these objects.
_______________________________________________
You may say that this is all very well at the undergraduate level but in school we do not deal with such complicated mathematical objects.
With that statement I agree. However, Â we can stick to mathematical issues or problems where there only small graphs, small data sets, simple differential equations, and we can avoid large chunks of biological data altogether. We can do that, but it’s not how much of the scientific, technological, engineering and business world is going these days.
Computational objects are becoming more and more common.
Twitter itself is a computational object. How many of us have never looked up our score on Twitter Grader?
For computationally presented objects the use of technology to examine them, to learn about them, is essential.
It IS about the technology for these computational objects, and mathematics is rapidly developing an increasingly computational face.
Students whose mathematical learning is separate from the use of technology will be increasingly ill-equipped for the modern workplace.
Algebra as arithmetic on names
Posted by: Gary Ernest Davis on: February 1, 2010
Arithmetic on names
Algebra is powerful because it allows us, among other things, to do arithmetic on the names of variables or unknown quantities and find specific numerical values for those variables or unknowns.
If, as some people assert (wrongly, in my view) that mathematics is only a language, then it is a very peculiar language indeed. In what other language can you carry out arithmetical operations on names?
A problem
Here is, in my opinion, a lovely example of how  simple algebra allows us to find a complete and rigorous answer to what seems like a difficult problem.
The problem is this:
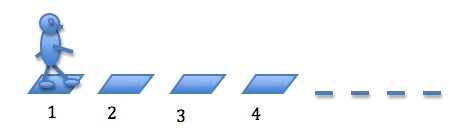
Imagine you are standing at the beginning of a very long path, made from stone steps, as shown in the drawing, below:
You have a fair coin in your hand and you flip it. If the coin lands heads up you take 1 step forward; if it lands tails up you take 2 steps forward.
Keep doing this until you either land on step 20, or else you pass step 20.
Record whether you did or did not land on step 20.
Go back to step 1 and do this over.
Do it over many times.
With what probability – exactly or approximately – will you land on step 20?
A physicist tackles the problem
Here is how a smart physicist friend of mine answered this question:
“Let’s see” he said. “By step 20 the transient behavior has died out, so there’s about the same probability of landing on any given step. That probability must therefore be the reciprocal of the expected value  so the probability is approximately
.”
Inventing some names
You might wonder why step 20, and not step 30, or step 100? So let’s ask with what probability would we land on step n where n could be
This probability is what we do not know, and wish to find.
Algebra begins by naming unknowns and variables, so let’s name the probability of landing on step n. We could call it “Brian” or “Shirley” but how about simply “p” for probability?
But, if p is the probability of landing on step n, shouldn’t we incorporate into the name something that tells us which step we’re at? Say, call this probability ““? After all,
 will presumably be different, so we don’t want to give them all the same name, p.
Some facts about these names
What do we know about this probability?
Experimenting with many coin tosses will soon convince you that what happens early on does not matter, and the only thing that is important for step n is whether you do, or do not land on step n-1.
How can you NOT land on step n?
The only way is to land on step n-1 and throw a tail, which skips us over step n and onto step n+1.
So the probability of NOT landing on step n is the probability of landing on step n-1 and then throwing a tail. Nothing that happened before step n-1 matters.
Arithmetic on the names (= algebra) leading to a pretty picture
Here comes some arithmetic on the names of these probabilities.
The probability of landing on step n is so the probability of NOT landing on step n is
.
The coin is fair so it lands tails up the time.
The tosses of the coin are independent, so the probability of not landing on step n is the probability of landing on step n-1 and then throwing a tail.
In terms of names, this says that .
Because these are names of numbers, we can do more arithmetic on the names, and so express .
Do the probabilities become approximately the same as n increases, just as the physicist asserted?
If they do then for large n, say , we will haveÂ
so
.
Doing some more arithmetic on the name we see that
so
.
So IF – and it might be a big “IF” – the probabilities become approximately equal then they must get closer to .
Do they, in fact, get closer to ?
To figure this out, let’s look at the difference between the probability of landing on step n and .
In terms of arithmetic on names, this is .
What do we know about this?
Well, we know .
Doing some more arithmetic on these names we see that .
Let’s give the difference between the probability of landing on step n and a name: let’s call it “error(n)“.
Our arithmetic on names tells us that error(n) error(n-1).
So at each step the error changes sign and becomes half as big.
In other words the error approaches 0 very fast – exponentially fast -Â changing sign as we go from one step to the next.
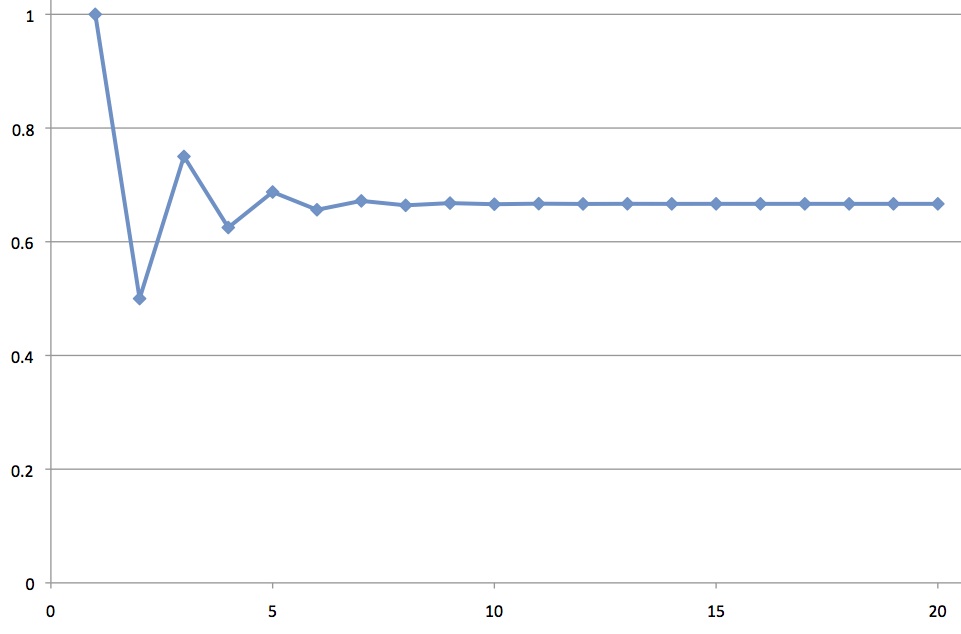
So the probability of landing on step n does indeed approach – exponentially fast in fact – so that by step 20 it is very nearly
.
A plot of versus n shows this clearly:
Amazing that from the one idea of how we could NOT land on a given step, we can do simple arithmetic on the names of probabilities and come up with this nifty graph.
Algebra has its uses (especially for those of us not as insightful as my physicist friend) !
Similar problems
This problem was originally posed to me with the person throwing a 6-sided die to determine how many steps to move forward (the number of dots on the face of the die that lands up).
For this problem there are more cases to consider how not to land on step n, for large n, but otherwise the reasoning is the same.
If you absorbed the physicist’s argument then you might argue that the answer in this case would be the reciprocal of , namely
, and you would be right.
An analogous argument will show that for a k-segment spinner (see the picture, below), with numbers all equally likely, the probability of landing on step n, for large n, is approximately Â
.
For example, for a 3-segment spinner the probability of landing on step n, for large n, is approximately .