Some stubborn problems associated with the number 3/2
Posted by: Gary Ernest Davis on: December 4, 2010
Fractional parts of powers of 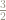
The powers of increase exponentially:
However, if we keep only the fractional part of – that is,
– quite a different picture results:
The first few of these numbers are 1/2, 1/4, 3/8, 1/16, 19/32, 25/64, 11/128, 161/256, 227/512, 681/1024, 1019/2048, 3057/4096.
Despite much study, there are things about this sequence of fractional numbers that are not known.
Equidistribution
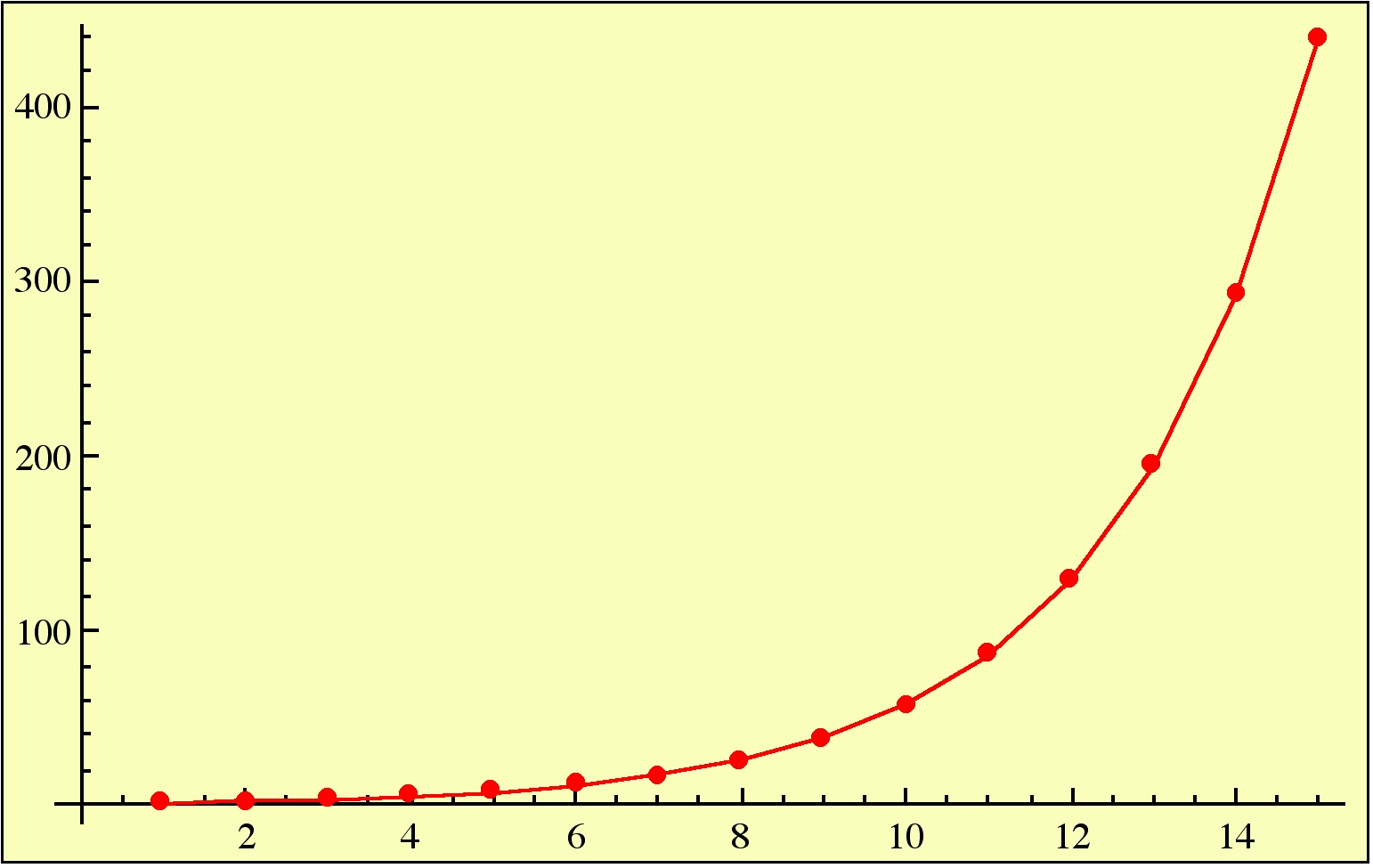
If we take an interval of numbers such as and for each
count how many times
lies between
, will the ratio of the number of times to
approach the length of this interval – namely, 0.1 – as
increases?
For example, in the second picture above, it is true that for exactly 101 values of we have
, and
.
This property, when true for any interval is known as equidistribution of the sequence of numbers
.
Back in 1914 Hardy & Littlewood proved that for “most” numbers the numbers
are equidistributed in the interval
.
(Hardy, G. H. and Littlewood, J. E. “Some Problems of Diophantine Approximation.” Acta Math. 37, 193-239, 1914)
It is not known if is one of those numbers.
Density
An equidistributed sequence of numbers must land in every interval
because the
must land in
the right number of times.
The property of landing in each interval at least once is called density of the sequence
.
It is not even known if the sequence is dense, let alone whether it is equidistributed.
A powerful, but stubborn, inequality
It is widely believed, but still not known, if the fractional part of , namely
, satisfies the inequality:
for all
………………..(*)
If this inequality is true then a famous problem of number theory – Waring’s problem – is known to be true.
The inequality (*) seems innocent enough, yet no-one to date has been able to prove it is true.
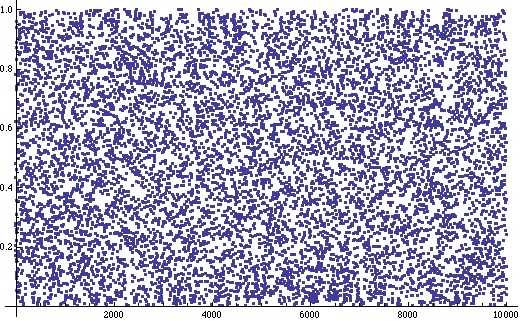
If (*) is true and we plot versus
we should never get a negative value.
A plot of the first 10,000 of these numbers looks as follows:
Of course it’s hard to see from this plot how close to 0 the values of get.
There are values of for which
is smaller than
for all previous
.
The first few of these values of and the corresponding values of
are:
| Values of n for which F(n) is less than any previous F(i) | F(n) |
| 5 | 0.168945 |
| 14 | 0.0529218 |
| 46 | 0.0317909 |
| 58 | 0.0297681 |
| 105 | 0.0144072 |
| 157 | 0.00725365 |
| 163 | 0.00449855 |
| 455 | 0.00314395 |
| 1060 | 0.00110873 |
| 1256 | 0.000564205 |
| 2677 | 0.000363945 |
| 8093 | 0.0000809868 |
| 28277 | 0.0000604566 |
| 33327 | 0.0000549506 |
| 49304 | 0.00000736405 |
x
Is this a “good” problem?
The inequality (*) is intriguing, and if you can prove it you will undoubtedly become (mathematically) famous.
But it is it a good problem to work on?
A graduate student should not work on this problem because the chances of getting anywhere new are very slim.
A professional mathematician might play with it, in the hope of having a few ideas.
School students might also play with it in the hope of getting a sense of what the problem means and why it is hard: there are very few such hard problems in mathematics, with such strong implications, that are so easily stated.
A good starting point for school students to experiment is with the the fractional part of the powers of .


December 10, 2010 at 5:13 pm
You asked on Twitter: Is there an x* > 0 such that 1-(3/4)^x-frac[(3/2)^x ] > 0 for all x > x* ? I think there is no such x*, but I don’t think I can rigorously prove why… This is assuming that x can be any real number, and is not restricted to integers.
My reason has to do with the nice continuous nature of f(x) = (3/2)^x. All that frac[(3/2)^x] does is translate a section of f(x) = (3/2)^x down.
For x from negative infinity to 0, you translate down 0 units. For x from 0 to [log (2)/log (3/2)], you translate down 1 unit. Since f(x) = (3/2)^x is continuous everywhere, then (3/2)^x gets as close as you want to 2 as x approaches [log (2)/log (3/2)]. And, it gets there faster than 1-(3/4)^x gets close to 1, since the slope of 1-(3/4)^x is decreasing, whereas the slope of (3/2)^x is increasing.
The same thing happens on every interval, and the intervals get smaller and smaller as x gets bigger, so it becomes even more frequent that frac[(3/2)^x ] “crosses” 1 – (3/4)^x
Can anyone help me formalize that?