Spotting patterns and finding explanations: Dijkstra’s fusc function
Posted by: Gary Ernest Davis on: May 18, 2011
Edsger Dijkstra named the integer valued function, fusc, of a non-negative integer variable, as follows:
,
,
and
Dijkstra’s writings on fusc can be found at the Edgar W. Dijkstra Archive (EWD 578).
The values of fusc can be computed in any decent programming language (one that has a built-in routine for recognizing odd and even integers – otherwise one has to define such a routine, or include it in the definition of fusc).
Here is a simple Mathematicaâ„¢ definition that allows us to compute fusc easily:
fusc[0] = 0;
fusc[1] = 1;
fusc[n_] := If[Mod[n, 2] == 0, fusc[n/2], fusc[(n – 1)/2] + fusc[(n + 1)/2]]
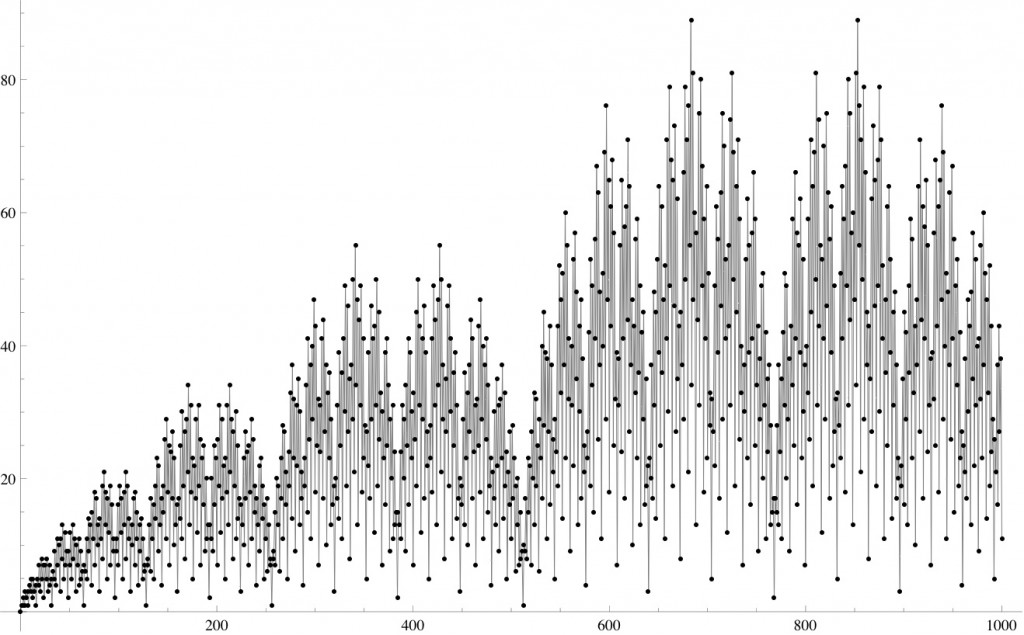
Here are the first 100 values of fusc:
0, 1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4, 1, 5, 4, 7, 3, 8, 5, 7, 2, 7, 5, 8, 3, 7, 4, 5, 1, 6, 5, 9, 4, 11, 7, 10, 3, 11, 8, 13, 5, 12, 7, 9, 2, 9, 7, 12, 5, 13, 8, 11, 3, 10, 7, 11, 4, 9, 5, 6, 1, 7, 6, 11, 5, 14, 9, 13, 4, 15, 11, 18, 7, 17, 10, 13, 3, 14, 11, 19, 8, 21, 13, 18, 5, 17, 12, 19, 7, 16, 9, 11, 2, 11, 9, 16, 7
and a plot of versus
for
:
Spotting a pattern
Among other properties of fusc, Dijstrka noticed that is a multiple of 2 exactly when
is a multiple of 3.
For example, we see that for multiples of 3 up to 99, the value of fusc is a multiple of 2:
| n = multiple of 3 | fusc(n) |
| 0 | 0 |
| 3 | 2 |
| 6 | 2 |
| 9 | 4 |
| 12 | 2 |
| 15 | 4 |
| 18 | 4 |
| 21 | 8 |
| 24 | 2 |
| 27 | 8 |
| 30 | 4 |
| 33 | 6 |
| 36 | 4 |
| 39 | 10 |
| 42 | 8 |
| 45 | 12 |
| 48 | 2 |
| 51 | 12 |
| 54 | 8 |
| 57 | 10 |
| 60 | 4 |
| 63 | 6 |
| 66 | 6 |
| 69 | 14 |
| 72 | 4 |
| 75 | 18 |
| 78 | 10 |
| 81 | 14 |
| 84 | 8 |
| 87 | 18 |
| 90 | 12 |
| 93 | 16 |
| 96 | 2 |
| 99 | 16 |
Equally, for values of up to 100 that are not multiples of 3,
is not a multiple of 2.
Explaining a pattern
This empirical observation requires explanation.
Mathematics thrives on spotting and explaining patterns, especially unexpected patterns, for which there is no immediate reason why they should hold.
To begin looking for a reason for this empirical observation let’s assume that is a multiple of 3.
is either even or odd, so let’s assume first that it is even.
Then for some non-negative integer
.
This gives us .
Now when is a smaller multiple of 3 than is
, so if we assume, inductively, that for all smaller multiples of 3 we already know the value of fusc is a multiple of 2, then we know that
is also a multiple of 2.
What if is a multiple of 3 and is odd?
Then for some non-negative integer
, so
Now, are smaller than
, so we can assume we already know their fusc values, but because these numbers are not multiples of 3, we can assume that we already know their fusc values are not multiples of 2.
In other words, we already know that is odd and
is odd, so their sum is even, and therefore
is even.
This reasoning tells us:
If is a multiple of 3 then
is a multiple of 2 ………… (*)
What if is not a multiple of 3?
Can we reason, as the evidence suggests, that is not a multiple of 2?
If is not a multiple of 3 then
or
for some non-negative integer
.
We first consider the case .
is either even or odd, so let’s assume first that it is even.
In this case is odd so
.
Because is smaller than
and is also not a multiple of 3, we can assume that we already know
is not a multiple of 2.
Therefore, in this case, is not a multiple of 2.
Now consider the case where is odd.
In this case is even so
.
In this sum we can assume we already know the values of and
and that
is even while
is odd.
Therefore is odd.
This deals with the case when . The case
is dealt with similarly.
So we have established:
If is a not a multiple of 3 then
is not a multiple of 2 ………… (*)
and combining (*) and (**) we have:
is a multiple of 2 exactly when
is a multiple of 3 ………… (***)
The basis of this reasoning is induction. Because we calculate fusc recursively we can assume, when calculating, that we already know properties of
for values
.
The induction needs a starting point, just as does the calculation of values of fusc, so we need to check these assumed properties are true for (which they are).
Explorations
Dijkstra raised the question of when is divisible by 3. Such divisibility questions do not have clear and simple answers, yet lead into deeper and interesting explorations.
The first few integers for which
are 5, 7, 10, 14, 20, 28, 40, 56, 80, 112, 160, 224, 320, 448, 640, 896, 1280, 1792, 2560, 3584
Show exactly when
.
5 Responses to "Spotting patterns and finding explanations: Dijkstra’s fusc function"
I love the plot to 1000. Very fractal!
You can get a lot more insight into these properties if you look at the relationship between fusc and the Calkin-Wilf tree and the hyperbinary representations of integers. http://mathlesstraveled.com/tag/hyperbinary/ has a lot of good stuff.


May 18, 2011 at 3:52 pm
Very cool stuff. Thanks for introducing me to the “fusc” function–I teach recursion and induction in my Math Research class, and I’m always looking for new material.
I, too, find that the best way to get students to the core ideas of recursion and induction is by making them get their hands dirty by experimenting and playing around with sequences, as you’ve done here. Another great feature is the potential for students to create their one “fusc-like” sequences!