The curious case of the number 3435
Posted by: Gary Ernest Davis on: April 17, 2011
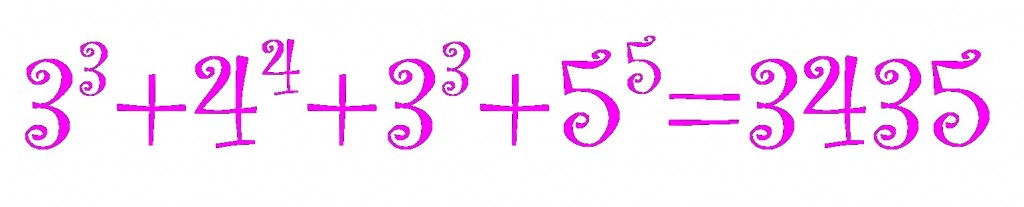 The (base 10) number
The (base 10) number has the curious property that
It shares this property with since
.
What makes even more curious is that it is the only number other than
that has this property.
To prove this we need to talk a little more exactly about what is this property.
The Münchausen property
Suppose is a positive integer and $latex d_k, see ldots d_1, patient d_0$ are the base 10 digits of n.
This means – a fact every elementary teacher of mathematics tries to get across to students when teaching place value – that
So given that (base 10) we form a new number:
The property we are interested in – sometimes called the Münchausen property – is that .
So we see that .
We will now see that there is no other positive integer for which
.
But first, store a little excursion into properties of the function .
Some properties of 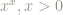 and a convention for
and a convention for 
We should have discussed what happens if a digit of the positive integer is
: because, then, we have to assign a value to
.
There is no magic way to decide how to assign a value to – we will use the continuity of the function
for
:
Because the limit of as
approaches
with
is
we assign the value
.
There is nothing magic about this – it just turns out convenient for our purposes here to have .
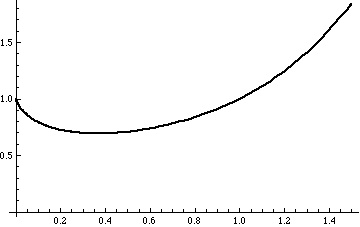
We can see the initially decreases as
increases, reaches a minimum value, and then increases.
We can see this from the derivative of
, which we can calculate by first taking (natural) logarithms:
so
and therefore
This is negative for and positive for
.
So, for non-negative integer values of the function
is non-decreasing: in fact, apart from
, we have
for all positive integers
.
The number of digits of a positive integer
For a positive integer the number of (base 10) digits of
is the floor of
, the largest integer less than, or equal to,
.
This means that the number of digits of is less than
.
An inequality for 
If the base 10 digits of the positive integer are
then:
for
- The number of digits of
is
So,
This says that cannot grow too big in terms of the number of digits of
.
An inequality for large 
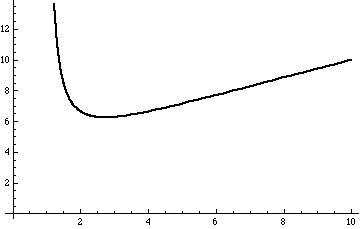
We look at the behavior of the function :
The derivative of is
and this is positive for
.
So, for we have:
x
In other words, for we have
Positive integers  Â cannot be equal to
 cannot be equal to 
x
If is too big – for instance,
– then
cannot be equal to
.
The reason is that for we have
while
So we search through all positive integers up to and find no integers
with
other than
.
Variation on this theme
Suppose instead of forming as we did, we move the digits forward, with the first digit
moving around to be last: in other words, we form a new number
.
Do we ever have ?
Well, yes: we do for because
and
What if we move each digit forward two (with the first two cycling around to be be last and second last)?
References
van Berkel, D. (2009) On a curious property of 3435. Retrieved from arxiv.org: On_a_curious_property_of_3435 [This article provides the argument I have described in this post]
Perfect digit-to-digit invariant Wikipedia.org [In this reference another number is counted as a Munchausen number due to their using the convention 0^0=0]
8 Responses to "The curious case of the number 3435"
You have a small typo in your last sentence: “… due to their using the convention 0^0=1”. Their convention os “0^0=0”, not “0^0=1”.
In the Wikipedia case, the 0^0 = 0 is what qualifies solely ‘0’ to be a Munchausen number. It in no way qualifies that 438579088 to be a Munchausen number. At the same time, the definition merely asks for a number to satisfy ‘n = n*’ to be a valid Munchausen number, in which case, if you suggest that a method of proof does not say so, then the method of proof is obviously flawed (again, which is the not the case). And I say so, because the only conclusion your proof arrives at is that, any n, such that n > 2×10^10 cannot be a Munchausen number and then you go ahead to make an argument that the only number between 1 and 2×10^10 which is a Munchausen number is 3435. The post-conclusion is wrong and is not in any ways affected by how you chose to define your function at a particular discontinuity.
This is so amazing. I wonder what other properties 3435 has?
Wow, that’s fantastic :) While I’m sure this is a relatively simple example, it’s still cool to see a combination of mathematical logic and computing power working in symphony.

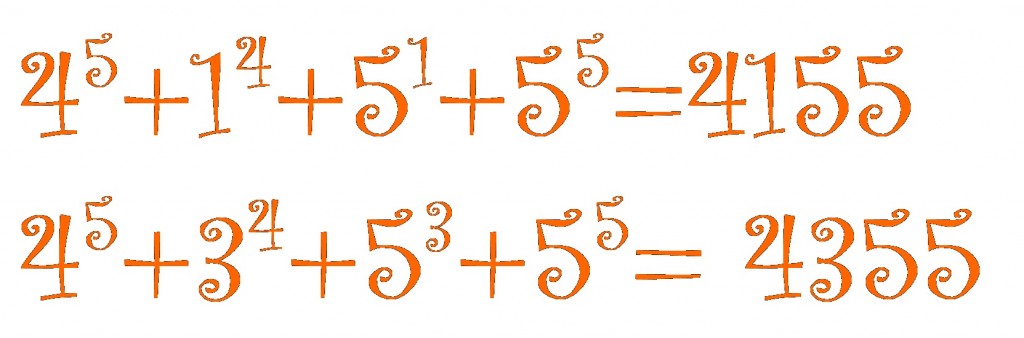

April 23, 2011 at 10:13 pm
You link to Wikipedia, which gives 438579088 as another Munchausen number. Did you even read it?
April 23, 2011 at 10:50 pm
Yes, I did read it.
You will see that there they choose to define 0^0=0, which is how this other number comes to be counted as a Munchausen number.
I explained how for the proof in the post I was taking 0^0=1 and why I was doing that.